一、正确使用单位的词头
在论文中，计量单位在使用过程中必须大小适中。例如长度单位“米”，在天文测量中用以表示星际距离显然太小了;若用“米”表示原子的直径，则是大得不可思议。然而，同样是“米”，加了词头以后，则可大可小，能应用在所有长度测量中。用pm (10-12m) 可以测量原子核，而用Em (1018 m)则可以测量银河系了。
SI规定的词头有16个，它们与几乎所有的(不包括非十进)法定计量单位构成的组合仍是法定计量单位。词头都是十进的，其使用有很多规定:
1、选用SI单位词头的倍数或分数单位，一般应使量的数值处在0.1 ~ 1000的范围内。如果超出这个范围，应使用词头限制。
当然，并不是所有场合都要使带有词头的量值处在0.1 ~ 1 000的范围内。有时，可以根据习惯处理。如在机械制图中，一般以mm为计量单位，即使量的值不在0.1 ~ 1 000的范围内，一般也不换算成带倍数或分数词头的单位。
2、有些非Sl计量单位，可以按习惯用SI词头构成倍数和分数单位，但对于摄氏度(°C) 和非十进的单位不得使用词头。这样的单位还有:时间单位“分(min)”、“时(h)”、“天(d)”，平面角单位“秒(")”、“分(')”、"度(°)"，旋转速度单位“转每分”(r/min)，长度单位"海里(nmile)"、 速度单位“节(kn) ”等。除了这10个单位之外的法定计量单位，均可使用词头。
3、不得使用重叠词头。在一个单位中不能使用两个或两个以上的词头。例如，10-9m， 过去常有人写为mum (毫微米) 10-12F常写为祆F (微微法)。按新的规定，这些写法和读法都是错误的，应改为nm (纳米)和pF (皮法)
4、凡是由词头和单位构成的倍数和分数单位，都是一个整体。
因此，在由这些单位构成乘方时，不必再加括号，如cm表示立方厘米，而不是厘立方米。
5、由法定计量单位构成的组合单位在加词头时必须遵循以下原则:
(1)对于通过相乘构成的组合单位，词头加在第一个单位之前。
(2)通过相除构成的组合单位，词头通常加在分子上，但若分母是长度、面积或体积单位时，可按习惯在分母上加词头。
(3)分子分母一般不同时使用词头，但对kg这个单位应作特殊考虑。由kg单独构成单位时，认为带有词头，加词头时应遵循3，但与其他单位构成组合单位时则不认为带有词头。
这需要注意，词头不是数词。按规定，SI词头仅用以构成十进倍数或分数单位，不能作为数词单独使用，如不能写为4M。
二、数值换算
我们在收集资料的时候，有时会收集到一些使用非法定计量单位的文献。由于单位的改制，一些经典理论中的公式、系数都将发生改变，从而产生了数值换算的问题，如从英制到SI等。这在引用外文资料时经常遇到，如果不考虑单位制不同而直接使用，则很可能造成引用失误。
常用的数值换算方法有两种:
其一，按单位关系代入。例如，“英尺/公斤力.℃” 换算为“米/牛.开”，可采用下列步骤:
1ft=0.3048m,1kgf=9.8N,1℃=1K
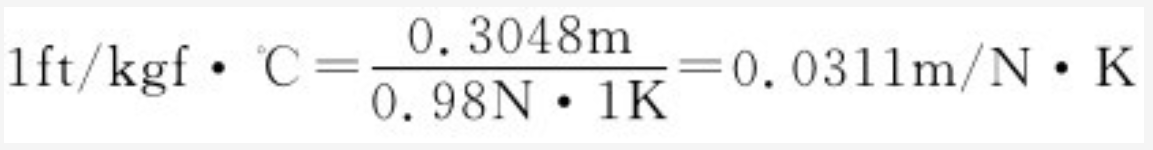
其二，乘以等于1的单位比。还是上例:
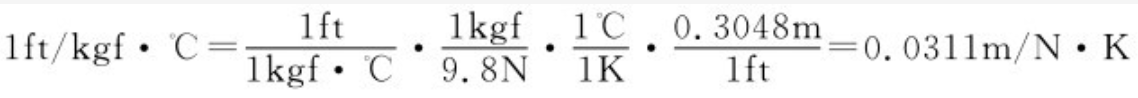
按上述两种方法。可对所有的非法定计量单位进行换算。
不过，在单位换算过程中，需要注意以下问题。
1、数值方程中系数的换算。在单位变换时，数值方程中系数也要进行相应换算。否则，方程将不成立。在弓用过去的经典着作中的公式时，这是经常遇到的问题。
设已知公式为{Q}sl=K{A}sI{B}SI,求不同单位时公式{Q}q=K {A}a/{B}b中的K。根据量值的不变原则，可知:
由此得：
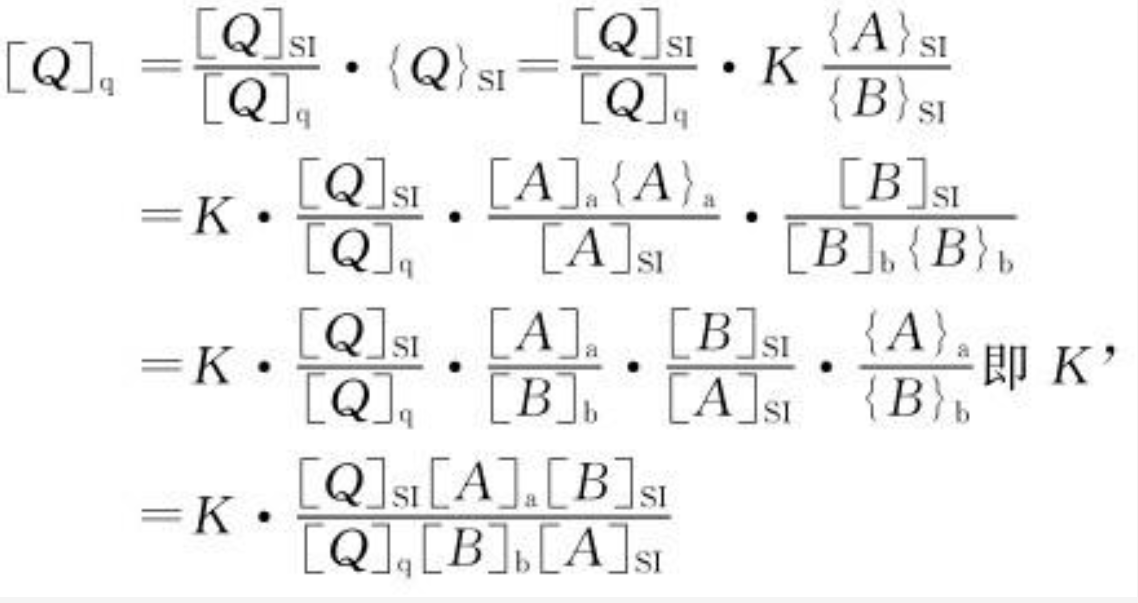
反过来，得：
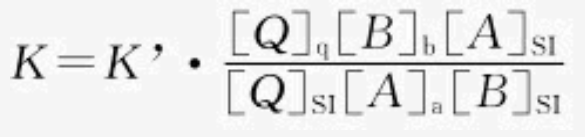
2、极限值的变化。参考文献中的数据范围，在单位变换后也将发生变化。如果数据极限值为准确值，换算后也要求用准确值，不能修约(四舍五入) ;如果数据极限值是近似值，可以按规定修约。
极限值包括最大、最小值。对极限值的修约，只能使修约后的值处在原取值范围内，即对最大值的修约结果只能小于原来的值，而对最小值的修约结果只能大于原来的值。这比较容易理解，否则会使数据超限。
3、单位变换中数值的有效性。数值换算中，经常遇到有效位数不同的情况。很多作者采取的处理方法是:如果是有限小数，直接保留所有小数位，或按换算前的小数位确定换算后的小数位。如果是无限小数，则按其他数据的小数位来保留相同的小数位。这其实是很不严谨的。正确的方式是，有效位的确定应使两个数值的相对精度处于同一量级，即换算前数值的有效位所反映出的相对误差与换算后数值有效位所反映出的相对误差大致相当。
设有两个数M、N,其有效数前两位分别是M0、No (四舍五入)，且Mo < No, M、N的有效位数分别为m、n。 如果（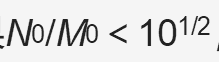
），按n=m确定有效位;否则，按m=n+ 1确定有效位。
例如有一数值1.56，在单位换算后变为0.082764。如何确定0.083164的有效位数呢?在这两个数中，前两位分别是16、83 (已作四舍五入)，因而可设No=83, Mo=16，进而逆推出M=1.56, m=3。
因为，（
）所以两个数值的有限位数之间的关系为m=n+1。而m=3，故n=3-1=2。即0.083164的有限位应保留2位，即修约为0.083。
这一思想不仅用于单位换算，也可用在科学研究中的数据处理上。
三、公式图表及运算中的单位形式
公式是量方程，本身包含单位，因而不必专]指明各物理量必须采用什么单位。带有系数的公式，按上文所述的原则将系数换算成法定计量单位中的系数就可以了。
在运算过程中，要注意使等式两边相应，即"量值=量值”。论文中经常出现的错误是，为了方便，中间的运算过程往往不加单位，而在最后的结果处加单位并用括号括起来，这是不规范的。因为计算过程中若不加单位，表示的仅是纯粹的数值，而结果加单位则变成量值，纯数与量值是无法相等的。
对于不是一个系统中的单位的量值，不能使用等式，而只是相当于（
)。如某像点误差为10um，相当于1/2个像元， 表示为（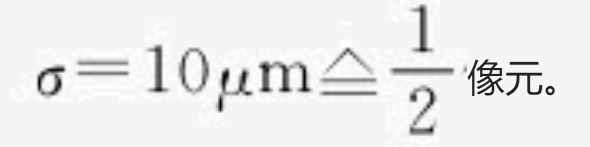
）
在图表中的单位及物理量的表示应注意使所表达的形式与所表达的内容相应。在表格中，表头一般表示物理量及单位，形式如Q [Q]，而表中内容一般为纯数，不写单位，这是错误的。表头也应表示成纯数形式方可与内容相应。由Q={Q} [Q]，可推出{Q}=Q/[Q]，即表头应表示为Q/ [Q]的形式。表1的表示是正确的。
表1
还有一种表达方法，是在纯数后直接逐一加注单位， 形式为{Q} [Q]。该方法一般在运算过程中使用，这里不再赘述。
图中的处理原则与表格中相同，见图1-1、 图1-2。
图1-1
图1-2
有一点需要注意，社科论文中经常用图形表示数据的年际变化，如GDP在各年的变化，纵坐标表示“GDP数值” ，横坐标表示“年份”，如果量的名称标注为“时间”则错误。正确的标注应该是“年份”，无单位。
四、量和单位的使用与表示
量和计量单位可用于定义和表述，但要注意使用准确，不能弄错。
在一般性的叙述中，使用量和单位也要注意准确、恰当，对容易混淆的物理量要注意区分。如压力与压强，在物理.上这两个概念很明确,而工程上则不同。一般工程上讲的大气压力、蒸气压力、压力表等中的压力实质是压强，应使用压强的单位。类似的还有质量、重量及重力。对已经废止的公制和厘米克秒制中有专门名称的单位不能使用。
在量和单位的使用过程中，还有其他一些要注意的问题:
1、单位符号的先后次序。词头一般在前，其他遵从习惯。如温度、时间的符号-般在后，当温度、时间同时出现时，温度符号放在最后。
2、单位不存在复数形式，如“千克”不能记为kgs.
3、单位不能加形容词，任何需要区分的物理量只能在量的符号上区分，而不能在单位符号上区分。如可以表示为"P]K=25Pa"， 不可以表示为"P=25Pa （水)"; 质量分数为10%，不能表示为10% (m/m) 或10 % (by weight)。
4、单位名称与单位符号的使用界限。在自然科学论文，无论是叙述时还是公式图表中，应全部使用单位符号，而不能使用单位的中文名称。在社会科学论文中，在叙述中也要优先使用单位符号，运算和图表中只能使用符号。
5、在相除构成的组合单位符号中，不能多于一条斜线。如果多于一条， 多余的斜线下的单位表示负幂次，如J/kg/K应表示为如（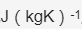
）
6、词头符号与单位符号构成倍数和分数单位时，按一个单位处理，中间不加字符，不分开。单位名称的读音也不能分开，最典型的是“摄氏度”，如20°C读为“20摄氏度”而不是"摄氏20度"。
7、与计算机相关的一些单位符号，应特别注意规范表达。如带宽4M，属单独使用词头; bps应为bytes/s; Kbytes中的K不是SI词头中的k，前者是1024倍，后者是1000倍。
8、只有我国的法定计量单位规定或认可的单位，方可用于表示量值的大小。为方便某些特定读者群，一些个别的非法定计量单位可在括号中表示或解释，如"动脉血压16 kPa (120 mmHg) "，这在涉及大众生活的论文中可以出现。
9、应避免不规范的单位缩写，例如，不可用sec代替s或second,不能用cc代替cm3或cubic centimeter, 避免用mps代替m. s-1或meterper second, rpm应改为r.min-1, 等等.
10、相对分子质量(Mr)不需要单位。
11、单位与文字信息不能混合使用，如the water content is 20mL :kg-1不能表述为20 mL H2O/kg或20 mL of water/kg。
12、单位符号与单位名称不能混淆，如“米每秒”、 “立方米”是单位名称，相应的单位符号则是m/s、m3或米秒、 米3，单位名称不能代替单位用于表示量值。
读单位也要讲效率。一般的原则是按书写顺序读,乘的符号不读，除的符号读为"每"， 方次的名称读在单位之前，单位和词头符号读其名称，不能按字母读音，物理量可以读名称，也可以读字母。注意平方与二次方的区别，只有在表示面积时，幂指数2可读为平方。立方与三次方也是这样，除表示体积时可读为“立方”外，其他地方幂指数3-律读为三次方。
在量和单位的表示中，有几个要求:
1、所有的单位符号必须使用正体。对于单位的词头符号，当所表示的因数小于106时用小写，其余则用大写;对其他单位的外文符号，凡是由人名演化来的，符号的第一个字母要大写， 其余-概小写;相除构成的组合单位，分子分母要写在同一水平线上(在运算过程中可以表示成分数形式)。
2、所有的物理量的符号必须用斜体表示。所有的非物理量、常数、标准函数等，统统使用正体，如圆周率(?) 、自然对数的底(e)、三角函数与反三角函数(sin、 cos、 tan、 cot..) 、双曲函数(sh、 ch、th)、对数(log、 In)、实部和虚部(Re、Im)、复数(i)等。
需要注意的是，在论文中经常有自己定义量的符号的情况，如果用单字母，应为斜体，如果用多字母或英语单词，为了美观应用正体。
3、所有表示顺序的字母不是量的符号，应表示为正体，如图2a、茅于轼(2012b)等。
在论文中，单位的中文符号与外文符号具有同等效力，但全文体例必须统一。
在实际应用中，常见的计量单位错误参见表2。
注: a——不符合国标规定; b——不符合国际规定; C——不符合书写规则;d——作符号时用简称。
