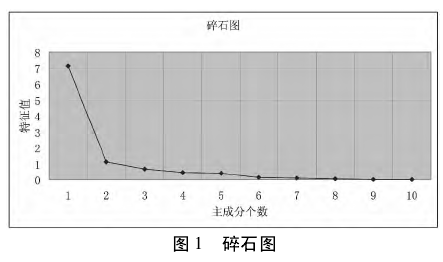
根据特征值的累计百分率超过方差贡献的百分数 85%,选择 4 个主成分,碎石图见图 1.
主成分表达式如下:
F1= 0. 305043* x1+ 0. 2265202* x2- 0. 268039* x3+ 0. 3517024* x4+ 0. 1429947* x5- 0. 362127* x6+ 0. 3583347 * x7- 0. 347691 * x8- 0. 358158* x9- 0. 361862* x10.
F2=0. 07635514* x1-0. 5772297* x2+0. 3285513* x3- 0. 0629 * x4+ 0. 71925865 * x5+ 0. 026 * x6+ 0. 0676 * x7- 0. 1019076 * x8- 0. 0927 * x9-0. 0867* x10.
F3= - 0. 388538349* x1+ 0. 477823835* x2-0. 239022143* x3+ 0. 232796412* x4+ 0. 630848574* x5+ 0. 0338 * x6- 0. 0367 * x7+ 0. 23 * x8+0. 169848928* x9+ 0. 164884252* x10.
F4= - 0. 1071797* x1+ 0. 43838322* x2+0. 86026821* x3+ 0. 14854684* x4- 0. 0453* x5-0. 0951 * x6- 0. 000344 * x7- 0. 1290782 * x8-0. 0661* x9- 0. 0455* x10.
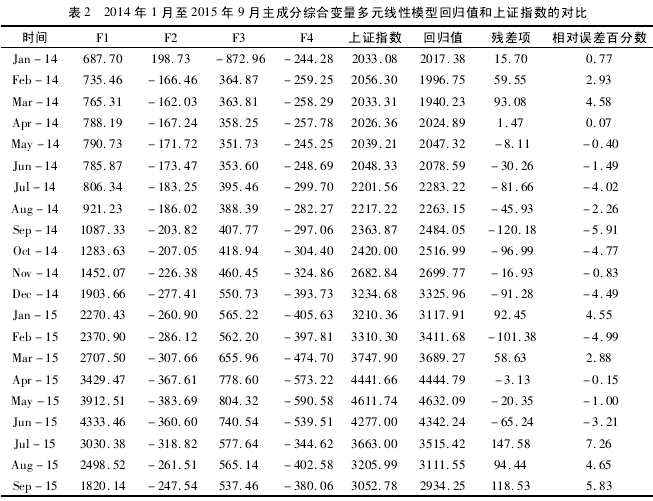
本文根据上述四个主成分生成自变量和因变量数据表格( 表二) ,并据此数据重建多元回归线性模型。从多元线性模型的四个综合成分自变量的回归系数显着性检验的结果来看,t 分布临界值为 t0. 025( 16) = 2. 119,而 F1 自变量的 t 检验值为2. 098 不能通过回归系数检验,其余主成分满足显着性 t 检验。
1. 2. 3 建立符合要求的多元回归线性模型。
将主成分变量 F1 剔除,构建以 F2,F3 和 F4为自变量的回归模型,方程式如下:
Y = 49. 5958 - 12. 6504 * F2 - 3. 8138 * F3 -4. 7181* F4.回归系数通过 t0. 025( 17) = 2. 101 的检验,表明主成分变量 F2,F3 和 F4 显着。其偏相关系数分别为 -0. 9268,-0. 9221 和 -0. 9541,表明上证指数对 F2,F3 和 F4 的依赖程度均高,且对F4 的依赖度略高一些。回归方程的 F 统计量为665,大于 F( 3,17) = 3. 20( 5% 的显着水平) ,说明回归方程的回归拟合效果显着。模型的复相关系数 R2 为 0. 9916,说明方程的拟合度很高。模型计算结果和实际上证指数的对比结果见表 2.
从上表回归模型和实际上证指数误差数据可以看出,建立在主成分分析基础上的上证指数多元线性回归关联式,消除了原始变量之间的多重共线性,无论是回归系数还是回归方程均为显着,复相关系数也表明方程的拟合度高,总体显着性好。2014 年 1 月至 2015 年 9 月的模型回归值与上证指数实际值的误差除了 2015 年 7 月以外,均在 6%之下,可以作为上证指数变化的参考依据,用以作为股票投资的基本判断。
因为回归模型不能及时体现离散事件的短期影响,当期相对误差会明显加大。以 2015 年 7 月为例,当期遭遇了 A 股上市公司大面积停牌,至月8 日收盘,两市共1312 只股票停盘,占 A 股市场的 47. 2%.同时,监管层救市政策出台,中央汇金入市操作等事件的合力冲击造成 7 月的模型回归值相对误差达到 7. 26%.故在借鉴回归模型的参考指导外,还需高度关注政策( 如本次的降杠杆,去除场外配资的政策) 引发的冲击事件对股市造成的影响。
2 总结。
股票作为一个金融产品,其影响因素是多方面的。本文通过对股市上呈现的数据进行挖掘,利用统计方法从宏观经济指标方面分析了对上证指数的影响。在常见宏观经济指标中,选取了对上证指数有明显影响作用的指标,通过主成分分析消除了各原始因素之间的多重共线性,建立了以主成分综合变量为自变量,上证指数为因变量的多元线性回归关联式。借助于上述所得的模型和结论,可以为个人在规避市场系统风险提供一个参考依据,从而降低市场系统性风险对个人股票投资带来的损失及提高本金收益率。
参考文献:
[1] 傅德印 . Excel 与多元统计分析 - 附实用计算机程序[M]. 北京: 中国统计出版社,2007.
[2] 左 媛 . 上市公司盈利质量分析[J]. 安徽冶金科技职业学院学报,2012,1 .