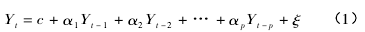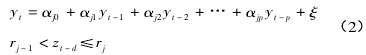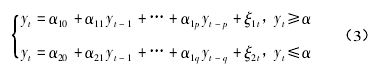三、理论分析。
在金融时间序列分析中,对于平稳的时间序列人们通常建立 AR 模型拟合其非线性演变特征[11].通常情况下如果一个时间序列满足:
则称时间序列{ yt} ,t =1,2,…为 AR( P) 过程。随着我国市场经济的不断完善、改革开放进程的不断深入以及计算机和互联网技术的空前发展,我国股票市场也发生了重大变化,各种金融衍生品层出不穷、金融市场规模和金融交易频率空前扩张导致金融时间序列往往呈现结构性突变或跳跃现象。因此,为了拟合当前金融时间序列的非线性特征,学者们提出了 TAR 模型。一般情况下,如果时间序列{ yt} ,t =1,2,…满足:
则称为一个 k 段门限自回归模型。其中 zt - d为门限变量,是可测的。rj为门限值,k 为正整数,是TAR 模型的段数,ξ 为服从独立同分布的随机白噪声序列。在实际研究过程中,人们经常采用 Tong和 Lim 提出的 TAR 模型[18],其一般形式可以表示为:
其中,α 为阈值,是未知量,本文通过 Chan 提出的网格搜索法进行确定[19].同时 TAR 模型也表明在金融时间序列中通过阈值将其分为若干部分,考虑到了金融时间序列的结构性突变或跳跃现象。
四、实证分析。
( 一) 基于 Johansen 协整检验方法的股价泡沫分离。
股票价格受到宏观经济形势相关变量影响有国民经济总体指标、投资指标、消费指标和金融指标[20].国民经济总体指标一般用国内生产总值和工业增加值等衡量,投资指标一般用全社会固定资产投资额衡量,消费指标指社会消费品零售总额和城乡居民储蓄存款余额,金融指标一般用货币供应量、利率和汇率等衡量。为了直接反映银行体系对股市泡沫的影响,本文采用各项贷款指标。鉴于统计局网站没有公开工业增加值数据,本文选取制造业采购经理指数作为替代,选取广义货币与狭义货币之差( M2M1) 、金融机构各项贷款总量( Loan) 、消费者价格指数( CPI) 、汇率( FE)和制造业采购经理指数( PMI) 5 个宏观经济变量作为解释变量,上证指数月度收盘均价( ShanghaiComposite Index Monthly Closing Price,简称 SCIM-CP) 作为被解释变量。所选数据的时间窗口为2006 年 1 月到 2015 年 5 月。
在协整检验之前,为消除季节变动等因素的影响,本文对上证指数收盘均价、消费者价格指数、汇率、广狭义货币差和各项贷款做对数变换,并且对制造业采购经理指数等 6 个经济变量时间序列做 X-11 平滑处理并做协整回归,得出协整方程和协整残差即股价泡沫。对股价泡沫进行平稳性检验和自相关检验,如果股价泡沫序列没有通过两个检验的任何一个就说明协整残差中存在股价泡沫。对股价泡沫建立 AR 和 TAR 模型,辨别模型的拟合效果。如果 AR 模型拟合效果优于TAR 模型则说明上证指数股价泡沫不存在结构断点或突变特征。根据协整回归结果以及 AR 和TAR 模型的拟合股价泡沫的优劣差别得出结论并提出建议。
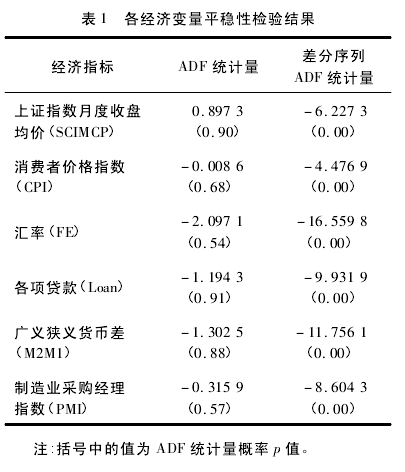
协整理论要求每个时间序列是非平稳的,因此本文对 6 个时间序列进行平稳性检验,结果如表 1 所示。
通过对各经济变量进行平稳性检验得出各经济变量原序列都无法拒绝存在单位根的原假设,汇率的二阶差分序列以及其他 5 个变量的一阶差分序列在 1%水平拒绝了存在单位根的假设,即汇率为 I( 2) 过程,其他 5 个变量序列均为 I( 1) 过程。为剔除股票价格的实际价格,本文对 6 个经济变量进行 Johansen 协整检验,结果如表 2 所示。