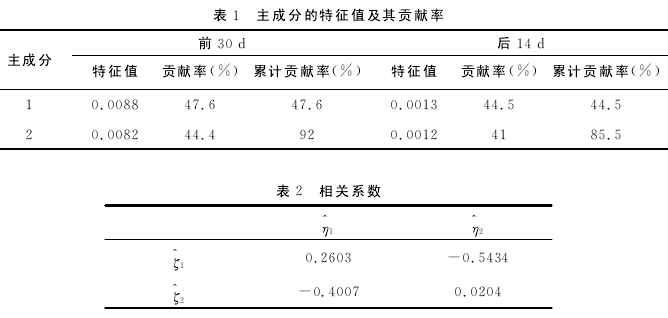
根据表1中的方差贡献率,在第一区间选取前2个主成分,在第二个区间里,选取前2个主成分。
根据上表的相关系数,使用最小二乘估计,可以得到如下的非线性模型,从而得到PCP(q;p1,p2,…,pq)模型为:
其中
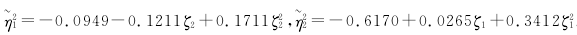
。
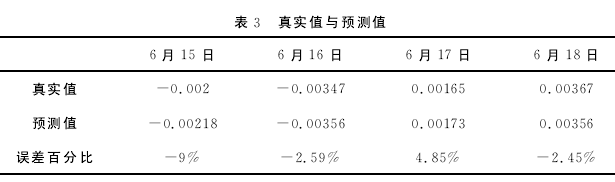
观测到的真实值、模型估计出的预测值及由两者得到的误差百分比如下表所示。
由表3可以看出,除6月15日误差百分比较大以外,绝大部分的误差百分比都较小。即建立的PCP(2;2)模型的准确性较高。综上知,使用函数型主成分预测模型预测上证指数收益率的准确程度较高。
3结论。
本文给出了函数型数据分析方法在上证指数中的应用,研究了函数型数据的主成分分析方法以及如何建立函数型主成分预测模型。通过对上证指数收益率进行预测的实证分析,可以看出建立函数型主成分预测模型对我国上证指数收益率进行预测,预测的准确程度较高。
参考文献:
[1]Ramsay J O.When the data are functions[J].Psychometrika,1982(47):379-396.
[2]Ramsay J O,Hooker G.Functional Data Analysis with R and MATLAB[M].New York:Springer,2009.
[3]Shang H.L.Nonparametric modeling and forecasting electricity demand:an empirical study[J].2010(Working Paper)。
[4]Mallor F,Leon T,Gaston M.Changes in power curve shapes as an indicator of fatigue during dynam-ic contractions[J].Journal of Biomechanics,2010(43):1627-1631.
[5]Delicado.P.Dimensionality reduction when data are density functions[J].Computational Statisticsand Data Analysis.2011:401-420.
[6]Berrendero J.R.Principal components for multivariate functional data[J].Computational Statisticsand Data Analysis.2011:2619-2634.
[7]严明义。季节数据分析:一种基于数据的函数性视角的分析方法。当代经济科学[J].2007(1):108-113.
[8]严明义,等。中国消费价格指数季节被动的函数性数据分析[J].统计于信息论坛,2010(8):100-106.
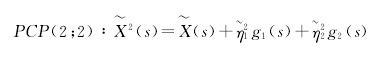
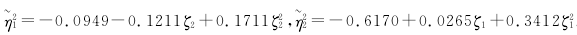 。
。