第三章美国洪水保险需求非理性行为分析
第一节美国洪水保险项目(NFIP)介绍
美国是洪水灾害频繁发生并经常导致其巨额损失的国家,洪水灾害影响人口约三千万,深深地威胁着美国百分之七的国土。在美国,有较大洪水风险的城镇达五千多个。自十九世纪末,美国就认识到洪水灾害的严重性,并开始大量建设防洪工程,但在之后的几十年,这些都没有改变水灾造成的损失以及政府救济支出的增长趋势,而且建设防洪工程和政府救灾这两项支出都非常高昂,于是美国政府希望能够通过建立洪水灾害保险制度来降低财政负担。但私人保险公司认为洪水灾害风险是不可保风险,一般设为保单的除外责任,所以在1956年,美国国会通过了《联邦洪水保险法》,确定了联邦洪水保险制度。但方案最后却因为美国国会没有拨款而搁浅。之后发生的一次严重灾害强烈要求美国建立水灾保险制度,这促使1968年美国国会通过《全国洪水保险法》并在第二年开办国家洪水保险项目(NFIP),成立了国家洪水保险基金。至此,美国联邦政府正式建立起国家洪水保险制度并在之后几十年间的不断完善。
一、美国洪水保险运营模式
美国洪水保险项目(NFIP)由政府主导,为了对该项目进行管理,美国联邦政府成立了经营和管理洪水保险专门机构一联邦保险管理局(FIA)。FIA在1979年后由联邦紧急事务管理署(FEMA)领导。联邦应急管理署隶属国土安全部,总部设在华盛顿,在全国各地建有办事处,4000人随时待命应对灾害。联邦应急管理署的中心任务是保护国家免受各种灾害,减少财产和人员损失。这种灾害不仅包括飓风、地震、洪水、火灾等自然灾害,还包括恐怖袭击和其他人为灾难。
最终形成一个建立在风险基础上的综合性应急管理系统,涵盖灾害预防、保护、反应、恢复和减灾各个领域。由于NFIP是政府管理的,所以美国的私人保险公司只是负责代理收取保费并获取佣金,而不直接参与洪水保险的用作,当然也不承担任何保险风险。美国政府和保险公司签订WYOi计划以利用商业保险公司的营业网点达到销售洪水保险的目的。保险公司收取的保费要讲给FIA统一管理。
一旦洪水灾害发生,由保险公司办理相关赔付手续并垫付赔偿金,之后再由联邦政府赔偿。NFIP由政府全部承担洪水灾害的风险和损失,并没有再设立再保险公司以分散风险。而NFIP的洪水保险赔偿资金和运营资金通过保险金支持,并享受免税待遇。当洪水灾害造成的损失巨大,保险基金无法全部赔偿时,就可以由国家拨款,以后再由保险金偿还。因此,政府在美国的洪水保险制度中充当的角色是保险人和最后保险人。另外值得一提的事,美国的资本市场较为发达,利用这一点,美国设计出一些巨灾衍生工具包括巨灾债券、巨灾期货和巨灾期权等来转移巨灾风险。
二、美国洪水保险产品特点
美国洪水保险项目(NFIP)的保险范围包括由于山洪爆发、江河泛滥等对建筑物及建筑内部财产所造成的冲毁、浸泡、淹没等造成的损失。NFIP的承保从社区开始,每个社区想要参加NFIP必须采取一定的防灾减灾措施,而想购买洪水保险的个人其所在社区必须是NFIP成员。美国洪水保险项目并不具有严格的强制性,除了要求洪水高危区的社区必须参加NFIP之外,联邦政府主要是采取一些其他措施激励社区加入该项目。比如,没有参加该项目的社区洪水灾害发生后不仅无法享受政府的灾害救济,在其他一些政府机构的项目上也无法享受优待。另外,NFIP分别承保家庭财产和企业财产,企业财产中也只承保一些对家庭生活相关的小企业,而不承保大型企业。对于家庭和企业,NFIP收取的费率也不相同,企业费率按实际征收,而家庭保险的费率则会接受财政补贴。FEMA根据不同地区面临的不同洪水风险来统一制定保险费率图。保险费率图将美国各地区划分为不同的风险区,并且会随着各地区实际环境和防灾减灾工程的改变而进行修改。NFIP设定最高承保限额并对限额内的损失全额赔偿,而超过部分投保人可以选择投保其他商业财险。
第二节居民对洪水保险需求的模型分析
在了解了美国洪水保险制度之后,我们将以此为例用模型的方法分析居民在.
购买洪水保险时的非理性行为,以印证我们之前从行为经济学角度的分析。本节将构建一个简单的期望效用模型来分析美国居民购买洪水保险的行为,然后再用修正的贝叶斯模型分析居民对洪水发生概率的学习过程。
一、居民的期望效用模型
在美国洪水保险项目中,居民按年购买保险,每年按照其对洪水灾害发生的概率的预期选择自身购买的保险额度以最大化他的期望效用。对于居民i来说,他的期望效用模型如下

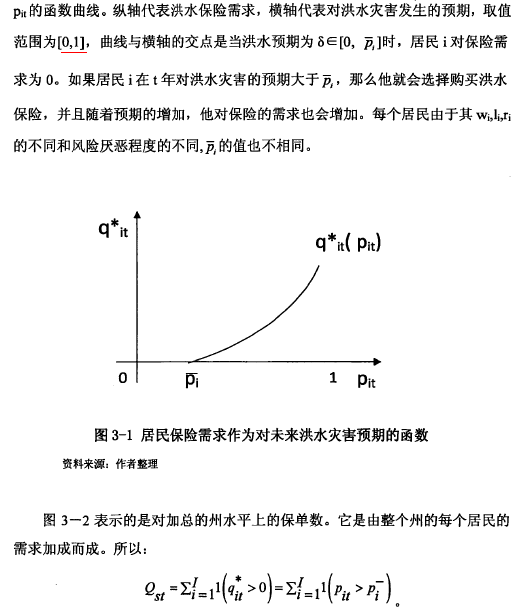
因此州保单需求量也与居民对洪水发生的预期相关。图3—2中,表示了三个居民不同的需求曲线,我们假设同一个州的居民具有相同学习曲线,也就是说他们根据同样的消息调整自己对洪灾发生概率的预期值,因而得到相同的预期Pt,但是我们可以看出在pit=P2t=P3t的位置,对于居民1和2将会选择购买保险,而居民3却不会购买。这是因为各居民虽然预期一致,但因受w,U等影响的需求曲线却各不相同,做出的购买决策也不相同。
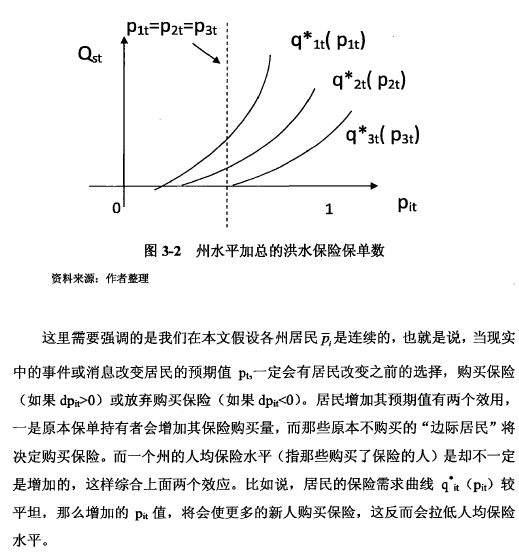
如果我们放开各州每个居民具有相同洪水灾害预期的假设,我们的分析可以同上述相似,只不过每个人根据其所在地区和是否有洪水灾害发生来更新他的预期值,但在影响居民购买行为上是一致的。
二、居民Beta-BeraouUi Bayesian学习模型及其修正
在上一小节中,我们讲到居民通过选择购买保险的行为最大化自身的期望效应,而保险购买水平则与居民对洪水灾害发生概率的预期值成正相关关系。每年居民根据发生的洪水灾害来更新自己的预期。这一节,我们将构建居民学习模型来分析其形成自己的预期的过程。

近些年已经有很多实证经济研究支持贝叶斯学习理论。其中与本文研究方法较相似的是Davis (2004),Davis将居、民对特定癌症风险的学习过程建立模型并假设居民将某个服从伯努利分布的特走癌症风险中提取未知的参数。二十一世纪前几年,在纳华达州一个人烟稀少的丘吉尔县,出现大量被诊断为白血病的案例,这个“癌症集群”被当地和全国的媒体广泛宣传。Davis指出随着该县白血病病例的增加,同期房地产的价值在下降。这个证据与Beta-Bemoulli Bayesian学习模型是一致的,因为人们根据白血病案例的出现来调整自己对白血病风险的预期值并反映在他们对购买房屋愿意支付的价格上。
Bayesian学习模型在其他一些情景中却与实际数据并不相符,这包括一些对金融市场的投资决策和过去股市收益的实证研究(Ulrike and Nagel, 2010)。所有投资者都可以获得同样股票收益的历史数据,但是作者发现,个人投资者更更可能对那些低回报的股市投资有个人经验。
另外一些学习模型被创建来解释观察到的行为模式,这些理论中许多能够在心理学中找到根源。信念学习理论强调第一手经验在解释信息的重要性,选择“强化”模型认为人们的策略行为被他们以前的支付强化,倾向与选择那些受强化的策略。选择强化模型主要强调两种偏离Beta-Bemoulli Bayesian学习模型的理论。
第一个差异就是接受完全相同信息的个体会基于他们之前的经验而形成不一样的对未来的预期,第二个差异是个体会折旧他过去的信息。如果潜在的分布是稳定的(例如本文研究的洪水灾害),那么折旧过去的信息将会与Beta-BemoulliBayesian学习模型不一致。对于当洪水灾害分布稳定,而个体会折旧过去的信息的一种解释是个体的“健忘性”。







