第四章居民非理性行为对美国洪水保险需求影响的实证分析
本章我们将用实证分析的方法证明居民的非理性行为是如何影响美国洪水保险需求的。我们釆用的面板数据模型进行实证分析,统计计量软件使用的是statall.O。
第一节样本的选取
美国的洪水保险制度由政府主导已发展成熟,成立美国洪水保险项目(NFIP)管理并由联邦应急管理署(FEMA)统一管理。FEMA根据美国各地区面临的洪水灾害风险不同,对各地区分别制定不同的费率,并且NFIP保单有效期为一年。因此,在样本选取上,我们选择的是美国50个州加上哥伦比亚特if各年度的数据,另外因为我们只能获取1996年-2013年各州洪水保险保单的数据,所以保单数据的时间长度为18年,洪水灾害的数据为1987年-2013年。样本数据的来源为:洪水保险保单量来自于美国联邦应急管理署(FEMA)、洪水灾害带来的损失来自于美国联邦应急管理署(FEMA)和保险信息协会(111)。美国人口的数据来源于全球经济数据库(CEIC)。
第二节变量的选取
在变量选取上,我们要结合前面两章的分析,第二章我们分析了可得性偏差和显着性偏差使得投保人总是给予最近的信息比较大的权重,而常常忽略较早的信息,这使得个人对风险的判断往往比较主观。在巨灾事故发生后,周围环境的变化以及媒体的报道使得投保人的感官受到刺激,使其过分重视事故造成的伤害和损失,导致其因灾害的发生产生紧张或恐惧的情绪,并产生对巨灾事件产生非理性的判断,从而忽视了巨灾事件小概率的特点,增加对巨灾保险的需求。而随着巨灾发生的时间过去,人们就逐渐淡化记忆,投保人的也会逐渐转移其注意力,逐渐恢复其对巨灾事故小概率特点的认知。这时候,投保人会选择不再购买或者减少购买巨灾保险。
而第三章我们用居民期望效用模型和居民学习模型对美国洪水保险的需求进行了理论分析,居民对洪水保险需求与其对洪水灾害发生的预期成正相关关系,如果洪水灾害发生,那么居民就会增加他的预期值,我们假设对于各州的居民来说,是连续的,那么居民增加其预期值有两个效用,一是原本保单持有者会增加其保险购买量,而那些原本不购买的“边际居民”将决定购买保险。
因此,为了反映非理性因素对美国居民对洪水保险需求的影响,我们选择被解释变量为人均保单数,保单数和保费收入同样能反映对洪水保险的需求,这里选择人均保单数是因为这更能形象地反映出当人们增加对洪水灾害发生概率的预期时,那些处于“边际”地位的居民开始购买洪水保险。而解释变量本文选取的是洪水灾害造成的经济损失。选取洪水灾害损失作为解释变量的原因在于,之前我们分析居民会在发生灾害时更新之前的洪水灾害预期,而洪水造成的损失越多,我们可以认为被洪水影响的人群越大,那么就有越多的人改变之前的预期,就会有更多的人选择购买洪水保险。因此,我们的预期是,洪水灾害造成的损失会对洪水保险需求有显着的影响,并且会持续影响一段时间。另外,根据人们的“健忘性”,人们会折旧过去洪水灾害的信息,所以越是近期的洪水灾害影响需求的权重越大,而较早期的洪水灾害对居民的购买行为影响减弱甚至消失。
洪水灾害损失的数据来自与联邦应急管理署的Presidential DisasterDeclaration (PDD)体系,该体系的建立是为了灾害发生后能够及时的披露信息和获取援助。并非所有的洪水灾害都能够进入这个体系,各地区灾情发生后要想联邦应急管理署申请,联邦应急管理署不会接受所有的申请,而是根据灾情的损失程度以及其他一些考虑来决定是否接受申请。历史数据统计,联邦应急管理接受了大约三分之二的申请。因此,在我们的样本中洪水灾害损失的数据是除去了联邦应急管理署拒绝那些损失数据,但由于那些数据占比较小,并且大多洪水灾害造成的损失和影响范围也小,所以不影响我们的实证分析。
第三节模型的建立
接下来我们建立回归模型。根据我们对变量的选取,我们建立如下回归模型:
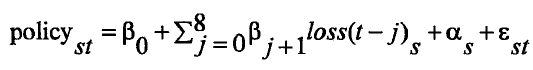
loss代表各期各州洪水灾害带来的损失,因为影响洪水保险需求的不止当期发生的灾害,还包括以前发生的洪水灾害,因此这里我们将洪灾损失这个解释变量滞后了九期,来考察之前年份洪水灾害损失对特定年份保险需求的解释力度。P。是常数项,S,,是随机扰动项,(X,是各州的固定效应,这里我们将回归模型设定为固定效应模型,是因为对于洪水风险来说,地区的不同导致其面临风险程度不同,FEMA对其征收的保费也不同,因此必然存在个体效应,另外我们只需要考虑洪水灾害损失对洪水保险需求的影响,我们可以将其他因素设定为与各州相关的个体效应。关于固定效应模型的选择我们会在后面再做相关检验。
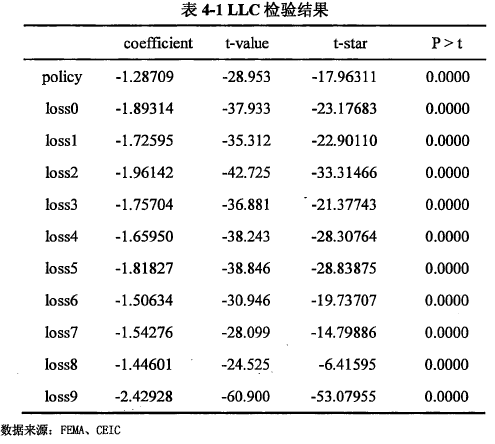
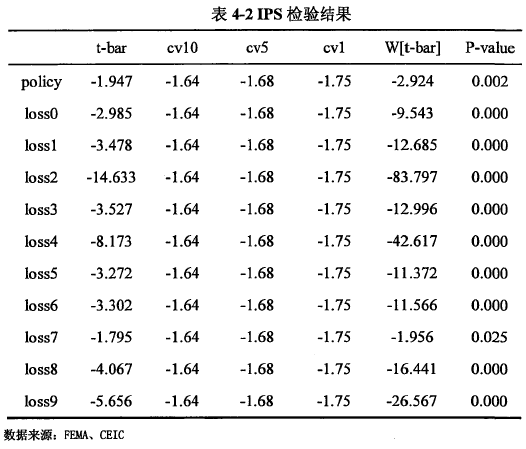
由于我们对面板数据进行回归,我们首先来进行单位根检验以确认数据的平稳性,这里选择的检验方法,选择的是不同跟和同根的检验各一种:LLC和IPS检验。LLC检验结果如表4-1所示,IPS检验结果如表4-2所示,两种检验都表明所有变量拒绝原假设,通过平稳性检验。
因为我们使用的是面板数据,这时一般有三种不同的估计模型,分别是混合回归、随机效应模型和固定效应模型。混合回归模型将面板数据完全看成横截面数据,是一种极端的估计方法,忽略了个体之间的异质性,要求样本中的个体有相同的回归方程,混合回归一般是有偏的。固定效应和随机效应模型则考虑个体的异质性,只要求个体有相同的斜率,可以有不同的截距项。如果代表个体异质性的截距项与模型中某个解释变量相关,则应使用固定效应模型,否则应使用随机效应模型。虽然前面我们已经分析最适合本文的回归模型是固定效应模型,因为各州的个体效应必然存在,但我们还是需要用检验的方式确定使用哪种模型。
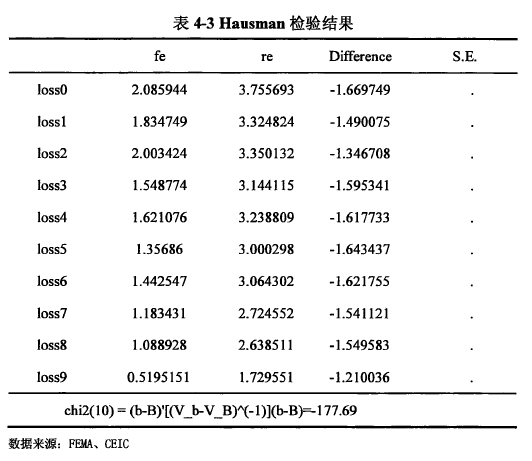
首先判断是用混合回归模型还是固定效应模型应使用F检验。Statall.O的输出结果报告的F检验值及其P值为F(50,857) = 2222.05, Prob> F = 0.0000,因此我们拒绝原假设,再做进一步的检验。第二步我们判断应当使用随机效用模型还是固定效应模型,这种情况下个的检验方法是Hausman.检验。
Hauman检验的原假设为代表个体异质性的截距项与解释变量均不相关。如果接受H。,则应当使用随机效应模型,如果拒绝He,则应使用固定效应模型。图4-1是Hausman检验的结果。我们可以看出检验结果中出现卡方值为负的现象,这种情况一般来说是因为我们在模拟两种模型时主要是RE模型的基本假设Corr(x_it, u_i) =0无法得到满足,这种情况下我们一般选择拒绝随机效应,而选择固定效应模型。
第四节实证结果
在我们的模型通过检验之后,我们就可以进行回归了。回归的结果如表4-2所示。
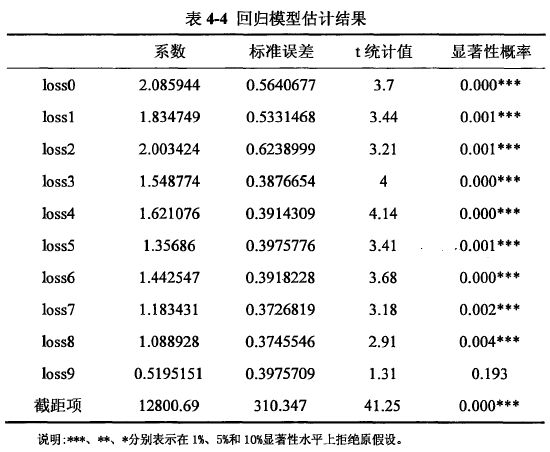
我们从估计结果可以看到,从当期的损失lossO开始到滞后8期的损失loSS8对保险的购买量都显着影响,滞后九期的损失loss9不再显着。另外我们还可以观察出各期损失值影响系数大致呈递减趋势,这正符合我们之前对结果的预计,当期的洪水灾害损失对居民洪水保险需求的影响最大,而滞后期数越久,影响就越小,这是因为人们具有“健忘性”,对以前的信息折旧。到loss9就基本不会显着影响洪水保险的购买了。而各期影响系数的减少程度是由我们的“折旧率” S影响的。
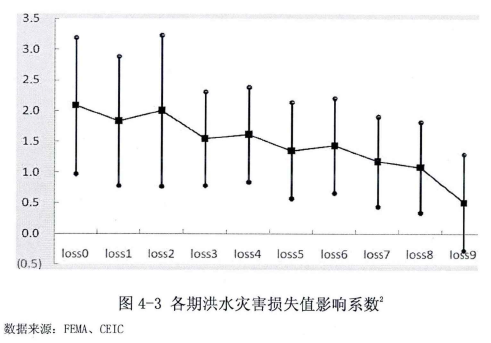
图4-3是根据回归系数在95%置信区间的值的绘图,横轴是代表各期损失,纵轴代表系数值。我们可以明显地看出影响系数递减的趋势。





