第四章 基于专业服务的高等数学在高职各专业的应用举例
数学建模就是应用数学知识、数学的方法论,认识现象、理解现象、用数学描述现象并解释现象的过程,它是对现实问题为了某种目的而作出抽象、简单的一种数学结构。将数学建模的思想与方法引入到高职高等数学课堂,能够充分展示数学的应用价值,彰显高等数学的特色,可以使数学教学实现由“实践——理论——再实践”的过程,促进高职数学教学与专业实际问题的解决联系起来,达到学以致用的目的,保证高等数学的教学模式与高职院校“工学结合”的人才培养模式相吻合。
在高职数学教学中融入数学建模活动、积极尝试案例教学,可以打破原有数学课程的架构与内容体系,创新高职数学教学模式,建立高等数学与专业课程及实际问题的广泛联系,让学生亲自发现专业与数学知识的对接点,扩大数学在专业或专业群中的应用,激发学生的学习热情,培养学生的创新精神。
数学建模问题多种多样,建模思路、方法、过程及使用的数学工具不尽相同,发展空间十分广阔,建模活动不追求知识和结果,关注过程的合理和技能的提升,数学建模要经过哪些具体步骤并没有统一的模式,但人们总结出了数学建模的一般过程,具有普遍的指导意义。其一般步骤为:

4.1.1 银行借贷问题
4.1.1.1 问题的提出
随着人们生活水平的提高,同时也随着房价的不断上升,人们开始向银行申请个人住房贷款。其还款方式有以下两种:
(1)等本不等息递减还款法。即每月还贷本金相同,利息逐月减少。
(2)等额本息还款法。即每月以相等的额度平均偿还贷款本息。
请分析这两种还贷方式的利弊。
4.1.1.2 问题的解决
设贷款 20 万元,分 30 年还清,年利率 5.04%(即月利率 0.42%)。
(1)第一种还款方式




第一种还款方式(等额本金)是前期还款压力比较大,后期还款压力较小,这种还款方式最省利息。第二种还款方式(等额本息)是每月的还款额相等,还款压力相对较小,但是贷款产生的利息较多。
4.1.2 保险收益问题
4.1.2.1 问题的提出
中国人寿保险公司推出了新生儿保险业务,保险合同中的有关条款为:投保范围是未满一周岁的新生儿,投保人需连续缴纳保险费,且每年交费 1694 元,保险公司的给付金额情况是:被保险人 18 岁时,给付成人保险金 1 万元;被保险人 22 岁时,给付创业保险金 1 万元;被保险人 25 岁时,给付婚嫁保险金 1 万元。
现在,如果不考虑保险的其他功能,仅从储蓄的角度出发分析探讨问题。
(1)假如银行年连续复利率 r=0.02,比较买保险和直接存款那种方式更合算;
(2)假如银行年连续复利率 r=0.02, 且给付婚嫁保险金 1.5 万元,比较买保险和直接存款那种方式合算;
(3)假如银行年连续复利率 r=0.05, 且给付婚嫁保险金 1.5 万元,比较买保险和直接存款那种方式合算。
4.1.2.2 问题的解决
为了对保险和直接存款能在同一层面上进行比较,我们通常就投保人缴纳的保险费和保险公司给付的保险金额分别进行现值计算,然后就现值进行比较,从而得出本题的结论。
(1)投保人缴纳保险费的现值计算——收益现值法

4.2 基于专业服务的高等数学在农林类专业的应用
4.2.1 饲料配比问题
4.2.1.1 问题的提出
在高职畜牧兽医类专业,动物的饲料配比问题,是一个十分重要的现实课题,如何做好饲料配比分析,是高职数学课程在专业应用上的具体表现。例如:某种动物的生长对饲料中蛋白质、矿物质、维生素的含量有明确要求,每个动物每天至少需要蛋白质70g、矿物质 3g、维生素 10mg,公司从市场中购买了 5 种不同的饲料,每千克饲料中的营养成分含量如表 5-1,5 种饲料每千克的成本如表 5-2。为了满足动物营养需要,如何制定饲料配比,能使公司购买饲料的成本最少?
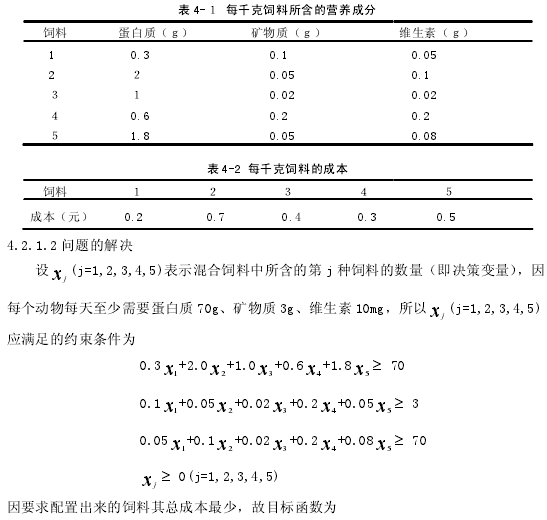


4.2.2 技术方案综合评价问题
4.2.2.1 问题的提出
现有 5 个农业技术经济方案,如表 5-3 所示,是评价各方案的优劣。

通过相对偏差矩阵 R 的构造,不仅消除了量纲,使各项指标具有可比性;同时由于在理性方案的基础上构建,使之实现了一种最优。
(3)确定指标权重
综合评价是通过多种指标来进行的,指标通常有一个权重的问题。权重的设定方法有很多,这里我们根据权重的设定理论:“如果某种指标的数值能明确区分开各个被评价的对象,说明该指标在这项评价上的分辨信息丰富,因而应给该项指标以较大的权重;反之,认为权重较小”来设定指标权重。其中的区分度利用方差来体现,具体表述如下:




4.3 基于专业服务的高等数学在其它专业的应用
4.3.1 城市垃圾处理问题
4.3.1.1 问题的提出
根据某城市 2010 年年初所做的统计资料显示,到 2009 年年末,该城市堆积的垃圾已达 50 万吨,侵占了大量的土地,并且成为造成环境污染的重要因素之一。根据统计和预测,从 2009 年起该城市还将以每年 3 万吨的速度产生新的垃圾,垃圾的资源化和回收已经成为城市建设中的重要问题。如果从 2010 年起,该城市每年处理上一年堆积垃圾的 20%,试问:
(1)10 年后,该城市垃圾是否能全部处理完成?


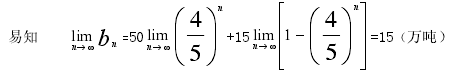
4.3.2 容器中盐水的含盐量问题
4.3.2.1 问题的提出
现有一很大的不规则容器,其中装有一定体积的盐水,从容器的一端向容器中注入一定浓度的盐水,混合后的盐水将从容器的另一端流出,试建立描述容器中盐水的浓度的动态变化过程。
这个问题看起来有较强的人为编撰的痕迹,但经过细心的认真分析,能够明白该问题确实是有其实际背景的,它是许多实际问题通过简化而得到的一种物理模型,因此,用数学模型来研究这个问题具有很强的实际意义。
4.3.2.2 问题的解决


从人类社会的历史发展来看:数学与日常生活及生产实际紧密相联,数学可以解决日常生活及大千世界中各种各样的实际问题。另外,科学的数学化、工程技术的数学化以及人文社会科学的数学化都已成为现实。随着现代职业教育体系的建立,数学在高职教育中的地位愈来愈重要,它已渗透并应用到高职的所有专业,可以说:数学的应用无处不在。除了上述所谈案例之外,还有其它专业的许多案例都可通过建立数学模型来解决。例如:机电类专业加工过程的最佳方案设计问题,石油化工专业的石油开采问题、新材料合成问题、节能问题、环境污染治理问题;建筑专业的建筑物的抗震问题;医学专业的糖尿病诊断问题、传染病问题;物流专业的最佳运输路径、最佳装载及最佳仓储问题等等。应该看到一切具体现象被数学化的过程就是进行数学建模,通过融数学建模于高职数学教学之中,可有效提高学生的应用能力和专业转型能力。
优秀的数学教学,不仅能使学生正确的认识和理解数学,而且还使学生学会了如何去掌握和运用数学。开展数学建模活动可以激发高职学生学好高等数学,只有学好高等数学才能为学生开展数学建模提供支持、创造条件。通过开展数学建模,不仅使学生思维得到锻炼、数学应用意识得到加强,而且使学生能积极主动地运用数学知识、分析解决行业、专业及日常生活中的实际问题数学建模的过程是一个创新的过程,数学建模不同于数学理论教学,其对实际问题的研究往往并不存在所谓的标准答案,随着对问题的深入理解,解决问题将是一个不断创新的过程。让学生去探讨一个非常实际的专业或行业问题,学生会产生浓厚的兴趣,其自主创新的能力将得到很好的发挥和培养。数学建模内容丰富、方法灵活、信息量大,不需要高深的数学理论和太严密的数学推导,非常适合高职学生的特点。因此,融数学建模于高职高等数学教学之中,积极开展案例式教学等数学实践活动,是高职高等数学教学为专业服务的重要举措。





