( 2) 实践过程: 先给出一个△ ABC ,为了方便教学,根据条件,引导学生以 A 为圆心,以 AB 、AC 为半径画的圆,可以得到△ AB'C'; 在这可以拖动圆上的点B‘和 C’点,可以让学生直观的感受,即使满足两边相等的条件作出的△ AB'C',也并不能使它和原△ ABC全等; 最后我们可以通过测量边的值来进一步验证出两个三角形的对应边并不能相等,所以判定两个三角形不能全等。
通过比较超级画板制作的课件与 PPT 制作的课件,可得出如下结论:
( 1) 检验所画的三角形与原来的三角形是否全等时,运用超级画板画的三角形在不用改变已知条件的情况下可以改变其形状,是“活的”,显现的是一种动态过程,其可以通过任意移动和精确测量来直观显现结论,因此,有助于提高学生的想象力和观察能力; 而PPT 展示的三角形是固定的,只能通过简单的动画显现没能重合,其难以直观形象地揭示三角形的本质特性。
( 2) 运用超级画板制作出来的课件可让学生操作体验,为下一步探索三角形三个边的关系培养类比、猜想和探索的能力; 而 PPT 缺乏交互性和可操作性。
案例 2: 《二次函数图象与性质》
利用 PPT 制作的教学课件:
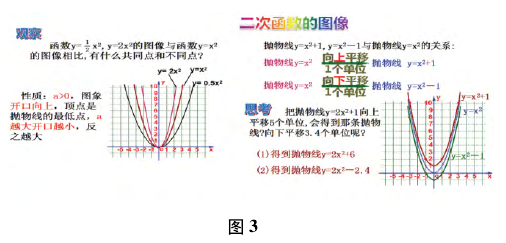
( 1) 思路分析: 探讨二次函数中 a,b,c 对函数图象的影响,这里采用分类讨论的方法,在坐标轴中,画出 a 与 c 值不同时的函数图象,可以通过观察得出结论( 图 3) .
( 2) 实践过程: 在同一个坐标轴中画出当 b,c 为 0,而 a 值不同时的图象,根据观察发现 a 的值决定的是函数图象的开口方向与开口大小; 在另一个坐标轴中画出当 a 值为定值,b 为 0 ,c 不同时的图象,观察得出 c 决定着函数图象与 y 轴 的交点,最后总结得出二次函数中 a,b,c 对函数图象的作用。
利用超级画板制作的教学课件:
( 1) 思路分析: 因为函数 y = ax2+ bx + c 的性质一直以来都是教学的一个难点,学生容易记忆混淆,因此,在这借助超级画板的动态演示,可以帮助学生理解并记忆。
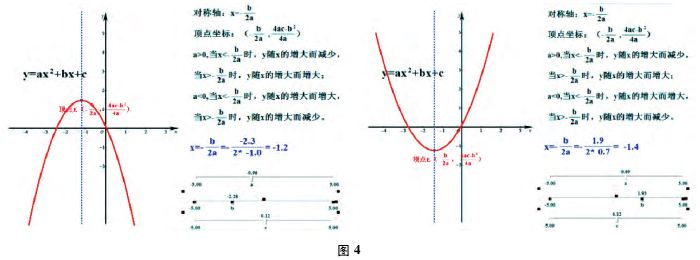
( 2) 实践过程: 如图 4 所示画出函数 y = ax2+ bx+ c 的图象,通过分别移项右下角的变量尺中的 a 、b 、c ,可以发现图象的变化规律,a 决定了函数的开口方向,c 决定与 y 轴的交点; 在这引发一个思考: b决定了函数的什么? 可以通过变量尺的移动,让学生直观的感受到 b 不能单独决定什么,但是它能与 a 共同决定函数的对称轴; 通过 a 为定值去移动 b ,以及测量对称轴的值,可以发现当 a 与 b 异号时,对称轴在 y 轴的右侧; 当 a 与 b 同号时,对称轴在 y 轴的左侧,从而得出函数 y = ax2+ bx + c 的性质。