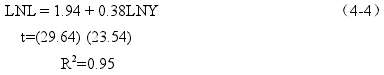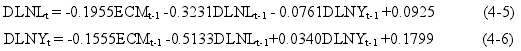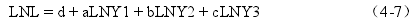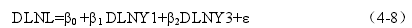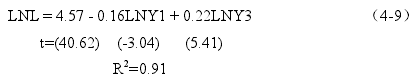西藏第三产业就业效应的回归分析

　　第四章 西藏第三产业就业效应的实证分析
　　
　　在了解西藏第三产业影响就业变化的事实基础上，运用计量分析法从实证角度探究西藏第三产业的就业效应，有助于从提高就业效应角度找出西藏第三产业未来发展方向。维持发展正就业效应大的行业，积极促进正就业效应小的行业，转变突破负就业效应行业。通过第三产业提高就业效应，解决西藏就业问题，有利于真正实现“稳藏”的国家战略决策。
　　
　　第一节 西藏第三产业就业效应的回归分析
　　
　　本章模型采用由柯布-道格拉斯函数 Y=AKɑLβ演变过来的回归模型
　　 　　
　　该回归模型表明产值 Y 对就业人数 L 具有一定的影响作用，其中 β 表示这种作用大小。本章利用计量分析软件 Eviews6.0 进行回归分析。
　　
　　付春光①（2011）认为分析我国第三产业促进就业的有效性既可以采用三次产业联动法即对总就业人数和三次产业产值进行回归，也可以采用单独产业分析法即单个产业就业人数与产值回归。郑琳琳②（2011）分析山西省第三产业发展促进就业增长的实证分析中采用产业比重与就业比重数据进行单独产业就业回归。刘元③（2012）采用最小二乘法（OLS）对总就业人数和三次产业产值进行回归分析。本文借鉴前者经验，结合西藏实际情况，首先采用单独产业分析法，以第三产业就业人数为因变量、第三产业增加值为自变量进行 OLS 回归；其次采用三次产业联动法，以总就业人数为因变量，三次产业增加值为自变量进行 OLS回归。既分析第三产业内部产值对就业的影响，又分析三大产业相互作用下的就业情况。将两者进行对比，分析总结西藏第三产业的实际就业效应大小。
　　
　　一、第三产业增加值与就业人数的回归分析
　　
　　研究第三产业增加值对就业人数的影响，选取回归方程
　　 　　
　　进行分析。其中自变量 Y 为第三产业增加值，因变量 L 为第三产业就业人数，样本区间为 1985-2014 年的第三产业增加值和就业人数（数据来自于《2015 年西藏统计年鉴》）。为了消除异方差带来的影响和解释经济意义的需要，分别对两个变量取对数，得到两个序列 LNL 和 LNY.
　　
　　（一）单位根检验
　　
　　第三产业增加值与就业人数都是时间序列数据，对时间序列进行分析的前提是必须保证序列具有平稳性，对具有非平稳性序列进行回归建模分析会导致伪回归问题。因此在进行回归分析之前，必须要对各个时间序列 LNL 和 LNY 进行单位根检验，判断序列的平稳性。如果序列具有平稳性，就可以进行回归分析，否则要做进一步的处理。
　　
　　进行单位根检验选择 ADF 检验。经过 ADF 检验发现，原序列 LNL 和 LNY的 P 值都远远大于 5%的显著水平，则不能拒绝序列有一个单位根的原假设，即序列 LNL 和 LNY 都不具有平稳性，是非平稳时间序列。此时已经不具备进行OLS 估计的基本条件。我们需要对数据做进一步的处理。将序列 LNL 和 LNY分别进行一阶差分，得到序列 DLNL 和 DLNY.分别对序列 DLNY 和 DLNL 进行 ADF 检验，得到序列 DLNY 和 DLNL 的 P 值分别为 0.0007 和 0.0001,远远小于 5%,应拒绝序列有一个单位根的原假设，即序列 DLNY 和 DLNL 没有单位根，是平稳序列。所以，原序列 LNY 和 LNL 是一阶单整，即 LNY~ D（1），LNL~D（1）。
　　
　　（二）协整检验--EG 两步检验法
　　
　　时间序列具有平稳性是进行 OLS 估计的先决条件，而序列 LNY 和 LNL 不具有平稳性，继续进行 OLS 估计容易出现伪回归问题。协整检验的意义就是验证非平稳序列之间的回归是否是伪回归，即检验变量之间是否存在某种稳定的关系，这种稳定关系就是长期均衡关系。
　　
　　协整检验的前提是原序列是非平稳的，且各序列具有同阶单整。序列 LNY和 LNL 正好满足上述两个条件：LNY 和 LNL 都不是平稳序列；LNY 和 LNL 都是一阶单整。具备做协整检验的条件。
　　
　　进行协整检验的方法一般有 EG 检验法和 Johansen 检验法。这里我们选取EG 检验法。操作步骤大致如下：
　　
　　（1）确认变量是否为同阶单整。如果变量不是同阶单整，不可以进行后面的协整检验。
　　
　　（2）估计协整关系。因为 LNY~ D（1），LNL~ D（1），选用如下模型
　　 　　
　　进行 OLS 估计。
　　
　　（3）检验协整关系。依据步骤（2）可以得到模型 OLS 估计的残差 ε 序列，如果残差序列是平稳的，则单位根变量 LNY 和 LNL 具有协整关系。否则就不存在协整关系。判断残差序列是否平稳最简单的方法依然是使用 ADF 检验。
　　
　　通过上述步骤操作，得到残差序列（下图中的 DU）具有平稳性，具体情况如下图：
　　
　　从图 4-1 可以看出，残差序列在 1%、5%、10%的显著水平上的值都大于 ADF 值，且 P 值为 0.0003,远小于 5%,所以应该拒绝残差有单位根的原假设，即残差序列具有平稳性。因此序列 LNY 和 LNL 具有协整关系，即二者具有长期均衡关系。
　　
　　对序列 LNY 和 LNL 进行长期均衡的 OLS 估计，得到如下方程：
　　 　　
　　由式（4-4）得知，方程的拟合优度很高，达到 0.95,常数项与截距项都通过了统计检验。由于 LNL 和 LNY 具有协整关系，因此式（4-4）的估计结果不是伪回归的结果，估计的系数 0.38 反映了 LNL 和 LNY 具有正相关的长期均衡关系：即第三产业增加值每上升 1%,第三产业就业人数就会上升 0.38%.因此第三产业的发展会促进就业的增长，这一结论与第三章的论证相一致。
　　
　　（三）误差修正模型（VECM）分析
　　
　　上述 EG 检验证明 LNY 和 LNL 存在协整关系，意味着二者存在长期均衡。
　　
　　但是如果考虑短期情况，各个变量可能会偏离长期均衡，围绕长期均衡波动。即变量存在处于长期均衡状态和偏离均衡并逐步恢复到长期均衡状态。而这种向长期均衡的动态调节过程就是误差修正模型研究的内容与意义。
　　
　　根据赤池信息准则（AIC）和施瓦茨准则（SC），确定滞后阶数 p 值的方法与原则是在增加 P 值的过程中，使 AIC 和 SC 同时最小。由于第三产业产值与就业人数是年度数据，滞后阶数一般比较到 P=4.即分别建立一阶、二阶、三阶、四阶滞后模型，比较各个模型的 AIC 和 SC 统计量，并取最小统计量所对应的滞后阶数。结果如表 4-2 所示。
　　
　　由表得出，AIC 与 SC 最小值对应的 P 值均为 1,故 VECM 模型的滞后阶数 P=1.本节估计的 VECM 模型表示如下：
　　 　　
　　其中 ECMt-1=LNLt-1-0.5005LNYt-1-1.4610 是误差修正项。误差修正项反映了变量偏离长期均衡的非均衡误差，误差修正项前面的系数就是调整参数，用于反映变量当期的变化回归到长期均衡或者消除非均衡误差的速度。由式（4-5）和式（4-6）式得知，这里 VECM 模型的误差修正项的系数均为负数，说明偏离非均衡误差会得到修正，符合误差反向调节机制。
　　
　　这里系数估计值各有相应的含义：第一个系数-0.1955 表示，在 LNY 不变的情况下，LNL 在第 t 期的变化可以消除前一期 19.55%的非均衡误差，即第三产业就业人数如果在上一期高出均衡值 1 个百分点，在下一期就会下降 0.1955个百分点。启示我们不能盲目快速增加第三产业就业人数，否则会带来就业效应下降的后果，要按照式（4-4）长期均衡关系下的发展趋势来提高第三产业就业效应。第二个系数-0.1555 表示，在 LNL 不变的情况下，LNY 在第 t 期的变化可以消除前一期 15.55%的非均衡误差，即第三产业增加值如果在上一期高出均衡值 1 个百分点，在下一期就会下降 0.1555 个百分点。同样启示我们，不能为了快速提高第三产业就业效应就盲目增加第三产业产值，以期高产值带来高就业效应，提高第三产业增加值依然要遵循式（4-4）协整关系的长期发展趋势。
　　
　　二、三次产业增加值与总就业人数的回归分析
　　
　　由于第三产业不是孤立存在，要受到第一、第二产业的影响，就业人数在三大产业间也是随意流动的。因此采用三次产业联动法，将三大产业联合起来，与总就业人数进行回归分析。不仅可以考虑到三大产业之间的相互影响，还可以相比较得出哪个产业对劳动力就业的影响最大。选取回归方程
　　 　　
　　其中自变量 Y1 为第一产业增加值，自变量 Y2 为第二产业增加值，自变量Y3 为第三产业增加值，因变量 L 为三次产业的总就业人数。样本区间为1985-2014 年的三大产业增加值和总就业人数。为了消除异方差带来的影响和解释经济意义的需要，分别对各个变量取对数，得到序列 LNY1、LNY2、LNY3和 LNL.
　　
　　（一）单位根检验
　　
　　依照惯例，首先要对序列 LNY1、LNY2、LNY3 和 LNL 分别进行单位根检验。经过 ADF 检验，按照 P 值低于 5%的显著性水平拒绝序列有单位根的原假设，得出原序列 LNY1、LNY3 和 LNL 都不是平稳序列，而 LNY2 是平稳序列。将LNY1、LNY3 和 LNL 进行一阶差分，得到平稳序列，所以 LNY1、LNY3 和 LNL是一阶单整。即 LNY1~ D（1），LNY2~ D（0），LNY3~ D（1），LNL~ D（1）。
　　
　　由于原序列 LNY2 是平稳序列，而 LNY1、LNY3 和 LNL 是一阶单整，不可以直接进行回归分析（否则存在伪回归问题），也不可以进行协整分析（协整分析要求每个序列都是同阶单整）。根据西藏三大产业的具体就业状况，第一、第三产业的就业比重分别超过 40%,而第二产业的就业比重不足 15%,因此分析第二产业对就业影响的意义不大，可以剔除第二产业增加值这一因素。如此，将平稳序列 LNY2 剔除，其他序列都是一阶单整，可以进一步做下面的协整检验。
　　
　　（二）协整检验--EG 两步检验法
　　
　　序列 LNY1、LNY3 和 LNL 都是一阶单整，具备做协整检验的前提条件。检验步骤如前所述，这里仅简单陈述简要过程：
　　
　　首先估计协整关系。因为 LNY1~ D（1），LNY3~ D（1），LNL~ D（1），选用如下模型
　　 　　
　　进行 OLS 估计。接下来检验协整关系。依据式（4-8）模型 OLS 估计得到残差 ε序列，对残差序列进行 ADF 检验。
　　
　　通过上述步骤操作，得到残差序列（下图中的 DU）具有平稳性，具体情况如下图：
　　
　　从图 4-2 可以看出，残差序列在 5%、10%的显著水平上的值都大于 ADF 值，且 P 值为 0.0373,小于 5%,所以应该拒绝残差有一个单位根的原假设，即残差序列具有平稳性。因此序列 LNY1、LNY3 和 LNL 具有协整关系，即三者具有长期均衡关系。
　　
　　对序列 LNY1、LNY3 和 LNL 进行长期均衡的 OLS 估计，得到如下方程：
　　 　　
　　由式（4-9）得知，方程的拟合优度较高，达到 0.91,常数项与截距项都通过了统计检验。由于 LNL 和 LNY1、LNY3 具有协整关系，因此式（4-9）的估计结果不是伪回归，估计的系数-0.16 和 0.22 分别反映了正相关和负相关的长期均衡关系：第一产业增加值每上升 1%,总就业人数就会下降 0.16 个百分点；第三产业增加值每上升 1%,总就业人数就业上升 0.22 个百分点。因此第一产业的发展不仅不会增加就业，反而会减少就业量；而第三产业的发展会促进就业的增长。
　　
　　式（4-9）第三产业就业增长系数 0.22 要小于式（4-4）式中的系数 0.38,这可能与抵消掉第一产业下降的那部分就业量有关，使得总就业量的增长比例要低于第三产业就业量的增长比例。
　　
　　（三）误差修正模型（VECM）分析
　　
　　尽管 LNY1、LNY3 和 LNL 存在长期均衡关系。但是各变量的短期波动情况会如何？下面我们建立 VECM 模型来考虑各变量的短期波动。
　　
　　由于三次产业产值与总就业人数是年度数据，滞后阶数一般比较到 P=4.即分别建立一阶、二阶、三阶、四阶滞后模型，比较各个模型的 AIC 和 SC 统计量，并取最小统计量所对应的滞后阶数。结果如表 4-4 所示。
　　
　　根据 AIC 和 SC 准则，P=1 时二者数值最小，因此这里 VECM 模型的滞后阶段选定为 1.估计的 VECM 模型表示如下：
　　 　　
　　其中 ECMt-1=LNLt-1-2.9036LNY1t-1+1.0998LNY3t-1+0.7057 是误差修正项。
　　
　　误差修正项反映了变量偏离长期均衡的非均衡误差，误差修正项前面的系数就是调整参数，用于反映变量当期的变化回归到长期均衡或者消除非均衡误差的速度。由式（4-10）和式（4-12）得知，这里 VECM 模型的误差修正项系数均为负数，说明偏离非均衡误差会得到修正，符合误差反向调节机制。而式（4-11）的误差修正项的系数为正，意味着非均衡误差得不到修正，且误差会越来越大。
　　
　　这里系数估计值各有相应的含义：第一个系数-0.0106 表示，在 LNY1 和LNY3 不变的情况下，LNL 在第 t 期的变化可以消除前一期 1.06%的非均衡误差，即总就业人数如果在上一期高出均衡值 1 个百分点，在下一期就会下降 0.0106个百分点。启示我们不能盲目快速增加三产总就业人数，否则会带来就业效应下降的后果，要按照式（4-9）长期均衡关系下的发展趋势来提高就业效应。第二个系数 0.0252 表示，在 LNL 和 LNY3 不变的情况下，LNY1 在第 t 期的变化会增加前一期 2.52%的非均衡误差，即第一产业增加值如果在上一期高出均衡值 1个百分点，在下一期就会增加 0.0252 个百分点，这并不符合经济意义。第三个系数-0.0908 表示，在 LNL 和 LNY1 不变的情况下，LNY3 在第 t 期的变化可以消除前一期 9.08%的非均衡误差，即第三产业增加值如果在上一期高出均衡值 1个百分点，在下一期就会下降 0.0908 个百分点。启示我们不能为了快速提高第三产业就业效应就盲目增加第三产业增加值，提高第三产业增加值依然要遵循式（4-9）协整关系的长期发展趋势。
　　
　　三、第三产业就业效应的回归总结
　　
　　本节主要研究第三产业整体就业效应，首先仅对第三产业增加值与就业人数进行回归分析，得到式（4-4）的回归方程：
　　
　　LNL = 1.94 + 0.38LNY
　　
　　系数 0.38 表示第三产业增加值增长 1 个百分点，第三产业就业人数会增长 0.38个百分点。由于三大产业之间具有相互作用，单独进行第三产业增加值与就业人数的回归分析似乎有失偏颇，因此需要对三大产业的增加值与总就业人数进行回归分析，得到式（4-9）的回归方程：
　　
　　LNL = 4.57 - 0.16LNY1 + 0.22LNY3　　
　　其系数 0.22 表示第三产业增加值每增长 1 个百分点，总就业人数就会增长 0.22个百分点。系数-0.16 表示第一产业增加值每增长 1 个百分点，总就业人数会减少 0.16 个百分点。
　　
　　综合两个回归方程，第三产业增加值每增长 1 个百分点，第三产业就业增长0.38 个百分点，但总就业增长只有 0.22 个百分点，说明第三产业吸收了来自第一产业的剩余劳动力。随着经济的发展，第一产业会减少总就业人数，而第三产业会增加总就业人数。因此我们认为第一产业减少的就业人数也就是剩余劳动力会转移到第三产业中。而第二产业由于就业比例较低且时间序列不属于一阶单整，没有参与回归分析。由以上分析得出西藏第三产业的就业吸纳能力最强，不仅自身就业量不断上升，还能吸纳第一产业的剩余劳动力。