多元回归分析是描述多个自变量和一个因变量之间线性关系的分析方法,它根据样本数据估计回归系数(权重)来构建回归方程,从而可以根据多个预测变量(自变量)的数值来预测准则变量(因变量)的数值。如公司根据本城市的新建房面积、新结婚人数和年可支配收人增长数来预测居民楼房销售额。又如预测一年后职工绩效,可以用能力测试成绩、面试分数、工作经历和教育水平等变量。多元回归分析运用多个自变量去预测某个准则变量，较之单一自变量预测，一般说来总是更准确一些。方程中包含的各个变量,应尽可能互不相关，各个变量都独立地对因变量作出贡献。由于多元回归分析的简易性和普适性,其在管理研究中得到广泛的应用。
回归方程的各个变量一般都要求定距和定比尺度,尽管有时可引入定类尺度变量(0,1变量)。自变量与因变量关系的数学表达式为:
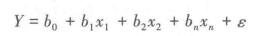
式中,b0为常数,即所有自变量为零时Y的数值;
bi为相应于每个自变量xi的回归系数,代表回归曲面的斜率;
为误差项,正常情况下取值按均值为0分布,计算时一般可设为0。
回归系数可以是原值bi,(即x的实际值) ,也可以是标准化后的数值,标准化后的回归系数一般用
表示。不论是原值还是标准化值，回归系数都表示x变量每变化一个单位,Y相应的变化值。标准化后的系数
具有权重的含义,表示各x变量相对的重要程度,如
=0.60,
=0. 30,则表示X1对Y的影响是X2的两倍。但采用原值的情况下,各回归系数bi,值的大小不能说明变量对Y的相对影响大小。
现举例说明。
算例 某企业预测电子商务网站用户数,选择成本速度比(X1)、安全性(X2)、可靠性(X3)作为自变量。
利用统计软件SPSS处理该回归方程。SPSS和其他统计软件一样,提供选择自变量的方法,变量筛选一般有两种途径,一种是较通用的逐项添加法,从一元回归分析开始,逐步加入那些引起相关系数
增幅最大,对因变量最有解释意义的自变量。另一种是消去法,先构建研究者认为重要的多个独立变量的回归方程,然后从中删去那些引起
变化最小的变量。
逐步添加法的计算过程用一个算例来表示(表5-18)。
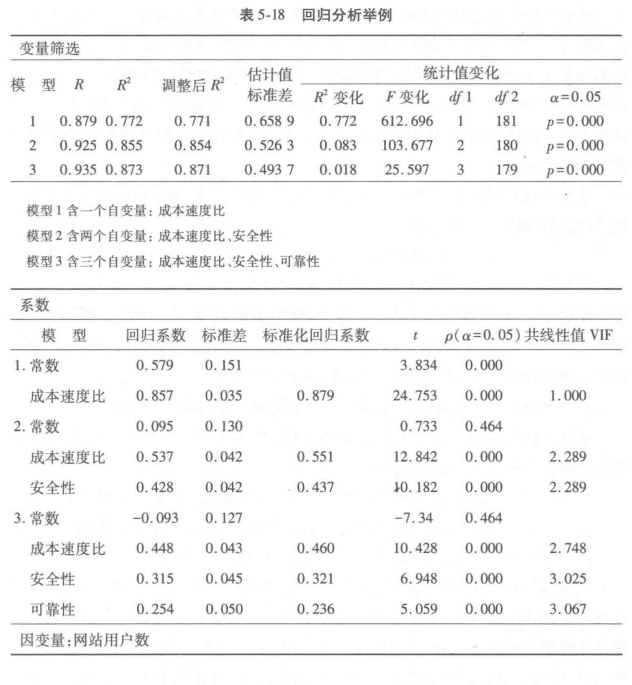
表5-18中的变量筛选部分,表明有三个模型。模型1引入第一个变量,成本速度比。模型2加入安全性变量,模型3再加上可靠性共三个变量。从表中可以看出,模型1调整后的
=0.771,表示成本速度比这个变量与因变量用户数的协同变异部分占77.1%。模型2引入安全性变量后,两个变量的协同变异部分提高到85.4%。模型3加上可靠性变量后只提高约2% ,协同变异部分达到87.1%。
对表中的数据作几点说明:
①调整后
。调整
的目的,是使该
与自变量个数不同的其他模型具有可比性,变量个数越多,调整下降幅度越大,如模型3的
从0.873降到0.871。
②标准差σ。表示Y的实际值与按回归方程估计的9值的标准差。如模型3的标准差σ=0.493 7。
③方差分析用来判断方程中的一组回归系数,从整体上看是否偏离0,F临界值从附表3查出,分子的自由度为k,即自变量的个数,本例分别为(1,2,3),分母自由度为n-k-1,n即样本数(观察值),本例为183, 故对于模型3,自由度df=183-3-1=179。显著度a=0.05时,查附表3得知,F的临界值为8.55,表5-18中算出的F值均大于临界值,且概率均小于0.05,说明统计检验支持回归系数偏离0。
④表5-18的第二部分表示三个模型的回归系数。“b” 表示由原始x值估计出的回归系数,模型3的数学表达式为:
Y =-0.093 + 0.448X1， + 0.315X2 + 254X3 +e
⑤"β"列表示标准化后的回归系数。标准化后,常数项即回归线截距为0。一般情况下,各变量都是按不同尺度赋值，标准化后的β表示各个自变量对因变量解释能力的相对贡献,使各回归系数之间具有可比性。本例中，成本速度比较之其他两个变量解释能力要大(0.46>0. 321 ,0. 236)。
⑥每个回归系数都有标准差，衡量每个回归系数的样本变异状况。
⑦“t”列表示各回归系数的显著性检验值,按各变量的自由度查附表,三个自变量的系数值统计上都显著偏离0。
表5-18的回归方程表示因变量网站用户与成本速度比、安全性和可靠性等自变量之间的关系,回归系数按整体和个别统计检验结果,其值都显著偏离0。其中,成本速度比对客户量影响最大,后面顺次为安全性和可靠性。
有些回归方程中,自变量之间相关性较强,影响多元回归分析的效果,使得不同的样本，估计出的系数波动较大,用系数来表示各变量的权重就不可靠。可接受的自变量相关程度是多少，要看情况而定，如果相关系数达到0.8以上,应加以处理,或者从两个相关变量中删去一量，或者引人一个能代替这两个相关变量的新变量。统计表5-18中有一列“共线性值VIF”即变量贬值指标,它测量其他自变量对该回归系数的影响，此值如等于或大于10,则看作存在共线性( collinearity,mulicollinearity) ,本例中该值均远小于10,不存在该问题。
