第 4 章 中国纺织品出口贸易隐含碳估算
本文采用投入产出法来评估中国纺织品出口贸易隐含碳。
4.1 估算方法简介
4.1.1 投入产出法的产生
投入产出法是在一定经济理论的指导下,通过编制投入产出表,运用线性代数方程,建立投入产出模型,综合分析和确定国民经济各行业部门之间、再生产各环节之间数量依存关系的一种经济数量分析方法。用投入产出法测算产品生产过程中的碳排放,主要是基于一国的投入产出表,以生产行业或者部门为单位,并涵盖了各个行业之间的关系。其特点是在考察各行业部门间错综复杂的投入产出关系时,能够发现任何局部的最初变化对经济体系各部分的影响。
4.1.2 投入产出法的发展与运用
到目前为止,投入产出法无论在理论上,还是在实践上都有了很大的发展和进步,取得了丰富的成果。其从早期的静态的投入产出模型到随着研究的不断深入,幵发了动态的投入产出模型。近年来,随着投入产出法与数量分析等经济方法的结合,投入产出分析应用范围更加广泛。目前,投入产出分析法已经拓展到经济研究领域的各个方面:为编制经济计划特别是中长期计划提供依据;分析经济结构,进行经济预测;研究经济政策对经济生活的影响;研究污染、人口、就业及收入分配等专门的社会问题。(何丹丹)最先运用投入产出法的是以列昂惕夫为代表的学者,他们将投入产出分析法应用到区域经济建模中,丰富了区域经济学的研究方法,并在国家投入产出模型的基础上逐渐开发了区域投入产出模型和区域间投入产出模型。Chenery(1995)和 Moses(1995)先后独立提出了多区域投入产出模型,也被称为 Chenery-Moses模型或列系数模型,并得到了广泛的应用。2008 年,齐哗等引入投入产出模型对中国进出口贸易的隐含碳进行了测算,此后,该模型在国内得到了广泛的应用。
单区域的投入产出模型(SRIO),此模型采用单个国家的投入产出表来评估贸易隐含碳,然而由于各个国家的技术水平不同,因此若采用此模型会造成评估结果偏离真实水平。针对这一弊端,近年来学术界提出了双边贸易模型以及多区域贸易模型,并获得了广泛的应用。多区域的投入产出分析模型(MRIO)由于可以很好的反映不同国家地区的技术水平差异,相对于技术同质性假设,可以明显的提高测量的准确度。[23]
4.1.3 投入产出表构成
目前的投入产出表分为静态价值投入产出表和非竞争型的投入产出表,区别在于是否将中间投入部分分为国内中间投入和进口中间投入。[24]
4.1.3.1 静态价值投入产出表【1】

中国投入产出学会发布的中国投入产出表(1990 年、1992 年、1995 年、1997年、2000 年、2002 年、2005 年、2007 年、2010 年),其结构类型可归纳为竞争型的投入产出表,从编制 1987 年全国投入产出表开始,中国投入产出表的编制工作开始规范化,确定每逢 2、7 年份编制基本表,逢 0、5 年份编制延长表。陈曦(2011 年)用中国的投产表(2002 年、2005 年、2007 年)测算了三年中国的进出口贸易隐含碳,结果显示隐含碳出口及净出口的绝对数量增长较快,表明中国在贸易顺差扩大的同时向国内转移了大量的 CO2排放。中国的投入产出表虽然数据年限有 1990 年到 2010 年,但其中年度数据的行业数据方面会有缺失,且该投入产出表的行业分类与海关统计年鉴的贸易数据行业分类并不完全一致,在计算时需要对两个表的行业进行分类,使其行业分类一致。若要用此表进行计算,难度较大且结果会有所偏失。静态价值投入产出表并没有区分国内中间投入和进口中间投入,本文所要测算的纺织品贸易隐含碳,由于中国纺织品是一个进口中间品占很大比例的行业,因此若要用中国投入产出学会的投入产出表估算出口贸易隐含碳,计算繁琐且误差较大。
4.1.3.2 非竞争型投入产出表针对静态投入产出表的弊端,本文对纺织品贸易隐含碳的估算有必要采用非竞争型投入产出表。非竞争型投入产出表由于研究范围不同分为两种形式。一种是基于 SRIO 模型的投入产出表,另一种是基于 MRIO 模型的投入产出表。【2】
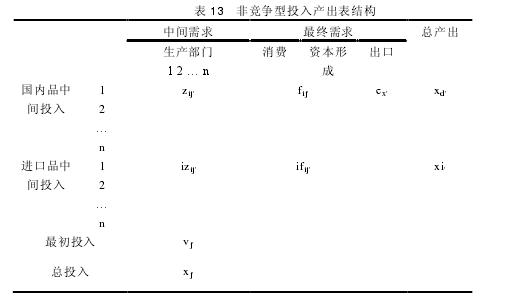
上表为基于 SRIO 模型的非竞争型投入产出表,可以看到与表 12 静态价值投入产出表最大的区别在于中间投入的划分,非竞争型投入产出表将中间投入区分为国内中间品投入和进口中间品投入,体现了两者的不完全替代性,考虑到了贸易中的进口中间品对国家投入产出的影响。
基于 MRIO 模型的非竞争型投入产出表综合考虑了各个国家之间的投入产出关系,便于分析多区域的投入产出关系。
4.2 基于投入产出法对中国纺织品出口贸易隐含碳的估算
本文引入当前学术界主流的贸易隐含碳评估方法——投入产出法估算1995-2011 年中国纺织品贸易隐含碳。
本章节主要包括以下几部分,首先简单介绍了贸易隐含碳的估算流程;其次是所需数据的来源及处理;最后是计算的具体步骤及结果。
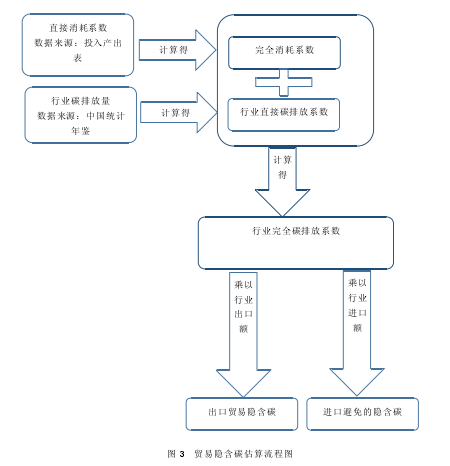
4.2.1 计算流程
运用投入产出法估算贸易隐含碳,第一步,需要整理得到直接消耗系数,在其基础上运算得到完全消耗系数;第二步,得到各行业的直接碳排放系数,与前面得到的完全消耗系数整理运算得到行业的完全碳排放系数;最后,在已知行业贸易额的基础上,计算出贸易隐含碳。
采用投入产出法评估贸易隐含碳,需要知道的数据有投入产出表、行业的碳排放量以及贸易出口额。【3】
根据投入产出表,A表示为直接消耗系数,其元素aij表示第j部门生产单位产品对第i部门产品的直接消耗量,称为第j部门对第i部门产品的直接消耗数。其反映了两部门间的技术经济联系,又称技术系数。
为了提供一单位的最终产品,其本部门的消耗为X0=I根据直接消耗系数的概念,为了提供单位最终产品,需要消耗其他各部门的产出为X1=A而为了提供I1的产品,又需要消耗N个部门的产出为X2=A* X1=AA以此类推,为了提供一单位的最终产品,其在整个生命过程中的完全消耗为X= X0+X1+ X2+…=(I-A)-1(4-1)其中I为单位矩阵,A为直接消耗系数,完全消耗系数,即(I-A)-1反映了为获得单位最终产品对各部门总产出的需求量,包括直接需求,间接需求和最终需求。
在产品的生产过程中,一部分产品作为中间投入被消耗掉,而这一部分产品的生产也排放了CO2,所以不能直接以最终产品作为碳排放的核算标准,而应该采用最终产品所对应的总产品来测算碳排放。
将投入产出模型扩展到非经济领域,用来衡量单位产出变化所产生的外部性。本文引入行向量c,即直接碳排放系数,它的元素表示j部门每单位产出的直接CO2排放量,所以完全碳排放系数可以表示为C=c(I-A)-1(4-2)对于贸易隐含碳的估算,完全碳排放系数与出口额的乘积即为出口贸易隐含碳,对于纺织品来说出口额远大于进口额,且估算出口贸易隐含碳更具有意义,同时由于进口隐含碳的计算过于复杂,因此本文并没有深入研究。
4.2.2 数据来源及处理
本文利用国内投入产出表计算 2010、2011 年中国纺织品贸易中隐含碳排放量,需要使用中国的投入产出表、分行业的能源统计数据以及分行业的贸易数据。
由于这些数据对商品分类标准不一致,本文需先进行重新分类处理才能用其进行计算。
4.2.2.1 数据来源本文研究中国纺织品出口贸易隐含碳及其影响因素所需要的数据有:中国的投入产出表、中国贸易的进出口商品分行业金额、各行业部门能源消费量、各行业部门总产值、各种能源的二氧化碳排放系数。其中中国贸易中进出口商品分类金额数据来源于 WIOD 数据库(1995-2009),《中国统计年鉴》(2010-2011);中国流量矩阵表来源于 WIOD 数据库(1995-2009),《2010 年中国投入产出表》;各行业不同能源消费总量、各行业总产值来源于 WIOD 数据库(1995-2009)、《中国统计年鉴》(2012-2013);中国能源消耗数据来源于《2010 年中国统计年鉴》。
4.2.2.2 行业分类与整合从国内的数据可以看到,不同的数据来源于不同分类的统计表,其对于商品的分类方法也不完全相同。例如,《2010 年中国投入产出表》将产品分为 42 个部门,而《2012 年中国统计年鉴》中能源消费账户将产品分为 52 个部门。因此,研究中首先要就这几种不同统计口径的分类进行整合归并,建立一个相对可比较的分类系统。[25]
经过对《2010 中国投入产出表》和《2013 年中国统计年鉴》的按行业分能源消费量表的观察发现投入产出表 42 部门分类和能源消费量表 52部门非常好的对应关系。根据《国际标准产业分类》修订本第 2 版与第 3.1 版的对应表将其合并整理得新的行业分类。如表 14 所示,将投入产出表的 42 部门和统计年鉴的 52 部门归类合并为新的 16 个部门。在此分类过程中,因为计算过程更多的依托于投入产出表,因此有统计年鉴几部门是对应投入产出表来进行归类的,在此借鉴了其他学者的一些分类标准。[27]
4.2.2.3 数据处理中国的统计年鉴产出、贸易数据单位为亿元,而 1995-2009 年 WIDO 数据库数据的产出、贸易数据为百万美元,因此需要将 2010 年、2011 年数据转化为百万美元,根据《中国统计年鉴》查得 2010 年、2011 年人民币兑换美元汇率。
在价格指数平减方面,1995-2009 年的现价价总产出、现价中间投入、现价最终需求、现价增加值及现价贸易数据根据不同行业的价格指数进行了处理,2010 年、2011 年相关数据仅用总价格指数进行了处理。
4.2.3 计算过程及结果
4.2.3.1 直接消耗系数计算首先,第一步需要计算各个部门的直接消耗系数表。直接消耗系数,是指各个部门单位产值所需要的其他部门的中间投入量。
直接消耗系数:aij=zij/xj(I,j=1,2,…,n) (4-3)aij表示 j 行业生产单位产品对第 i 行业产品的消耗量,称为第 J 行业对第 i行业的直接消耗系数。aij反应了两行业间的技术经济联系,又称为技术系数。【4】
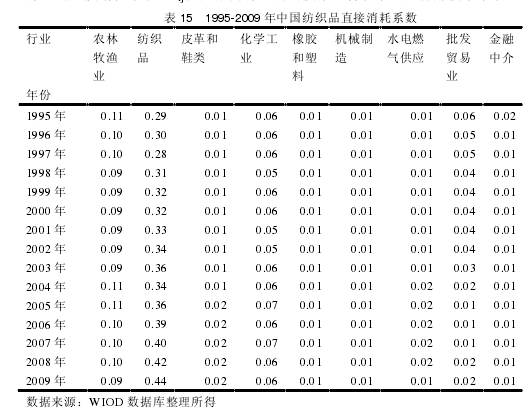
如表 15 所示,列出了 1995-2009 年中国纺织品的部分直接消耗系数,从中可以看到,纺织品除了要消耗自身行业,对其他行业也有较大的消耗。对农林牧渔的消耗一直维持在 0.1 左右,自身行业的消耗呈逐年递增趋势。从上表可出看出,除了纺织品本身,农林牧渔业和化学工业也对纺织品的产出也有着巨大的贡献。【5】


由于中国的投入产出表五年编制一次,因此 2010 年的投入产出表为最新数据,又由于短时间内行业结构并不会发生太大变化,因此在估算 2011 年相关数据时,采用的是 2010 年投入产出表。从表 16 可以看到,除自身行业外,对 2010年中国纺织品产出有着突出贡献的行业为农林牧渔业、化学工业,其直接消耗系数均超过了 0.1。
4.2.3.2 完全消耗系数的计算根据投入产出模型,矩阵 A 是直接消耗系数,它反映了经济中各部门之间的生产联系,这些联系是通过中间投入或中间消耗发生的。
为满足本行业一单位需求,其本行业直接的消耗量为X0=I根据直接消耗系数的经济含义,为了满足本行业一单位的最终产品,需要间接消耗其他行业的产出为X1=A而为了提供数量为 X1的产品,在生产过程中又要消耗 n 个行业的产品为X2=A*A…以此类推,为了提供本行业单位数量的产品,在其整个生命周期过程中的直接消耗和间接消耗为:【6】
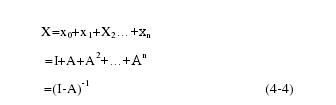
公式(4-4)中的(I-A)-1被称之为完全消耗系数矩阵,表示为了获得本行业每单位需求,各行业总产出随之变动多少单位。
完全消耗系数的意义在于它不仅反映了国民经济各部门之间直接的技术经济联系,还包含了国民经济各部门之间间接的技术经济联系,并通过线性关系,将国民经济各部门的总产出与最终使用联系在一起,从而更加全面深刻的反映了部门之间相互依存的数量关系。【7】
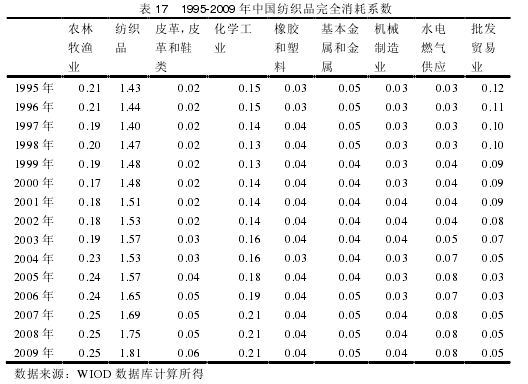
如表 17 所示,纺织品自身完全消耗呈现逐年增加趋势,由最初 1995 年的1.43 增加到 2009 年的 1.81,说明纺织品消耗自身的比例在渐渐增大,在其他行业对纺织品完全消耗的影响中,农林牧渔业并没有太大变化,化学工业的贡献度有增大趋势,而批发贸易业的贡献度则有下降趋势。在其他行业中,农林牧渔业对其影响最大,纺织品每单位产出需要完全消耗其 0.2 单位左右。【8】

国内的投入产出表为 5 年编制一次,所以目前所能得到的最近投入产出表数据为 2010 年投入产出表,由于短时间内行业结构并不会发生明显变化,因此可以用 2010 年的投入产出表来计算 2011 年的相关数据。
4.2.3.3 直接碳排放系数行业的直接碳排放系数,即该行业每生产一单位产值,需要排放的二氧化碳量。
WIOD 数据库给出了 1995-2009 年中国 35 行业的直接碳排放量,因此行业的直接碳排放系数的计算就较为简单。而国内的能源数据库提供了部门的能源消耗量,因此需要根据每种能源的碳排放系数,计算出其行业的直接碳排放量。
C=θ1*x1+θ2*x2+θ3*x3+...+θkxk+... (4-5)公式(4-5)中,C 即为部门的直接碳排放量,其中 θk表示部门第 k 种能源的 CO2排放系数,xk表示部门的第 k 种能源消耗量。【9】
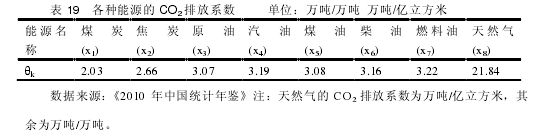
通过表 19,结合国内的能源账户数据,就可以计算得到 2010、2011 年国内的碳排放相关数据。由表 20 和表 21 可以看到,纺织品的直接碳排放系数在中国各行业处于中游地位,远远低于电力等行业,且纺织品的直接碳排放系数呈现逐年下降趋势,由1995 年的 0.53 KG/$下降到 2009 年的 0.07 KG/$。【10】

4.2.3.4 完全碳排放系数在产品的生产过程中,一部分产品作为中间投入被消耗掉,而这一部分产品的生产也排放了 CO2。所以不能直接以最终产品作为碳排放的核算基础,而应该采用最终产品所对应的总产品来测算碳排放。
因此,在已知最终产品与总产品的关系式基础上,可以得到行业完全二氧化碳排放系数为:C=c(I-A)-1(4-6)其中,c 为行业的直接碳排放系数矩阵,其为 1*n 的行向量,其元素表示的意义为行业每 1 单位产出所排放的二氧化碳量。
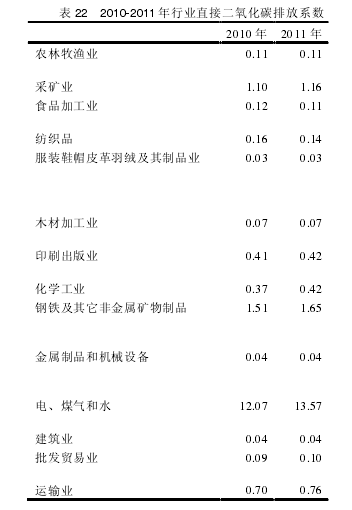
通过上述计算方法,我们可以得到 1995-2011 年各行业的完全二氧化碳排放系数,其中 1995-2009 年的结果是采用 WIOD 数据库计算所得,2010-2011 年的结果是采用《2013 年中国统计年鉴》的数据所得。如表 23、表 24、表 25 所示,在中国行业完全二氧化碳排放系数表中,排在第一位的行业是水电燃气供应业,其完全碳排放系数远远高于其他行业,纺织品的完全碳排放系数居于中游水平。
4.2.3.5 出口贸易隐含碳的估算对于中国纺织品进出口贸易来说,其出口贸易隐含碳是贸易隐含碳研究的重点问题,一是由于中国纺织品的巨额贸易顺差,另一原因就是中国纺织品的产业结构,成为发达国家碳减排的避风港,因此本文重点研究中国纺织品出口贸易隐含碳。
EC= c(I-A)-1EX (4-7)其中,EC 为中国纺织品出口贸易隐含碳,EX 为中国纺织品出口贸易额。【11】
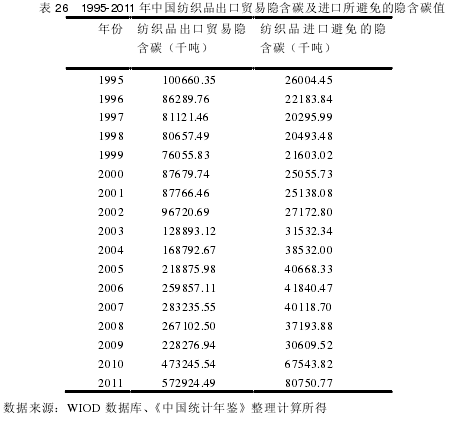
如表 26 所示,可以看到中国纺织品出口贸易隐含碳要远远大于进口所避免的隐含碳,因此可以判断中国纺织品是隐含碳出口部门,近几年中国纺织品出口贸易隐含碳总体呈增加趋势,到 2009 年,中国纺织品出口贸易隐含碳比 1995年上涨 469.17%,同期纺织品出口贸易隐含碳与进口隐含碳差额 197667.42 千吨,可见中国纺织品的出口为发达国家承担了相当一部分碳排放责任。4.3 估算结果分析利用前文所述的计算方法,分别计算中国纺织品出口产品的完全碳排放系数、贸易隐含碳以及纺织品进口所避免的隐含碳,并且对计算结果分行业分析。
在前面估算纺织品贸易隐含碳的过程中,本文可得到如下 4 点结论。
第一,中国纺织品的直接消耗系数与完全消耗系数相差较大,说明纺织品在其生产过程中,消耗了很大一部分其他行业的产出,而这部分产出在生产过程中也要排放二氧化碳气体因此在估算其隐含碳的过程中,不能仅仅关心自身行业所排放出的二氧化碳,需要以纺织品的完全消耗来作为估算标准。
第二,观察中国各行业的完全碳排放系数,其中纺织品居于第 9 位,排在第1 位的是电、煤气和水供应业,且与其他行业有着较大差距,其完全碳排放系数是纺织品的 8 倍左右。纺织品的完全碳排放系数均大于直接碳排放系数,并且差距很大,从 1995 年两者相差 5 倍到 2011 年相差 46 倍之多,这说明纺织品行与其他行业的关联度逐渐增加,生产产品中隐含的二氧化碳中所间接隐含的其他行业所生产二氧化碳的比例越来越高。中国纺织品的直接碳排放系数呈几何倍数下降,但其完全碳排放系数并没有显着变化,这说明纺织品生产过程中自身行业所排放的二氧化碳较低,但却需要消耗大量高排放的原材料,造成了其完全碳排放系数并没有显着下降,且维持在较高水平。
第三,中国纺织品出口贸易隐含碳数额巨大,仅次于电气光学设备业、基本金属和金属业,占总贸易出口贸易隐含碳的十分之一左右。从中国纺织品贸易隐含碳数据可以看到,中国纺织品是隐含碳净出口产业,且其数额相差巨大,因此,分析中国纺织品贸易隐含碳就具有重要意义。
第四,在估算纺织品隐含碳的过程中,可以得到其相近行业—皮革和鞋类数据,比较分析可得,行业规模方面,在行业总产出、进出口方面,皮革和鞋类的数值要远远低于纺织品的,可见纺织品在中国经济发展中的地位要高于皮革和鞋类业。【12】
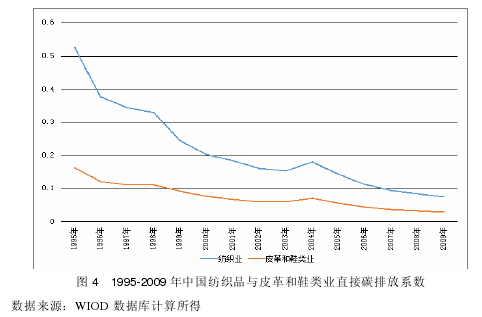
由图 4 可以看到,皮革和鞋类业的直接碳排放要低于纺织品的,说明皮革和鞋类业要更加环保,单位产值所排出的二氧化碳要低于纺织品,观察其长期趋势,随着时间的推移,两行业的直接碳排放系数虽然仍有差距,但其差距在逐渐减少,主要原因是纺织品的直接碳排放系数降低的很迅速,说明中国加大了纺织品的减排力度,并起到了很好的效果。【13】
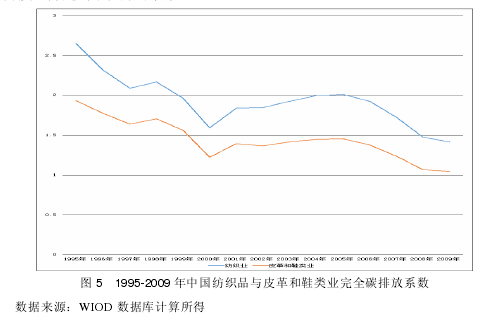
由图 5 可以看到,中国纺织品与皮革和鞋类业完全碳排放系数有着类似的变化趋势,且其差距并没有明显的变化,这是因为纺织品不仅消耗自身行业,还需要消耗大量其他行业的资源,这提高了纺织品的完全碳排放系数,因此导致纺织品与皮革鞋类业的完全碳排放系数差距没有直接碳排放系数差距那样有着明显的减少。





