5.6 假设检验:结构方程模型分析。
Karl Joreskog 和 Dag Sordorm 在 20 世纪 70 年代提出结构方程模型(structure equation modeling,SEM)是应用线性方程表示观测变量与潜变量之间的关系以及潜变量之间关系的一种统计分析方法,试图通过实验数据验证理论模型假设中潜变量之间的关系,结构方程模型通过结合路径分析及因素分析的方法对观测变量与潜变量之间的关系进行验证,最终得出自变量与因变量之间的总体效应、直接效应及间接效应。结构方程模型主要用于检验理论模型与样本数据之间的匹配度。结构方程模型的应用软件很多,且各有特点,这些软件包括Lisrel(Linear Structural Relations) 、 AMOS(Analysis of MomentStructures)、EQS(E-quations)和 Mplus 等。本研究中采用的是 AMOS 软件对数据进行分析。结构方程模型通常包括测量模型和结构模型两种模型,其中测量模型描述的是潜在变量经由观测指标如何经过测量或概念化形成的,潜在变量和观测变量之间的关系共同构成了测量模型概念的内涵;而结构模型主要描述的是潜在变量之间的相关关系及模型中无法解释的变异量。本研究采用的是结构模型,实际上包括了测量关系和结构关系两种关系。
在结构方程模型中,结构模型主要用于处理潜变量之间的相关关系,方程中包含三种随机变量:观测变量、潜变量及误差变量。通过对外生变量、内生变量及中介变量进行区分厘清变量之间的结构关系。结构方程模型可以通过矩阵方程式和路径图两种方式反映各变量之间的测量关系及结构关系,采用矩阵方程式的形式来反映模型关系如下所示:
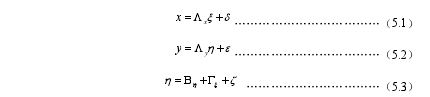
5.6.1 模型识别。
模型识别主要是通过模型拟合过程中的参数数目及可获得的数据资料反映模型是否具有可操作性以及是否能够得到合理的结果。模型识别包括恰好识别、过渡识别和识别不足三种情况,可用模型自由度(DF)来鉴别模型识别情况,当DF<0,模型为识别不足;DF=0,模型为恰好识别;DF>0 模型为过渡识别。本研究中采用自由度来对模型进行识别:Degrees of freedom = 512 >0,因此模型属于过渡识别,可以进行下一步分析。
5.6.2 模型拟合。
模型拟合实际上就是对模型进行参数估计的过程,通过将收集到的样本数据代入理论模型中,对模型参数进行求解,在此过程中,本研究考虑到变量的属性及样本数据的分布特征决定采用最大似然法对参数进行估计。
从模型拟合输出结果中 P 值一栏可以看出五条假设的 C.R.的绝对值均大于1.96,且显著性水平均小于 0.05,因此创业意识、创业品质、创业知识、创业能力及创业态度对创业意愿均有显著的正向影响。
5.6.3 模型评价。
学者 Hair 等人(1998)建议在检验理论模型与样本数据的适配度之前,应先检验模型参数估计是否有下列违规的现象存在:有无负的误差方差存在、标准化参数系数是否大于等于 1、是否有太大的标准误存在;结构方程模型评价使用适配统计量来评估理论模型与样本数据的适配度。整体模型适配度指标分为三类:(1)绝对拟合指标,用来检验理论模型与样本数据的拟合程度,例如卡方值、卡方自由度比、RMSEA、 GFI、 AGFI、 ECVI 等;(2)相对拟合指标,通过将待检验的建设理论模型与基准线模型的适配度进行比较,用以判断模型的契合度,其中相对拟合指标包括 NFI、RFI、IFI、NNFI、CFI 等;(3)简约拟合指标,是绝对拟合指标与相对拟合指标的派生指标,包括 AIC、PNFI、PGFI 和 CN 值。
模型评价指标包括绝对拟合指标、相对拟合指标、简约拟合指标,选取以下指标作为模型拟合结果的评价指标。
绝对评价指标中通过卡方值的 P 值的大小来检验模型,当 P 值大于 0.05 时,不显著的卡方值表明模型与样本数据的不一致可能性较小,认为模型拟合效果良好,但是由于卡方值受自由度与样本数据量的影响较大,自由度越大,卡方值越大,样本量越大,卡方值越大,本研究中自由度为 512,且样本数据量为 779,在这两种情况下卡方值容易达到显著水平,进而增大了拒绝理论模型的概率,因此在实践中通常结合绝对拟合指标、相对拟合指标及简约拟合指标等综合考虑模型的真实拟合效果,从评价指标中可以看出除 P 值外,各项评价指标均达到推荐值的范围,表明模型拟合效果良好。
5.7 调节效应检验。
调节效应检验要根据自变量、调节变量的类型不同采用不同的处理方法,调节变量有分类变量和连续变量两种,对自变量和因变量的关系强弱进行调节,本研究中调节变量包括创业氛围(连续变量)和性别(分类变量)两种,下面对调节变量进行检验。
5.7.1 创业氛围调节效应检验。
调节变量属性为连续变量的潜变量,本研究选取无约束方法进行分析,具体步骤:第一步,将所有潜变量的观测指标进行中心化处理;第二步,对观测指标按照信度进行大小排序,将创业素质变量和创业氛围的交互项按照对应的观测指标相乘得出;第三步,对自变量和调节变量的交互项的影响进行显著性检验,若达到显著水平,则说明调节效应显著。
将创业意识、创业品质、创业知识、创业能力、创业态度、创业氛围以及相应的交互项建立与创业意愿的结构方程模型,对模型进行拟合,检查交互项路径系数及其显著性水平,以此判断调节效应是否显著。
(1)创业氛围在创业意识与创业意愿的影响关系中具有显著的调节作用,创业氛围与创业意识交互作用路径系数为 0.493,显著性小于 0.05,即随着创业氛围越来越浓厚,个体创业意识越强,个体的创业意愿就越高。
(2)创业氛围在创业品质与创业意愿的关系中调节作用不显著,创业氛围与创业品质交互作用路径系数为-0.011,但是未达到显著性水平,因此创业氛围调节作用不成立。
(3)创业氛围在创业知识与创业意愿的关系中调节作用不显著,创业氛围与创业知识交互作用路径系数为-0.055,但是未达到显著性水平,因此创业氛围调节作用不成立。
(4)创业氛围在创业能力与创业意愿的关系中调节作用不显著,创业氛围与创业能力交互作用路径系数为-0.041,但是未达到显著性水平,因此创业氛围调节作用不成立。
(5)创业氛围在创业态度与创业意愿的关系中调节作用不显著,创业氛围与创业态度交互作用路径系数为-0.060,但是未达到显著性水平,因此创业氛围调节作用不成立。
5.7.2 性别调节效应检验。
本研究采用 Spss17.0 软件对数据进行回归分析处理,第一步:将创业意愿作为因变量引入;其次将创业素质、性别及创业素质与性别的交互项作为自变量引入;最后对交互项的显著性进行检验。
从性别调节效应检验结果中可以看出模型 2中调整R2值为 0.377 大于模型1中调整 R2值 0.364,表明模型 2 解释的方差变异大于模型 1 中解释的方差变异,因此性别对创业素质与创业意愿的关系具有调节作用,同时从相伴概率结果看出Sig.F 更改值均小于显著性水平 0.05,表明性别对创业素质与创业意愿有显著的调节效应。
从表中结果可以看出回归模型的显著性为 0.000,达到显著性水平,表明回归模型有显著的统计意义。
从表中结果可以看出:
(1)性别对创业意识与创业意愿的关系具有显著的调节作用,性别与创业意识交互作用路径系数为-0.181,显著性为 0.006 小于 0.05,达到显著性水平,起到负向调节作用,男性为 1,女性为 2,因此男性创业意识对创业意愿的影响高于女性。
(2)性别对创业品质与创业意愿的关系调节作用不显著,性别与创业品质交互作用路径系数为 0.073,显著性为 0.395 大于 0.05,未达到显著性水平,因此性别对创业品质与创业意愿有显著调节作用不成立。
(3)性别对创业知识与创业意愿的关系调节作用不显著,性别与创业知识交互作用路径系数为 0.136,显著性为 0.065 大于 0.05,未达到显著性水平,因此性别对创业知识与创业意愿有显著调节作用不成立。
(4)性别对创业能力与创业意愿的关系调节作用不显著,性别与创业能力交互作用路径系数为 0.010,显著性为 0.895 大于 0.05,未达到显著性水平,因此性别对创业能力与创业意愿有显著调节作用不成立。
(5)性别对创业态度与创业意愿的关系具有显著的调节作用,性别与创业态度交互作用路径系数为-0.152,显著性为 0.048 小于 0.05,达到显著性水平,起到负向调节作用,男性为 1,女性为 2,因此男性创业态度对创业意愿的影响高于女性。





