多元统计分析论文范文第六篇:多元统计分析在区域经济发展中的预测研究
摘要:传统分析方法在解决区域经济发展预测中,容易出现信息丢失的情况,导致人均GDP和GDP增长率的预测结果存在偏差,因此提出多元统计分析在区域经济发展中的预测研究。首先对多元统计分析进行概述,建立区域经济发展预测模型,运用多元统计分析筛选影响因子,输入指标完成区域经济发展预测。模拟预测结果显示,运用多元统计分析的预测方法与传统预测方法相比,人均GDP和GDP增长率预测结果的平均绝对百分比误差低,提高了区域经济发展预测的准确度。
关键词:分多元统计分析;区域经济发展;预测;平均绝对百分比误差;
0 引言
区域经济发展中的历史数据与当下的统计调查数据信息极为复杂[1],包含多个对于经济发展的影响程度不同的因素,但由于它们相互关联、相互影响,关系较为复杂,寻找到客观全面地反映经济发展的因素就十分困难,传统分析方法在处理复杂问题时顾此失彼,易丢失信息导致预测精度不足[2].多元统计分析的特点恰好解决了这一问题。多元统计分析可以对多种变量进行一次性分析处理,能够反映可控变量对因变量的影响程度,从而进行主次因素的区分,提高了复杂问题的解决能力。

1. 多元统计分析概述
在回归方程中,可控变量数值的变化可以影响因变量,通过这种性质,可以实现对因变量的预测,还可以对可控变量进行分析,得出对因变量影响较大的变量,以辨别主次,方便后续问题有针对性地处理。多元线性回归的一般方程为:
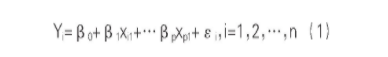
式中,xi1、xi2、…xip,依次为第i次的观测变量x1,x2,…xp的取值,因变量Y的观测值为Yi,β1、β2、…βp表示未知参数。假设εi(i=1,2,…,n)之间均互相独立,同时都遵循同一正态分布N(0,σ2),表示未知参数。多元线性回归通常要对方程中的β0,β1,…,βp和σ2进行估计,同时对已经建立好的多元线性回归模型进行检验,检验内容包括参数与设定,当参数与设定符合一定标准时,该模型方可使用。
2. 多元统计分析在区域经济发展中的预测研究
2.1 建立预测模型
首先,进行序列预处理。将GDP序列记为{Yt},检测{Yt}的平稳性与随机性,经过R语言拟合得出{Yt}的时序图可知实际GDP增长趋势十分明显,表示{Yt}并不是平稳的,此时为使{Yt}平稳化,将{Yt}进行取自然对数与一阶差分处理,记作{荦ln Yt},仍以R语言拟合,所得结果可知,{荦ln Yt}依然存在上升趋势,故继续对其一阶差分处理,同时记为{荦2ln Yt},仍以R语言拟合,可知,{荦2ln Yt}已无显著上升趋势,初步认定{荦2ln Yt}平稳。以语言分别检验{荦ln Yt}、{荦2ln Yt}的ADF单位根,根据相关资料显示初始t统计量为-2.3632,二次差分处理后为-4.8089.{荦ln Yt}ADF单位根检验的值为0.4329,{荦2ln Yt}ADF单位根检验的p值远小于0.1,因此判定对{Yt}进行取自然对数并二次差分处理后的{荦2ln Yt}平稳,即模型参数d=2.
其次,进行模型定阶与参数估计。为了更精准地确定模型阶数p、q,本研究选用AIC与BIC准则:

非中心化模型的k=p+q+1,中心化模型的k=p+q,为使模型最优,取AIC与BIC函数值为最小。以R语言对{荦2ln Yt}进行拟合ARIMA模型,根据与准则,得到最优模型ARIMA(0,0,1)。
2.2 筛选影响因子
利用多元线性回归分析,对影响因子进行筛选,找出影响人均GDP与GDP增长率的主要因素,以便下一步进行预测。首先选取了传统方法中常用的7个影响因子,分别标记为X1~X7,具体如表1所示。
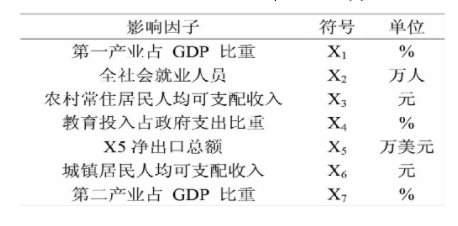
表1 经济发展影响因子
为分析表1中的影响因子对人均GDP与GDP增长率的影响,建立多元线性回归方程。
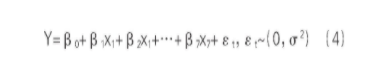
式中,Y表示:被解释变量,即某区域GDP;xi表示:解释变量,即表2中的7个影响因子;β0β1…β7表示:回归系数;σ表示:未知参数。
使用R语言对多元线性回归方程逐步回归计算,基于AIC准则,剔除AIC使函数值减小至最低的变量。
剔除的变量为X2、X3、X4、X7,表中三个变量的显著性分别为'***'0.001显著、'***'0.001显著、'**'0.01显著,概率都小于5%,故认定X1、X5、X6这三个指标与之间有着明显的线性关系,可以用来进行有效预测。
2.3 输入指标
在预测前对原始数据进归一化处理:
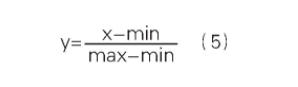
反归一化处理为:
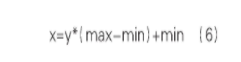
式中,x表示:原始数据,max、min分别表示x的最大值、最小值,y表示处理后的数据。利用R语言进行拟合模型,语句为:met Ts(data,m3,size),输入变量X1、X5、X6,经反归一化处理完成预测。
3. 模拟预测
3.1 模拟准备
本次研究中,选取平均绝对百分比误差(MAPE)对三种预测方法的结果进行分析。
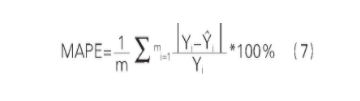
式中,Yi表示:真实值;Y赞i表示:预测值;m表示:预测点数。MAPE能够不受纲量影响,可以稳定地反应出预测值与真实值的误差水平,当MAPE值小于10%时,预测结果为高精度;当MAPE值在10%到20%之间时,预测结果为良好;当MAPE值在20%到30%之间时,预测结果为可行:当MAPE值高于30%时,预测结果为错误。
3.2 人均GDP模拟预测结果与分析
将三种方案进行模拟预测的结果与真实值进行对比,如图1所示,计算平均绝对误差百分比(MAPE),得到的数据如表2所示。
图1 三种方案人均GDP模拟预测结果对比
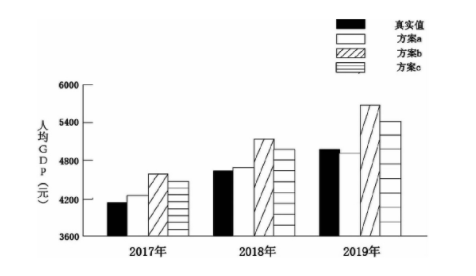
由图1可知,2017年、2018年、2019年方案a的人均GDP模拟预测结果与真实值最为接近,方案b的人均GDP模拟预测结果与真实值相差最大。
由表2可知,2017年方案a人均GDP模拟预测结果的MAPE值为1.36%,比方案b和方案c分别低了1.47%、0.98%;2018年方案a人均GDP模拟预测结果的MAPE值为0.85%,比方案b和方案c分别低了4.72%、3.37%;2019年方案a人均GDP模拟预测结果的MAPE值为2.17%,比方案b和方案c分别低了5.68%、3.17%.
3.3 GDP增长率模拟预测结果及分析
将三种方案进行模拟预测的结果与真实值进行对比,计算平均绝对误差百分比(),得到的数据2017年、2018年、2019年方案a的GDP增长率模拟预测结果与真实值最为接近,方案b的人均GDP模拟预测结果与真实值相差最大。
表2三种方案人均GDP模拟预测MAPE比较
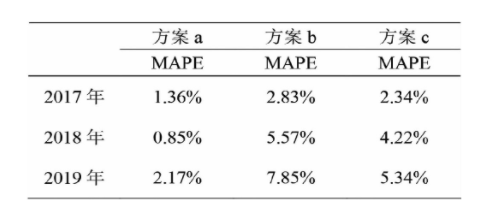
表3三种方案GDP增长率模拟预测MAPE比较
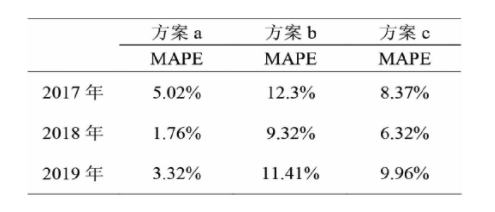
由表3可知,2017年方案a GDP增长率模拟预测结果的MAPE值为5.02%,比方案b和方案c分别低了7.28%、3.35%;2018年方案a GDP增长率模拟预测结果的MAPE值为1.76%,比方案b和方案c分别低了7.56%、4.56%;2019年方案a GDP增长率模拟预测结果的MAPE值为3.32%,比方案b和方案c分别低了8.09%、6.64%.
4. 结束语
本文通过多元统计分析方法的应用,提高了区域经济发展预测的准确度,为经营主体制定政策与规划未来发展提供了有力的数据支持。今后将对区域经济发展中的预测进行深入研究,以期在其他方面为经济发展做出更多贡献。
参考文献
[1]张艳丽基于多元统计分析的区域经济绿色发展水平预测及优化路径探讨[J]统计与管理,2020,35(11):36-43.
[2]王若蕾基于多元统计分析地区私营企业和个体就业人数研究[J].现代营销(下旬刊),2020(07):193- 195.





