摘 要: 针对不同形式的退火炉,利用计算的通用性,开发出一套适用于立式或卧式的连退炉、镀锌炉等数学模型,继而开发一套控制系统,包括带钢温度跟踪、操作参数设定、换带策略制定等功能。通过现场验证,证明了模型的可靠性和准确性。
关键词 : 退火炉;数学模型;控制系统;换带策略;
Abstract: Because of the universality of calculation, build a set of mathematical models which suitable for vertical or horizontal continuous annealing furnace or galvanizing furnace, and then developed a set of control system, including strip temperature tracking, operation parameter setting, strip change strategy formulation and other functions. The reliability and accuracy of the model are proved by field verification.
Keyword: annealing furnace; mathematical model; control system; changing strategy;
连续退火炉是汽车板、家电板等生产线上重要的生产设备之一,其功能是根据设定的带温曲线,对表面清洁过的冷却带钢逐次进行不同的热处理,最终出炉打卷成为标准产品。根据形式不同,连续退火炉可分为立式和卧式两种;根据工艺又可分为连退、镀锌、镀铝等退火炉。区别在于设置明火加热段、过时效段等,对应的热处理工艺不同。但是从数学模型角度,计算方法、原理相同,只是在处理边界热流时选择不同的计算方法,因此建立一套通用的数学模型可以适应不同的退火炉型。
连续退火炉模型系统是从带钢单元入炉开始建立带钢热跟踪,直到带钢出炉结束为止。其控制方法是在保证带钢各段目标出口温度的前提下,通过对各控制段的炉温、辐射管温度、风机功率等参数进行设定,最终满足各种材料的热处理目标温度。
1 、数学模型研究
1.1 、跟踪模型
通过建立热平衡,计算带钢与控制段之间的温度关系,迭代求出平衡下的计算值。控制方程为:
q=cm(Tout?Tin)q=hA(Tf?Tmid)+?σA(T4f?T4mid)Tmid=(Tout+Tin)/2(1)
式中:Tout为带钢行程出口温度,K;Tin为带钢行程进口温度,K;Tmid为带钢行程平均温度,K;Tf为辐射管温或者炉温,K;h为对流换热系数,W/ (m2·K);c为带钢比热,J/(kg·K);m为带钢质量,kg; A为传热面积,m2;q为边界热流量,W。
通过数学迭代的计算方法,根据已知的带钢温度Tin求出该行程的Tout,并将Tout作为下一行程的Tin,循环计算直到算完全部节点为止,将所有计算值连接起来即为带钢在加热段的温度分布曲线。
1.2、 边界热流
1.2.1 、喷射换热
喷射换热适应于立式或者卧式退火炉的预热段、快冷段和缓冷段。冲击射流是射流对固体表面的冲击流动,即气体或液体在压差的作用下,通过圆形或窄缝形喷嘴垂直(或成一定倾角)喷射到被冷却或加热表面上。喷流加热、冷却是依靠冲击射流强化流体与固体表面的换热。

带钢在喷流装置中的换热系数与喷流装置的结构形式、喷流口的尺寸、喷箱与带钢的距离、喷气压力、喷流介质的物性等因素有关。对于这种复杂的换热方式,目前没有精确的数学分析解,只能采用根据实验拟合得到的经验公式进行研究。
据有关文献研究表明[1],Holger Martin所得的计算公式较为准确,应用范围较广。
(1)对于圆形喷嘴的喷箱,Holger Martin拟合的公式为:
NuPr0.42=f√?Re23?[1+(H/D0.6/f√)6]?0.05?1?2.2f√1+0.2(H/D?6)f√(2)
式(2)的适用范围:2000≤Re≤105;0.004≤f≤0.04;2≤H/D≤12。
(2)对于平行狭缝喷嘴的喷箱, Holger Martin拟合的公式为:
NuPr0.42=23f3/40(2Re?f?f0f2+f20)2/3 (3)
式(3)的适用范围:1500≤Re≤4×104;0.008≤f≤2.5f0(H/D);1≤H/D≤40。
式中:H为喷孔与带钢表面的垂直距离,m; D为喷孔直径,m; f为相对喷孔面积。对于圆形喷孔,三角孔阵,f=π23√(DLD)2;对于平行狭缝喷嘴组,f=BLT,f0(HS)=[60+4(HS?2)2]?1/2。
当射流中心线与喷射表面的夹角φ不小于60°时,H由H′代替:H′=H/sinφ。
如果喷孔外带有收缩形的短喷嘴,需要将喷出速度,喷孔直径,相对喷孔面积等由以下相应值代替:W′=W/ε,D′=D/ε1/2,f′=f·ε,其中,ε为喷孔面积收缩系数。
转化成热流密度的表达式为:
q=hΔt=λNuxΔt (4)
式中:q为带钢表面的热流密度,W/m2;h为带钢与炉内气流的对流换热系数,W/(m2·K);λ为炉内气体的导热系数,W/(m ·K);Δt为带钢与气体之间的温差, K。
1.2.2 、明火加热
明火加热适应于卧式退火炉的加热段。在明火加热炉中,钢带表面和炉气之间有辐射和对流传热,但对流传热比例很小,一般不予考虑。因此,可以采用导来辐射系数法计算带钢表面热流密度。
简化明火炉膛内部辐射换热,钢带表面的热流密度qu为:
qu=kuCgwm[(Tf100)4?(Ts100)4]+α(Tf?Ts)(5)
式中:ku为带钢表面热流修正系数;Tf为炉膛炉气温度,K;Ts为带钢表面温度,K;α为炉气和带钢表面之间的对流传热系数,W/(m2·K);Cgwm为导来辐射系数,W/(m2·K4)。
在炉气均匀地充满炉膛,炉壁的差额热流等于零的条件下,导来辐射系数的计算公式为:
Cgwm=5.67εgεm[1+ΦCH(1?εg)]εg+ΦCH(1?εg)(εg+εm?εgεm) (6)
式中:εm为钢带表面黑度,计算时取常数εm=0.2~0.3;εg为炉气黑度;ΦCH为炉壁对钢带表面的角系数。
ΦCH按如下公式计算:
ΦCH=W2(H+B)?W (7)
式中:W为钢带宽度,m ;H为炉膛高度,m; B为炉膛宽度,m。
炉气黑度εg按如下经验公式计算:
εg=εCO2+1.05εH2O (8)
εCO2=0.71×(PCO2S)1/3/(Tg/100)?0.5 (9)
εH2O=7.1×P0.8H2O×S0.6/(Tg/100)?1 (10)
式中:εCO2为CO2的黑度;εH2O为H2O的黑度;PCO2为CO2的分压,大气压;PH2O为H2O的分压,大气压;S为平均射线行程,m; Tg为炉气温度,K。
平均射线行程S按如下经验公式计算:
S=3.6HB2(H+B) (11)
式中:H为炉膛高度,m; B为炉膛宽度,m。
1.2.3、 辐射管加热
辐射管加热适应于立式或者卧式退火炉的辐射管加热段、均热段和立式退火炉的过时效段。
在辐射管加热段和均热段,传热方式主要以辐射为主,炉子气氛主要是还原性气体,氮气和氢气为双原子分子,无辐射能力,因此在加热段内,主要是辐射管对带钢的辐射,炉墙对带钢的辐射和带钢之间的辐射影响很小。
任意控制区域是由带钢(炉墙)、辐射管、带钢(炉墙)三个组成封闭系统计算内部辐射换热,首先将三个元素视为等温灰面,建立每个表面的有效辐射热流方程式,则有如下方程组:
计算模型可简化为矩阵:
AX=B (13)
A=???(1+φ1.1(ε1?1))(ε2?1)φ2.1(ε3?1)φ3.1(ε1?1)φ1.2(1+φ2.2(ε2?1))(ε3?1)φ3.2(ε1?1)φ1.3(ε2?1)φ2.3(1+φ3.3(ε3?1))???,B=????ε1σ0T41ε2σ0T42ε3σ0T43????
式中:J为有效辐射,W/m2;φ为辐射角系数;ε为黑度;T为温度,K。
根据温度、有效辐射量求出各个表面的净辐射热流密度,建立方程组:
CX=D (15)
C=???(φ1.1?1)φ2.1φ3.1φ1.2(φ2.2?1)φ3.2φ1.3φ2.3(φ3.3?1)???
式中:D为各个表面的辐射热流密度。在求解方程组时,需要运用以下公式计算:通过式(13)计算出X=A?1B=A?B|A|,再通过式(15)计算出D=CX=CA?B|A|。
1.3、 换带策略模型
带钢的过渡过程是指两种不同规格(厚度和宽度)、不同热处理温度带钢焊接在一起,在退火炉里进行热处理的过程,即换带过程。
以薄变厚为例(类推厚变薄):一般带钢由薄变厚,在相同条件下,即吸收的热量在不变的情况,根据公式q=cmΔt,温差与厚度成反比,因此焊缝后的带钢出口温度会下降,此时需要根据厚带钢下降的温度值与目标值之间的关系来确定换带策略。
1.3.1、 目标温度范围有重叠区的换带策略
以加热段为例,由图1可知,带钢1和带钢2的目标温度区间相同,此时的策略是将带钢出口温度从带钢1的上限值过渡到带钢2的下限值,即将带钢1升温至上限值,然后因为厚度增加,厚带钢出口温度降低,要求降低到的最小值为带钢2的下限值;最后再缓慢升温至带钢2的目标温度值。此时带钢在换带前后均满足热处理温度要求。
图1 薄变厚换带策略一
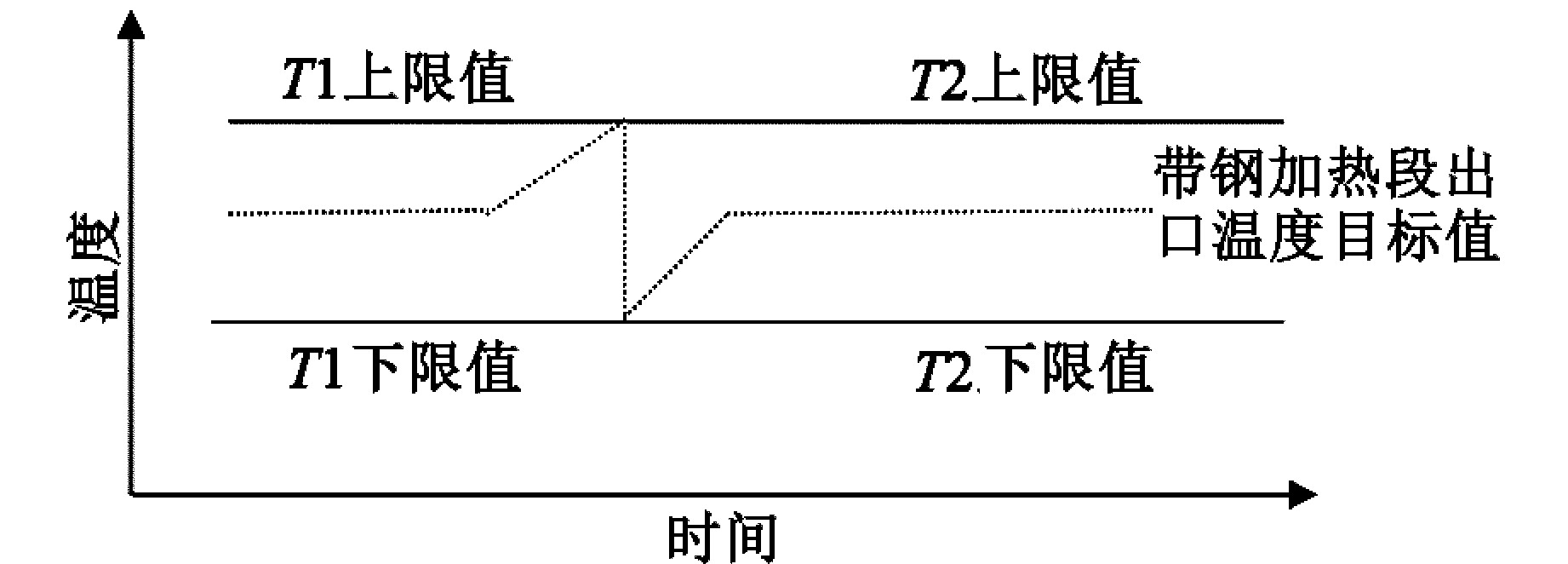
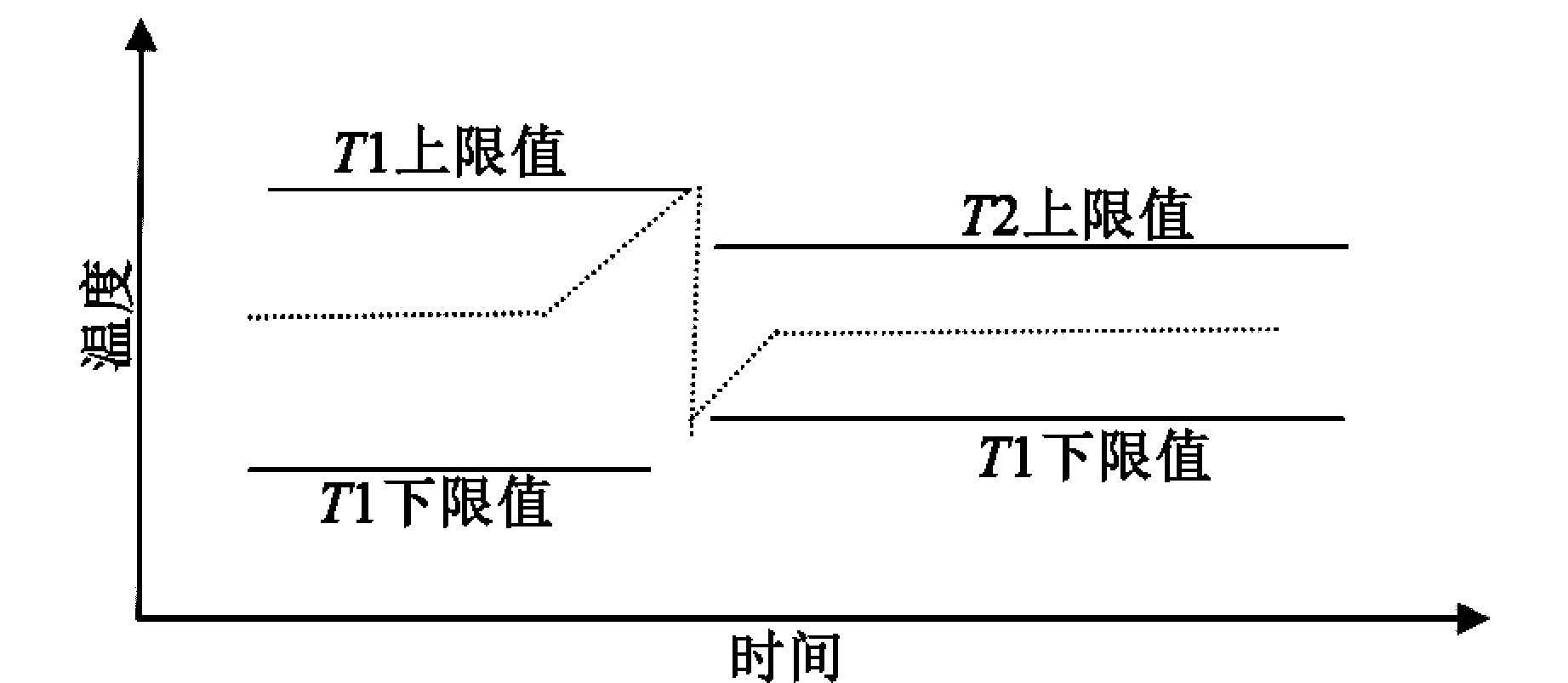
以加热段为例,从图2可知,带钢2的目标温度区间高于带钢1的目标温度区间,但有重叠区间,此时的策略是将带钢出口温度从带钢1的上限值过渡到带钢2的下限值,同理此时带钢在换带前后均满足热处理温度要求,薄变厚换带策略二对带钢焊缝前后允许变化的温差较小。
图2 薄变厚换带策略二
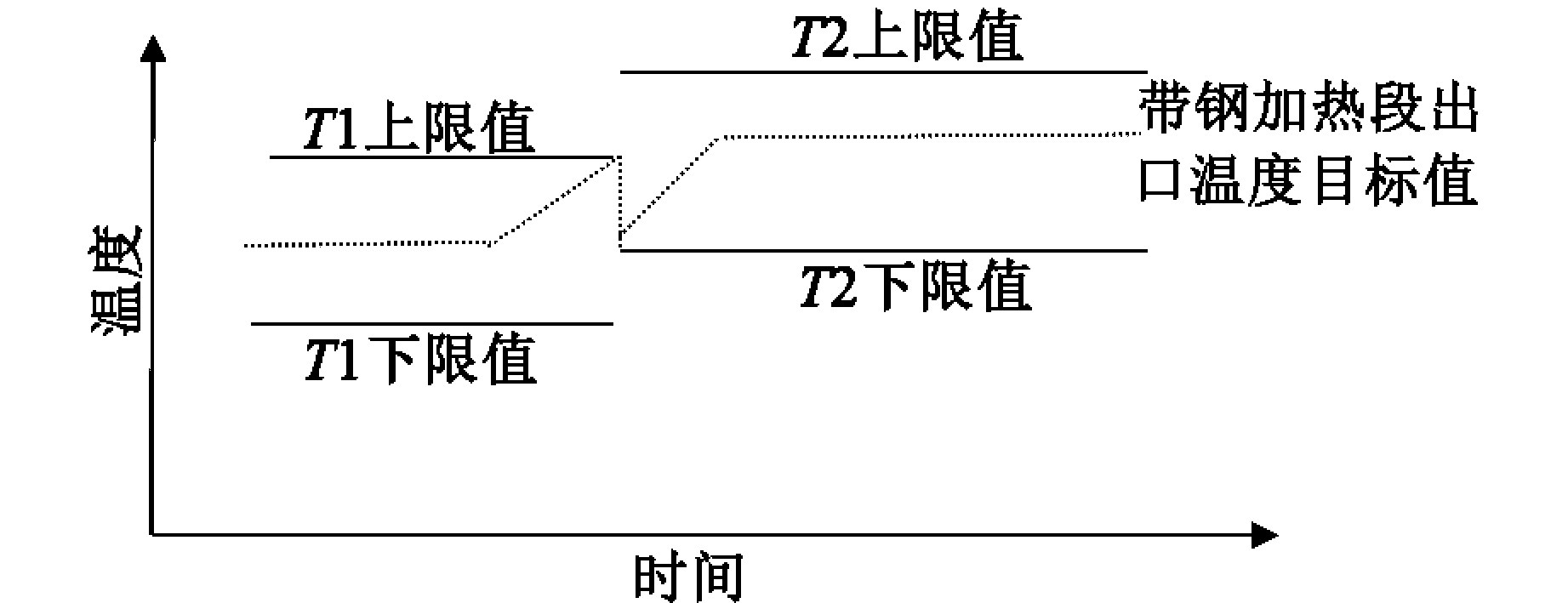
从图3可知,带钢2的目标温度区间低于带钢1的目标温度区间,但有重叠区间,此时的策略是将带钢出口温度从带钢1的上限值过渡到带钢2的下限值,同理此时带钢在换带时前后均满足热处理温度要求。由图可见,对带钢允许的温差较大,因此该策略适用于带钢厚度差特别大的情况。
图3 薄变厚换带策略三
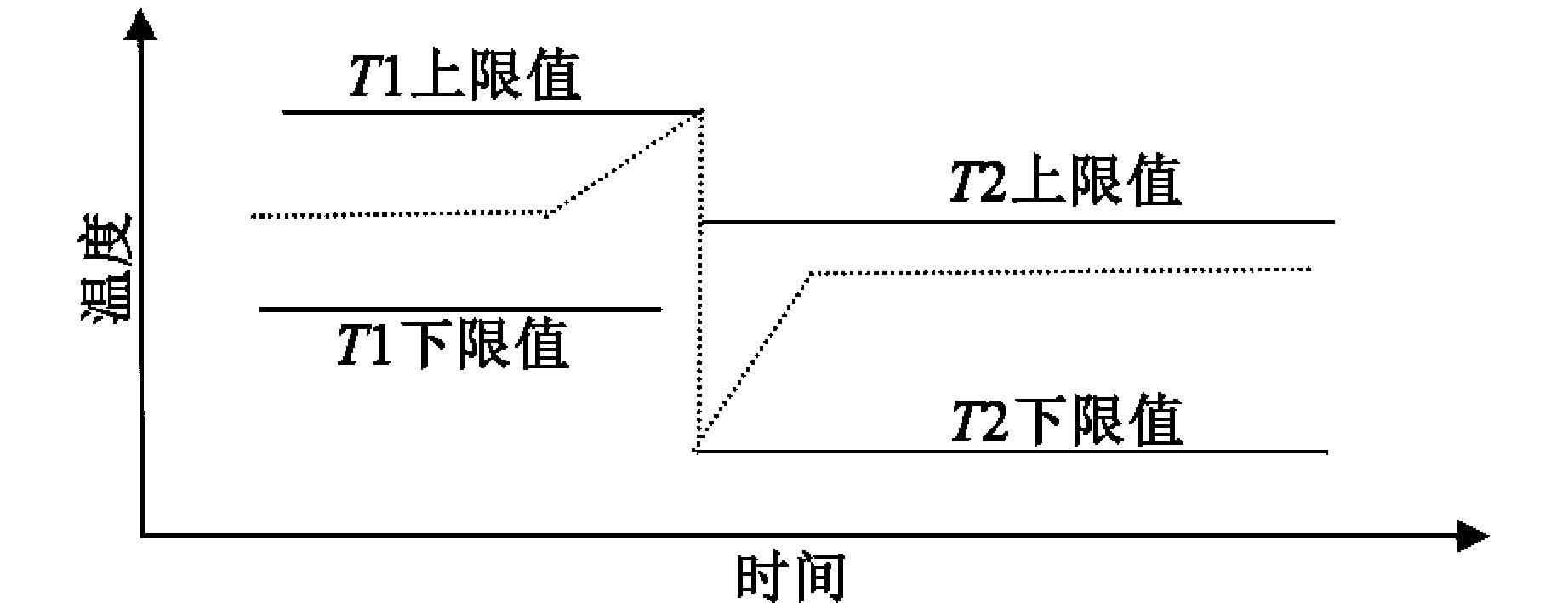
从图4,5可知,此时临界控制范围为带钢1的从上限值过渡到带钢2的下限值,此情况同策略1相似,计算方法相同
图4 薄变厚换带策略四
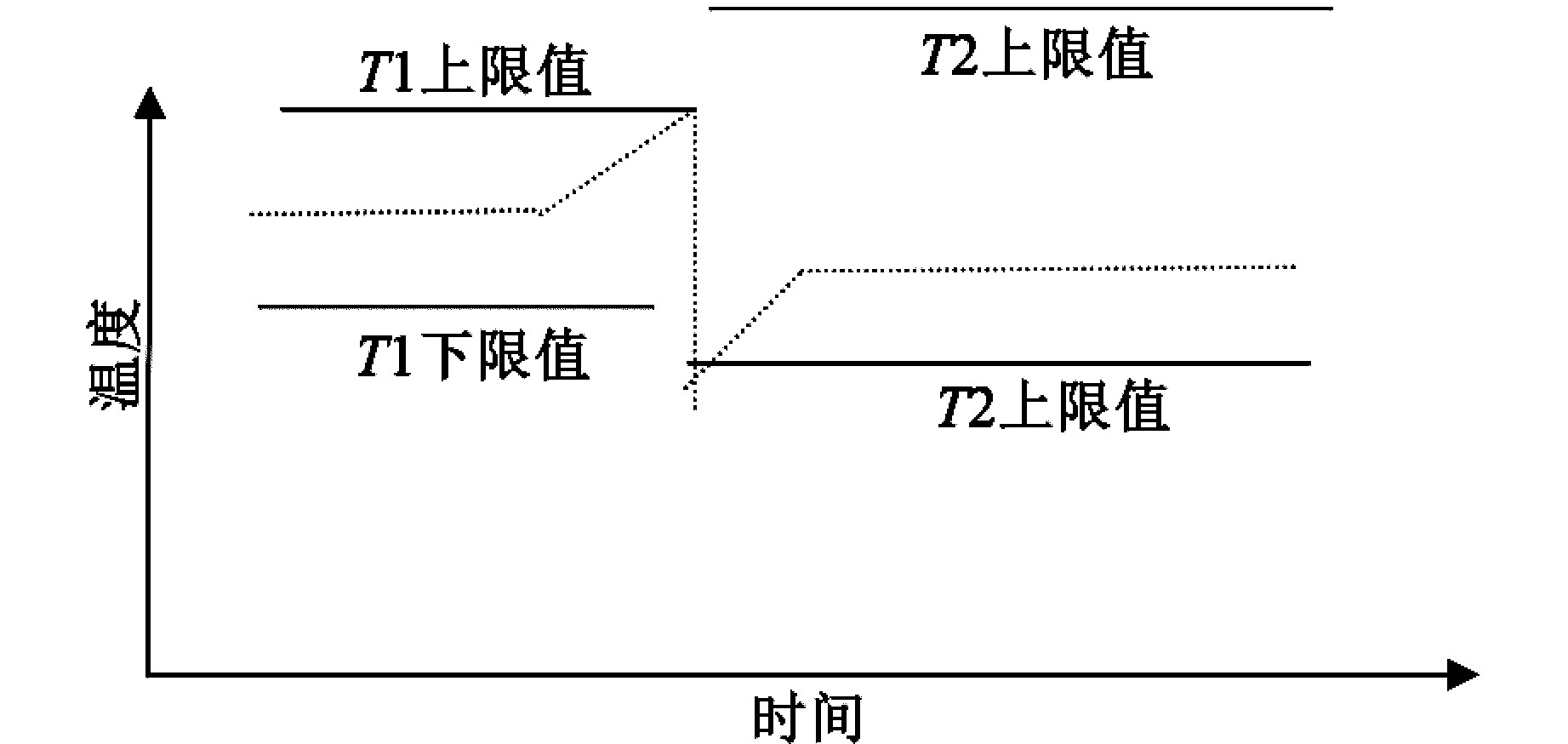
图5 薄变厚换带策略五
1.3.2 、目标温度范围无重叠区的换带策略
图6带钢2的目标温度区间高于带钢1的目标温度区间,无重叠区间,此情况因为目标温度与带温变化趋势相反,因带钢2的热处理温度更高,此时的策略将带钢1的出口温度升温至某一值,然后因为厚度变大,厚带钢温度降低,要求降低到带钢2的下限值,即以带钢2的下限值为控制目标,此时带钢在换带后满足带钢2的生产要求。此情况需要牺牲一部分带钢1的产量,设置过渡卷。
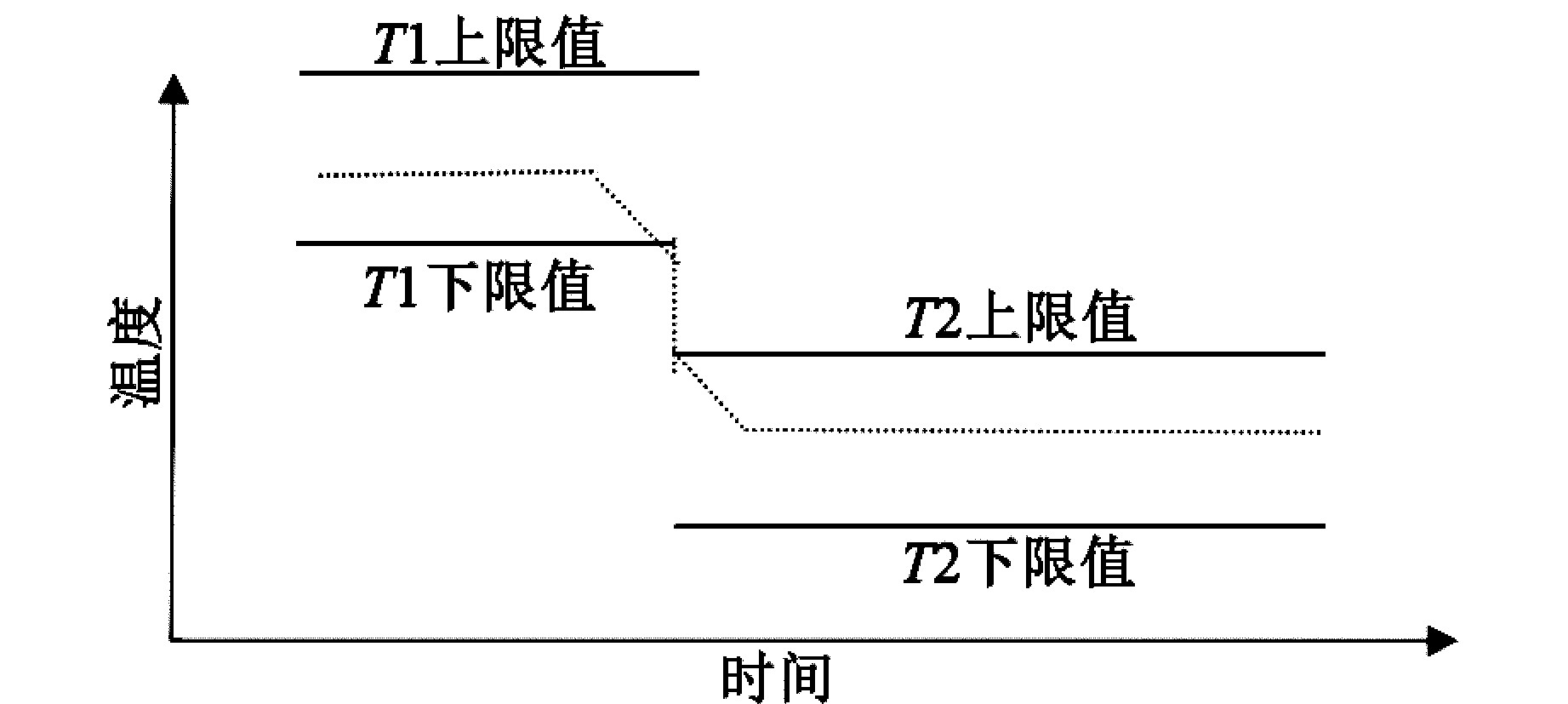
图7中,带钢2的目标温度区间低于带钢1的目标温度区间,无重叠区间,此情况因为目标温度与带温变化趋势相同,可不改变参数或改变较小参数实现快速过渡。
通过上述分析,总结具体计算流程:
图6 薄变厚换带策略六
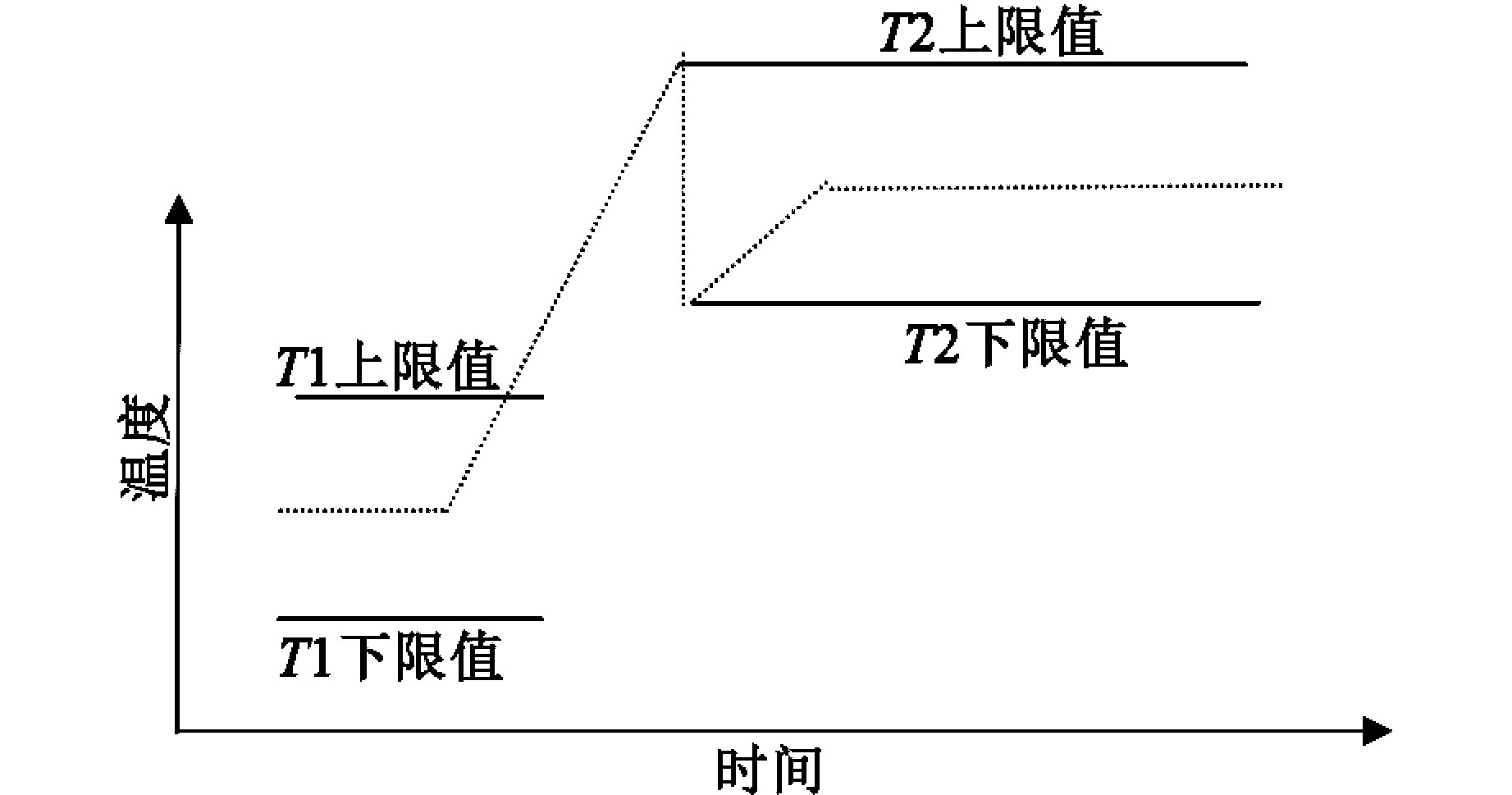
图7 薄变厚换带策略七
(1)根据当前退火炉带钢运行速度,通过数学模型,计算两种规格在目标温度下的辐射管温度设定值作为过渡前后带钢1和带钢2的运行速度和温度设定值。
(2)根据换带类型,判断前后带钢目标温度是否有重叠区域,有重叠部分,则根据薄变厚,选择前一带钢温度的上限值,或者根据厚变薄选择前一带钢温度的下限值作为目标温度,计算前一带钢在该温度下的辐射管温度设定值作为过渡期间的温度初始设定值。
(3)计算在该辐射管温度,带钢运行速度为当前运行速度下带钢2的出口温度,若出口温度在允许范围内,则当前辐射管设定值为过渡期间的辐射管设定值,若不在允许范围内,则通过调整辐射管目标温度的方法使其在允许范围内,具体为:①出口温度低于下限值,则减小速度,重新计算辐射管温度设定值,再计算后一带钢出口温度,若仍低于下限值,则继续减小,若高于下限值,则当前的速度和辐射管温度即为第二阶段的速度和温度设定值。②出口温度高于上限值,则降低前一带钢的上限目标值,重新计算辐射管温度设定值,再计算后一带钢出口温度,若仍高于下限值,则继续减小,若低于下限值,则当前的速度和辐射管温度即为第二阶段的速度和温度设定值。
2 、控制系统开发
2.1、 系统一般构成
退火炉控制系统的典型构成包括一台PC服务器(置于电气室)、一台工程师站(置于电气室)、一台操作终端(置于中央操作室)和一台交换机(置于电气室)组成。PC服务器作为退火炉模型系统主机,主要完成退火炉内带钢焊缝跟踪、自动温度控制计算、数据处理及数据通讯等功能。操作终端主要用于显示退火炉内带钢焊缝的跟踪情况,以及温度设定的选择和修正。工程师站主要用于对退火炉模型系统的开发和维护。
2.2 、应用功能
退火炉控制系统包括应用和模型两个部分,其中应用部分是针对退火炉进行数据采集、通讯等管理操作。比如:数据采集以及下发,包括带钢生产数据处理、焊缝位置、带钢速度、各段出口带温、退火炉工况参数、班管理、报表打印等。
2.3 、模型功能
退火炉模型作用是在生产规格(带钢厚度,速度等)、生产等级(材料的退火温度)和退火炉能力(辐射管的加热能力等)等条件一定的情况下,使带钢经过在退火炉内的运行后满足工艺温度条件,同时使带钢内部组织性能满足产品要求,并且经过退火后产品性能良好;此外还要根据生产状况来优化带钢的退火过程。
启动模型后开始实时检测数据,定时启动相关计算,其中稳态设定值以及换带策略计算完成保存在数据库中,方便程序直接调用。
模型首先判断是否为新规格,判断新规格条件为设定值数据库是否存在该规格的材质、厚度或者宽度,如果是,则直接调用设定计算模块,保存设定值在数据库初始设定值表格内。并将设定值标记为新的设定值,下达参数,结束本周期计算,待进入下一周期。
若模型判断非新规格,则下一步判断是否为规格变化,规格变化条件是前后带钢的材质、厚度和宽度不一致,若发生变化,则调用或者计算换带策略,并标记启动换带策略。下一步是判断是否启动换带,启动换带条件是启动换带标志为是以及焊缝位置达到第一个设定点,启动换带后,根据焊缝位置到达设定点的位置,下达对应得设定值,直接结束本周期计算。
若模型非启动换带,一般为正常的稳态控制,则根据检测的设定值,计算带钢预估的出口温度,计算后则判断是否进行修正反馈计算,根据带钢温度反馈,计算出新的修正系数以及新的设定值。最后输出设定值以及带钢出口温度,进入下一周期计算。
主要包含计算模块为:新规格计算模块、带钢预测温度计算模块、换带策略计算模块、带钢温度修正计算模块、自学习计算模块。
3 、在线实施
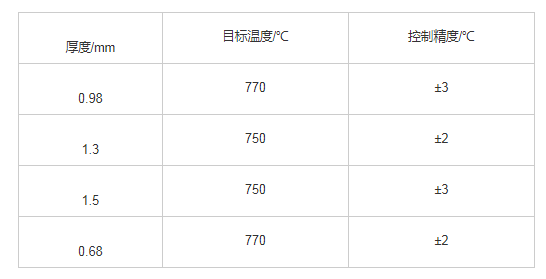
某镀锌线在生产达到稳态(即炉内温度偏差±20 ℃内)后,该模型投入使用,共参与控制产品厚度包括0.68、0.99、1.14、1.3、1.4、1.5、2.0 mm共7种规格,带钢加热段出口温度与目标值的偏差见表1。
表1 带钢加热段出口温度与目标值偏差
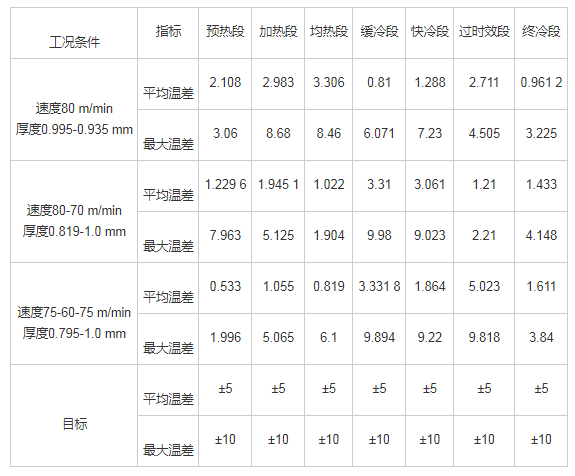
该模型应用于某连退线,其换带过程中各段出口温度与目标温度的偏差值,基本满足指标要求,具体数据如表2所示。
表2 连退线各段出口温度与目标值偏差
4 、结论
设计开发连续退火炉带钢数学模型,通过工程实践验证模型的可靠性和准确性,对研究带钢在线控制有很好的借鉴意义。在后续的研究中会针对极薄带钢的控制和对张力、热变形等加强研究,提升对更多规格和生产状况的适用性。
参考文献
1杨进带钢连续热镀锌锌沮火炉技术及卧式连续退火炉敬学模型研究D|北京科技大学,2002.





