第 4 章 服装设计师品牌微博营销参与意愿实证分析
本章运用 SPSS 统计软件对收集的有效问卷进行相关分析。首先对第一部分和第二部分进行描述性统计分析,然后对主问卷的量表进行信度和效度检验,在问卷质量达标的前提下,再对服装设计师品牌微博营销参与意愿的影响因素进行相关性分析,最后对其进行回归分析,并得出消费者微博营销参与意愿的量化方程式。
4.1 样本描述性统计分析
本节分为两部分,第一部分受访者基本信息分析。第二部分微博用户使用行为分析。
4.1.1 样本基本信息分析4.1.1.1 样本性别分布【1】
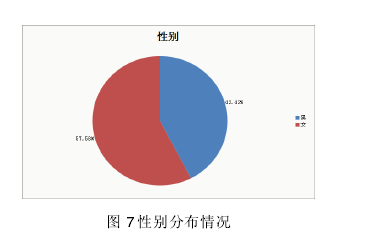
从图 7 可以看出,本研究样本的女性微博用户占比是 57.58%,男性微博用户占比42.42%,女性用户人数略高于男性用户人数,男女比例为 1:1.35,相对均衡,具有较好代表性《。2013年微博用户发展报告》数据显示,国内微博核心用户中女性用户的占比 57.40%,这表明本样本的性别分布与相关报告一致,调查具有较高的可信度。
4.1.1.2 样本学历分布【2】
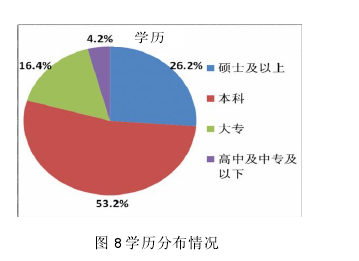
从图 8 数据中可以看出,本研究样本中本科占比居首,达到了 53.2%;硕士及以上占比次之,达到了 26.2%;大专学历样本占比是 16.4%;高中及以下占比最少,为 4.2%。《2013年微博用户发展报告》数据显示,微博用户以高学历人群为主,其中大专及以上学历的用户占 70%,这表明本样本的学历分布与相关报告一致,调查具有较高的可信度。
4.1.1.3 样本职业分布【3】
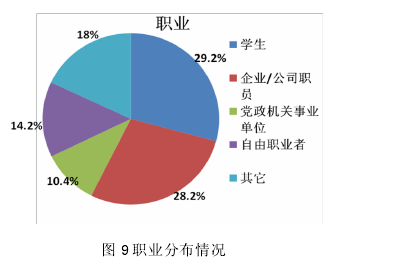
从图 9 中可以看出,本研究样本的学生占比为 29.2%,企业/公司职员占比为 28.2%,两者加和占比为 57.4%。《2013 年微博用户发展报告》数据显示,微博用户以学生与公司员工为主,这表明本样本的职业分布与相关报告一致,调查具有较高的可信度。
4.1.2 样本使用微博基本情况4.1.2.1 样本使用的微博品牌【4】
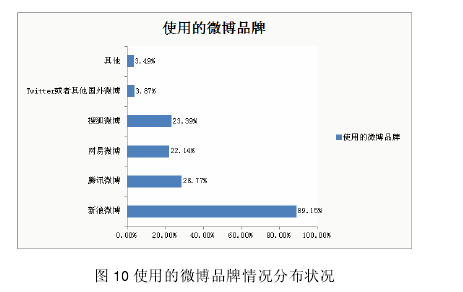
由图 10 分析中可以看出,新浪微博占样本用户使用微博品牌的 89.15%,其次是腾讯微博和网易微博,分别为 28.77%和 22.14%。由此可以看出,服装设计师品牌进行微博营销的主战场是新浪微博,上面汇聚的关注者最多。4.1.2.2 样本使用微博的历史【5】
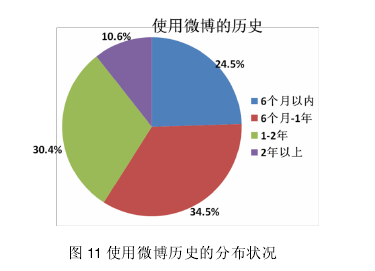
从图 11 数据可以看出,本研究样本的消费者关注微博 6 个月-1 年的人数最多,占34.5%,1-2 年的次之,占 30.4%。
4.1.2.3 样本平均每天登陆微博频率【6】
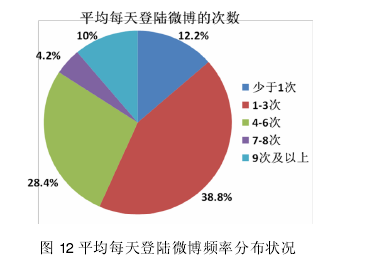
从图 12 中数据可以看出,占总样本 38.8%的消费者每天登陆微博 1-3 次,占总样本28.4%的消费者每天登陆微博 4-6 次。
4.1.2.4 样本平均每天使用微博的时间【7】
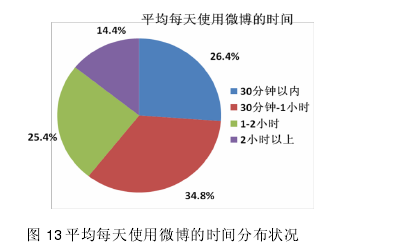
从图 13 中数据可以看出,本样本占比 34.8%的消费者每天花费 30 分钟-1 小时关注微博,占比 26.4%的消费者用 30 分钟之内的时间关注微博,占比 25.4%的消费者会花费 1-2小时关注微博,这说明微博已经成为样本受访者经常使用的社交媒体之一。
4.1.2.5 样本关注服装设计师品牌微博【8】
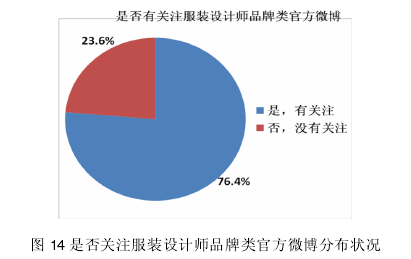
从图 14 数据可以看出,样本消费者中有 76.4%关注了服装设计师品牌微博,说明服装设计师品牌微博在样本调查者中还是普遍具有较高关注度的。在此题中没有关注服装设计师品牌微博的受访者,则停止作答;关注服装设计师品牌微博的受访者继续完成剩余问卷。
4.2 量表的信度和效度检验
4.2.1 信度检验为有效反映本数据的一致性、稳定性以及可靠性程度,在对问卷进行其他数据分析前,先进行信度检验。本研究借助 SPSS17.0 软件对样本进行信度分析,自变量和因变量的Cronbach's a 系数值见表 13。【9】
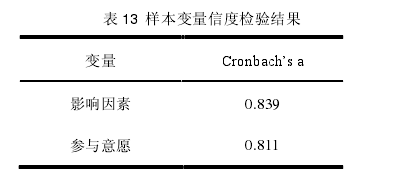
本文依据 Cronbach's a 信度标准对问卷信度进行测量(见上文表 10),从表 13 可知,服装设计师品牌微博营销影响因素的信度系数为 0.839 大于 0.7,参与意愿的信度系数为0.811 也大于 0.7,这说明样本问卷的可信度很高。4.2.2 效度检验本研究釆用 KMO 检验和 Bartlett's 球形检验方法,来进行调研问卷的变量效度检验。
KMO 测查变量间的偏相关性,如果 KMO 值小于 0.5 认为样本不合适进行因子分析。
Bartlett's 球形检验考虑的是整个相关矩阵,如果指标达到显着性水平(即 sig.值小于 0.05)则说明母群体的相关矩阵间有共同因素存在,可以做因子分析。笔者对服装设计师品牌微博营销影响因素和参与意愿这两类都进行 KMO 检验和 Bartlett's 球形,结果如表 14 所示。【10】
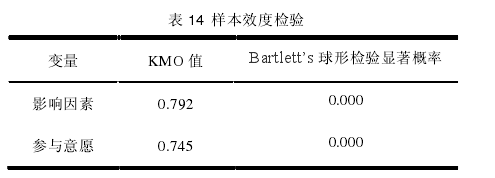
由上表可知,本样本问卷影响因素和参与意愿的 KMO 值均高于 0.7,且 Bartlett's 球形检验皆达到显着水平,所以适合进行因子分析。
4.3 因子分析
因子分析是指研究从变量群中提取共性因子的统计技术。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
本研究采用主成分分析法,对服装设计师品牌微博营销影响因素和参与意愿分别进行主成分分析,提取出具有代表性的因子。学者研究认为因子载荷值越大,变量测量到的共同因素特质越多。在选择测量项目时,因子载荷值大小可以作为保留和删除该项目的标准。
本研究主成分分析法提取显着性因子的标准为:因子所包含的各变量项因子载荷值大于0.5,主成分的累计贡献率大于 40%。本研究变量是基于以往学者的研究论证和实际经验而构造的模型,因此依据事先决定准则确定因子个数。
4.3.1 服装设计师品牌微博营销影响因素的因子分析对有效样本的服装设计师品牌微博营销影响因素进行主成分分析,本文变量是基于以往学者研究论证,因此依据事先决定准则确定公因子数量是 6,这 6 个因子反映的有用变量信息是 76.325%,表 15 为解释的总体方差结果。本文采用方差极大法进行因子旋转,结果见表 16。本研究提取因子的标准定为因子载荷值得绝对值大于 0.5。 根据表可知:
(1)第一主成分中,“我认为关注服装设计师品牌微博,有利于降低品牌信息的搜索成本”“我认为关注服装设计师品牌微博,有利于掌握品牌的最新信息”“我认为关注服装设计师品牌微博,有利于提高品牌服饰的购买效率”这三项因子载荷值都大于 0.7,因此这三个问题可以反映“感知有用性”这一因子对服装设计师品牌微博营销的影响。
(2) 第二主成分中,“服装设计师品牌知名度越高,越容易引起我的关注”“服装设计师品牌美誉度越高,越容易引起我的关注”“服装设计师品牌个性越鲜明,越容易引起我的关注”这三项因子载荷值都大于 0.7,因此这三个问题可以反映“品牌因素”这一因子对服装设计师品牌微博营销的影响。
(3) 第三主成分中,“我认为服装设计师品牌发布的微博信息是真实可靠的”“我可以从服装设计师品牌发布的微博中了解专业性讯息”“我认为服装设计师品牌是利用微博第一时间发布信息的”“我认为服装设计师品牌发布的微博信息趣味性”这四项因子载荷值都大于 0.6,因此这四个问题可以反映“微博信息质量”这一因子对服装设计师品牌微博营销的影响。
(4) 第四主成分中,“我认为通过微博,服装设计师品牌可以加深同客户的沟通”“我认为通过微博,我可以加深和朋友们的沟通”这两项因子载荷值都大于 0.6,因此这两个问题可以反映“微博互动性”这一因子对服装设计师品牌微博营销的影响。
(5) 第五主成分中,“我身边的大多数朋友都有使用微博”“我身边的大多数朋友都认为品牌通过微博进行营销是有效果的”这两项因子载荷值都大于 0.6,因此这两个问题可以反映“社会影响”这一因子对服装设计师品牌微博营销的影响。
(6)第六主成分中,“我认为搜索、关注我喜欢的服装设计师品牌微博很容易”“我认为分享(转发、评论)服装设计师品牌微博很容易”这两项因子载荷值都大于 0.5,因此这两个问题可以反映“感知易用性”这一因子对服装设计师品牌微博营销的影响。
“我认为关注服装设计师品牌微博,有利于增进我对朋友的了解”“其他途径也会引导我关注服装设计师品牌微博”没有进入主成分,因此舍弃这两个测量项目。
4.3.2 参与意愿因子分析对有效样本进行参与意愿变量的主成分分析,如表 17。【11】
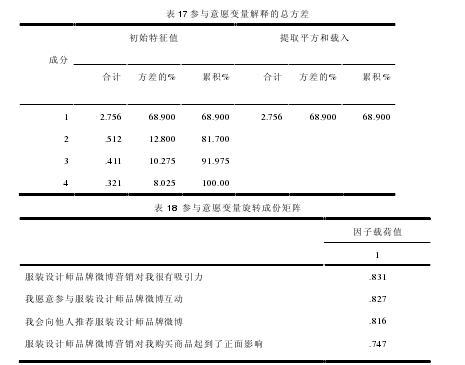
从表 17 可以看出,特征根的因字数是 1,该因子的累计贡献率是 68.900%。表 18 可以看出,参与意愿测量项目因子载荷值都大于 0.7,说明这四个问题都是“参与意愿”因变量的测量问题。
4.3.3 因子分析小结服装设计师品牌微博营销影响因素有 6 个变量: 感知有用性、感知易用性、社会影响、微博信息质量、微博互动性、品牌因素;参与意愿的四个测量项目也通过验证。
4.4 相关分析
两个变量之间是否有某种依存关系,用相关系数表示两者之间相关方向及程度。本文采用 Pearson 分析方法研究感知有用性、感知易用性、社会影响、微博信息质量、微博互动性和品牌因素同消费者服装设计师品牌微博参与意愿之间的相关关系。相关系数大于0.9,表明两个变量之间存在显着性相关;相关系数大于 0.8,说明两个变量之间存在高度相关;相关系数小于 0.8 且大于 0.5,说明两者之间中度相关;相关系数小于 0.5 且大于 0.3,说明两个变量存在低度相关;相关系数小于 0.3,说明两个变量极弱相关。本文将六个服装设计师品牌微博影响因素参与意愿变量进行相关分析,结果如表 19。【12】
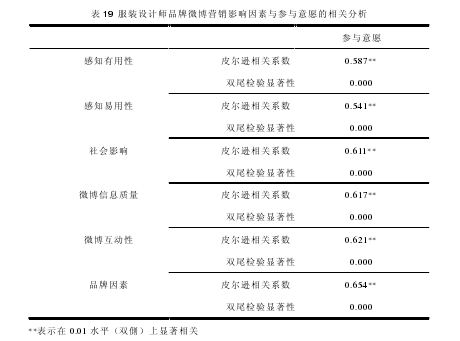
从表 19 可知,服装设计师品牌微博营销的影响因素中的感知有用性、感知易用性、社会影响、微博信息质量、微博互动性、品牌因素和消费者的参与意愿在 0.01 水平上具有中度相关水平,同时也说明研究的测量题项收敛效果较好。
此外,自变量之间也有可能出现多元共线性现象,这会造成回归分析的参数值变异量不正常,为避免这种现象出现,还应该进行自变量之间的相关分析。因此,自变量相关矩阵中如果两个变量之间相关系数大于 0.75,说明两者之间存在共线性,二者不可以同时进入回归模型,应该选择一个相对重要的变量进入回归模型。【13】
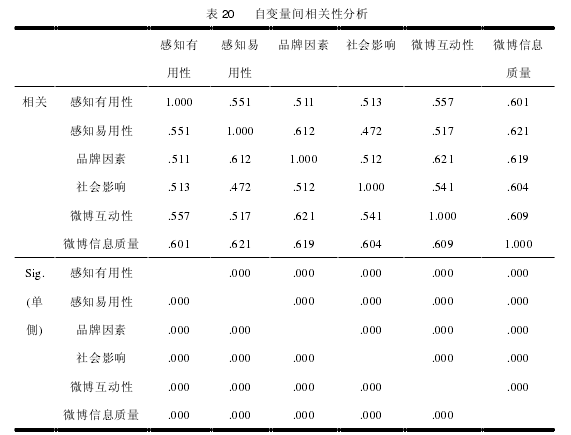
如表 20 所示, 感知有用性、感知易用性、社会影响、微博信息质量、微博互动性、品牌因素这 6 个自变量都是正相关关系(P<0.001),自变量之间相关系数没有大于 0.75,因此这六个自变量之间的共线性不明显,可以进行回归分析。
4.5 回归分析
回归分析是确定两种或两种以上变量间相互依赖的定量关系可以运用回归分析这一统计方法。上文的相关分析可以表明六个自变量因素和因变量之间存在关系的紧密程度,但是无法定量表明自变量和因变量之间的因果关系,因此采用多元回归分析。通过多元回归分析,可以筛查出对因变量最有预测力的自变量,并且定量算出自变量和因变量之间的关系。本文以参与服装设计师品牌微博营销意愿为因变量,感知有用性、感知易用性、社会影响、微博信息质量、微博互动性、品牌因素为自变量,通过逐步多元回归分析方法构建回归模型。【14】
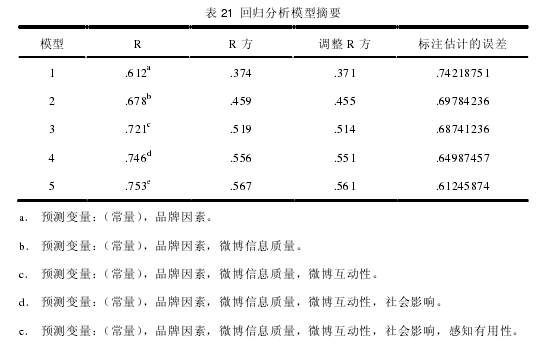
表 21 是感知有用性、感知易用性、社会影响、微博信息质量、微博互动性和品牌因素对服装设计师品牌微博营销参与意愿进行逐步回归分析,根据自变量对因变量预测能力的高低依次进入回归模型。模型 1 中,品牌因素这一自变量进入回归模型,品牌因素的解释量为 37.4%。模型 2 中,品牌因素和微博信息质量进入回归模型,两个因素的联合解释量为 45.9%,则微博信息质量的单独解释量是 8.5%。模型 3 中,品牌因素、微博信息质量、,微博互动性进入回归模型,三个因素的联合解释量为 51.9%,则微博互动性的单独解释量是 6.0%。模型 4 中,品牌因素、微博信息质量、微博互动性、社会影响进入回归模型,四个因素的联合解释量为 55.6%,则社会影响的单独解释量是 3.7%。模型 5 中,品牌因素、微博信息质量、微博互动性、社会影响、感知有用性进入回归模型,五个因素的联合解释量为 56.7%,则感知有用性的单独解释量是 1.1%。感知易用性没有进入回归模型,其他五个自变量对因变量预测能力的大小依据解释变异量由大到小为品牌因素、微博信息质量、微博互动性、社会影响和感知有用性。表 22 是 5 个回归模型及回归系数的显着性检验。回归系数在回归方程中表示自变量对因变量影响大小的参数。回归系数越大表明自变量对因变量影响越大,正回归系数表示因变量随自变量增大而增大,负回归系数标着因变量随自变量增大而减小。标准化回归系数消除了因变量和自变量所取单位的影响之后的回归系数。通过表 21,表 22,表 23 可知,本研究的五个自变量多元相关系数的平方和是 0.567,说明品牌因素、微博信息质量、微博互动性、社会影响和感知有用性共同解释服装设计师品牌微博营销参与意愿的 56.7%。这五个自变量对消费者服装设计师品牌微博营销参与意愿的预测能力由大到小分别是品牌因素、微博信息质量、微博互动性、社会影响和感知有用性,解释变异量分别是 37.4%、8.5%、6.0%、3.7%和 1.1%。感知易用性对消费者服装设计师品牌微博营销参与意愿的变异解释很小,没有进入回归模型。
本研究的标准化回归方程:服装设计师品牌微博营销参与意愿=0.211 ×品牌因素+0.204 ×微博信息质量 +0.201 ×微博互动性+0.187 ×社会影响+0.091×感知有用性
4.6 分析结果小结
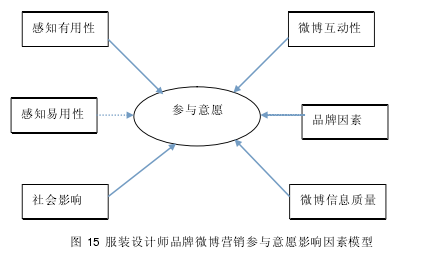
经过实证分析,影响服装设计师品牌微博营销参与意愿的因素,分别是品牌因素、微博信息质量、微博互动性、社会影响和感知有用性。感知易用性最终没有进入本文模型,这和初始研究假设不符。因此,如图 15 本文调整研究假设和模型,提出新的服装设计师品牌微博营销参与意愿影响因素模型。
4.6.1 研究假设检验
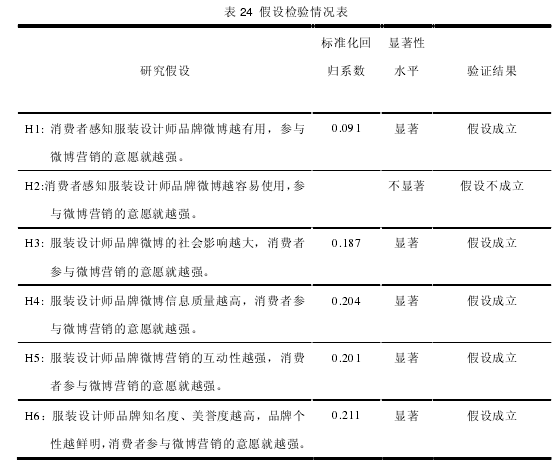
依据上文实证分析验证研究假设,表 24 是验证结果:【15】
4.6.2 研究模型修正
根据以上假设检验结果,修正模型如图 15。【16】