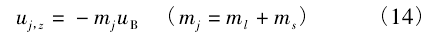3. 1 电子自旋
斯特恩 -盖拉赫实验对于解释反常塞曼效应并没有起到什么作用。当时物理先哲们对于反常塞曼效应提出的许多假设都显得徒劳。1925 年1 月,泡利提出不相容原理,这使得解答反常塞曼效应有了一丝希望(泡利和斯特恩两人关系密切,两人在理论与实验上相互促进[4])。这时,美国的物理学家克罗尼格(Rolph. L. Kronig)认为,“可以把电子的第四个自由度看成是电子具有固有的角动量,电子围绕自己的轴在做自转”[12]. 但泡利否定了他的想法,因为泡利认为第四个量子数应该用经典理论描述。克罗尼格很快就放弃了自己的想法[12]. 半年后,乌伦贝克和古德史密特受到泡利不相容原理的启发,提出电子具有自旋运动,并具有与电子自旋相联系的自旋磁矩,同年11 月,两人的论文因及时被他们的导师埃伦费斯特寄出而幸运的被发表在《自然科学》上[12].
根据空间量子化理论,磁矩与角动量的关系为:
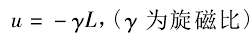
[1]. 轨道角动量磁矩的表达式为
它在 z轴方向上的分量只有两个值,
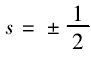
自旋对应着有自旋磁矩,类似轨道角动量磁矩导出自旋磁矩,即
ul为绕银原子运动的电子轨道角动量磁矩表达式,ul,z表示电子轨道磁矩在 z轴方向上的投影。 若不考虑自旋,银原子的角动量磁矩就等于绕银原子运动的电子的轨道角动量磁矩,即
1925 年,乌伦贝克和古德斯密特提出了电子自旋的假设,认为电子不仅有轨道角动量,还应该有自旋角动量,即
s 为自旋量子数,ms为自旋磁量子数,其在自旋的理论中只有
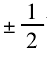
两个取值。由式(8)可知
则银原子的角动量磁矩为电子轨道角动量磁矩、电子自旋磁矩和原子核磁矩的矢量和,即
因为银原子的原子核轨道磁矩为电子自旋的千分之一,所以在式(13)中没有考虑银原子原子核的轨道磁矩。
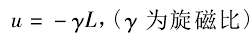 [1]. 轨道角动量磁矩的表达式为
[1]. 轨道角动量磁矩的表达式为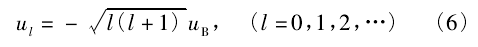
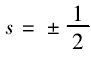 自旋对应着有自旋磁矩,类似轨道角动量磁矩导出自旋磁矩,即
自旋对应着有自旋磁矩,类似轨道角动量磁矩导出自旋磁矩,即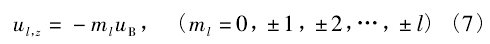

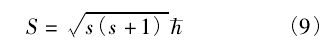
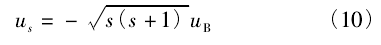
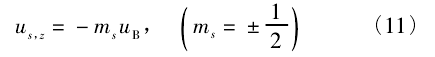
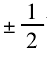 两个取值。由式(8)可知
两个取值。由式(8)可知