本文主要讨论了软物质体系的一些主要理论, 如弹性理论、相变理论、标度理论、自洽场理论、颗粒物质理论的发展历史和现状, 同时讨论了熵在软物质体系中的作用等。 大家在相关论文写作时,可以参考这篇题目为“软物质理论的研究现状与未来方向”的物理史论文。
原标题:软物质主要理论综述
本文主要讨论了软物质体系的一些主要理论, 如弹性理论、相变理论、标度理论、自洽场理论、颗粒物质理论的发展历史和现状, 同时讨论了熵在软物质体系中的作用等。 软物质体系中还有一些重要的动力学理论,如黏性问题、扩散问题、介面波的运动等问题均没有在本文中提及, 这些领域中也有一些软物质体系重要的理论研究工具和手法。
关键词: 软物质, 弹性理论, 标度理论, 自洽场理论。
1 引言
在经典体系中, 可以按照体系是否有演化的确定轨道分为确定体系与热力学体系, 确定体系从能量角度是朝相互作用总能最小的方向演化的。 热力学体系由于有环境涨落等的影响, 决定体系演化的不单是相互作用, 还有与体系自由度结构相对应的熵和所谓的环境温度, 这时体系的演化会沿着自由能也就是
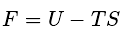
最低的方向演化。 一个体系是否是热力学体系, 取决于体系的相互作用总和(内能) 与熵的贡献TS的实力对比, 我们经常讨论的热力学体系发生在微观体系, 是因为室温对微观体系可以产生足够大的热力学涨落, 即, 使这个微观体系的熵不是很大, 也就是TS已经足够与相互作用内能大小相抗衡。
一个体系是热力学体系的先决条件, 就是熵对自由能的贡献不可忽视, 这就要求熵越大的体系越好, 多自由度的体系有相对较大的相空间维度和体积, 状态数比较大, 相应地就有较大的熵。 软物质的许多体系, 如聚合物、液晶等, 有一个特别相似的特性就是自由度比较大, 这时候体系的相空间积分就比较大, 对应的熵就比较大, 这使得即使在室温条件下, 体系的熵就可以起到重要甚至决定性的作用, 这时就有可能产生所谓的熵驱动现象。 软物质体系的易变形、易受外界刺激等特性其实都是熵驱动的某个侧面表现形式。
对软物质体系研究的发展过程中, 诞生了许多重要的理论方法, 最早的处理方式是平均场论。 在液晶理论的早期, Ginzburg-Landau 平均场论[1]在解释液晶的各种相变理论中起到了重要的作用。 然后是膜弹性理论, Helfrich 利用液晶弹性能的一种退化方式构筑了膜弹性[2], 这是膜理论最早的支撑点。 聚合物统计理论历来是软物质理论最重要的组成部分, 从最早的溶液中聚合物链的无规行走理论和分形, 到后来描述单链的“高斯链模型”, “半柔性蠕虫链模型”, 到受限体系的连续场方法处理--自洽场方法和密度泛函方法。 标度理论是软物质理论研究中的重要工具, 从聚合物链在自由空间的几何尺度, 到在受限空间的关联如聚合物刷、微管或通道中的聚合物链特性, 都离不开标度理论。 同时软物质体系经常带有电荷分布如何处理库仑相互作用就成为软物质理论计算的一个重要的技术手段。
2 软物质理论的背景与现状
2.1 液晶弹性理论
软物质体系液晶的分子场理论表述可以追溯到 Laudau 和 Lifshitz 1958 年提出 Gibbs 自由能的有序张量展开, 这种处理方法 1969 年由 de Gennes修 正 到 四 阶[3,4]. 在 1950 年 代 末 期, Maier 和Saupe[5-7]针对列型液晶提出了微观模型。 他们考虑了棒状非极性分子的范德瓦耳斯相互作用,并对其他分子的位置和空间取向进行平均, 得到了内部平均场。 Maier-Saupe 的平均场模型曾经遭到 Kaplan 和 Drauglis[8]的批评, 被认为是半唯象的平均场模型。 Chandrasekhar 和Madhusudana[9]通过进一步考虑了其他对称性的力, 推广了 Maier-Saupe 模型。
Onsager[10]通过引入一个与空间位置和取向都有关的势场, Onsager 理论的思想就是密度泛函理论的思想。 1973 年, Straley[11,12]对液晶的棒状统计理论模型进行了比较, 发现这些理论和 On-sager 对于较长的棒状分子组成的液晶是比较准确的, 能够与实验基本一致。
谈到液晶理论就不得不提曲弹性理论。 液晶 曲 弹 性 理 论 最 早 可 追 溯 到 Zocher[13]和 Os-een[14]1933 年的工作, 后来 Frank[15]于 1958 年进行了完善, 形成了后来广为人知的 Oseen-Frank 曲弹性能量表达式。 Oseen-Frank 的曲弹性理论是基于液晶中存在长程取向序的假设。 液晶与外场相互作用的研究, 导致了Fredericksz相变的发现[16], 也推进和加速了液晶作为显示工具的理论发展。
液晶理论避不开的一个话题是液晶缺陷的理论研究。 缺陷可以使自然形成的, 也可以是运用激光的方法人为产生[17-20]. Frank 借用了晶体中的概念来描述液晶中的线缺陷。 几种线缺陷都在20 世纪 60-70 年代有研究涉及[21-25]. 最近对缺陷的研究方法是用有效相互作用来代替缺陷周围的场。 也就是这些系统的弹性和统计力学可以用分立的拓扑 “电荷” 来表示[26]. 这里包含二维向列型液晶的点缺陷或三维向列型液晶的线缺陷以及三维体系中的点缺陷[27]. 对于双轴向列型液晶, 情况就要复杂得多[28-30], 由于分子对称性的降低, 导致了描述体系序参数的张量非零元素变少, 从而引起体系结构复杂度的增加。 传统的向列相就有可能分开为单轴向列相和双轴向列相, 其中单轴向列相位于各向同性相和双轴向列相之间, 但在特殊条件下会出现由双轴向列相向各各向同性相转变的朗道点或朗道线[28-31].
Helfrich 从液晶弹性理论出发, 提出了膜的自发曲率弹性模型, 在这个模型下, 膜弹性自由能可以表示为[32]
这里参数c0称为 Helfrich 自发曲率,kc称为膜的弯曲模量, 而
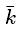
称为膜的高斯弯曲模量,H和K分别是膜的平均曲率和高斯曲率。 Helfrich 的自由能公式是一个泛函, Ouyang 和 Helfrich[33,34]通过变分,得到了决定膜形状的微分方程。
2.2 链弹性理论
高分子的统计物理起源于柔性模型, 它是把聚合物高分子当作一个没有任何弯曲刚度的柔性 “绳子”, 一个高分子的构型完全决定于单体之间的相互约束 (键能), 以及单体之间的几何约束, 它们之间贡献的相对大小决定了高分子链是高斯型构型或无规线团(random coil)。 当一个高分子的弯曲刚度足够大时, 被认为是半柔性的, 这时高分子链的构型变成尽可能让高分子链伸直的弯曲能和尽可能让高分子坍缩成无规线团构型熵以及单体之间的键能三者之间的竞争。 这种竞争导致了聚合物高分子链以及它们组成的聚集体的一些独特的性质[35,36]. 这种半柔性的特征也是决定高分子链如何缠绕形成交织网络 (cross-linked network) 以及这种网络的线性和非线性弹性和流动性的重要因素。 高分子的柔性有时也用相关长度来表示, 它是表征在布朗力作用下链表现出的能够 “伸直” 的长度。 如果把高分子链看成是可以弯曲的棒时, 相关长度描述的就是在棒低于这个长度时, 聚合物链相当于棒, 大于这个长度时, 相当于温度涨落起很大作用的柔性链。
生物高分子, 特别是由球粒型蛋白质组成的生物高分子, 通常比原子或分子尺度要大得多, 而且比一般人工合成的高分子要硬得多, 这种生物高分子是半柔性高分子模型的最好例子。 它们会显示出不同的弹性或黏弹性特征。
半柔性蠕虫链模型 (WLC)[37]是描述半柔性高分子链的最早模型之一, 早期的 WLC 仅仅局限于二维平面的变形, 后来慢慢地也把沿着链轴的扭转自由度考虑进来。 之后 WLC 模型又进一步被扩展到可伸长高分子半柔性WLC模型。
在很多生物高分子体系中, 单根的纤维可以缠绕(cross-linked)或者 “捆绑”(ligated) 在一起, 形成高分子捆, 如肌动蛋白。 这些捆状结构构成了真核生物细胞中的骨架。 传统的蠕虫链模型已经被证实不能简单地套用在这种体系中。 Heussinger 等[38]提出的蠕虫捆模型 (WLB) 可以较好地描述这种体系的离散构造特征和对应的内部变形模。 有一种观点认为, 用 WLB 模型可以比 WLC 模型更好地描述微管[39].

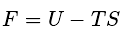 最低的方向演化。 一个体系是否是热力学体系, 取决于体系的相互作用总和(内能) 与熵的贡献TS的实力对比, 我们经常讨论的热力学体系发生在微观体系, 是因为室温对微观体系可以产生足够大的热力学涨落, 即, 使这个微观体系的熵不是很大, 也就是TS已经足够与相互作用内能大小相抗衡。
最低的方向演化。 一个体系是否是热力学体系, 取决于体系的相互作用总和(内能) 与熵的贡献TS的实力对比, 我们经常讨论的热力学体系发生在微观体系, 是因为室温对微观体系可以产生足够大的热力学涨落, 即, 使这个微观体系的熵不是很大, 也就是TS已经足够与相互作用内能大小相抗衡。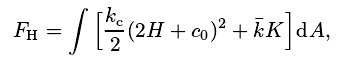
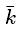 称为膜的高斯弯曲模量,H和K分别是膜的平均曲率和高斯曲率。 Helfrich 的自由能公式是一个泛函, Ouyang 和 Helfrich[33,34]通过变分,得到了决定膜形状的微分方程。
称为膜的高斯弯曲模量,H和K分别是膜的平均曲率和高斯曲率。 Helfrich 的自由能公式是一个泛函, Ouyang 和 Helfrich[33,34]通过变分,得到了决定膜形状的微分方程。




