对于八年级的学生而言,数学是一门十分重要的学科,八年级数学教学是初中的核心部分,也是承上启下的关键阶段。很多学生到了八年级会感觉到学习数学较为困难,对自身逻辑思维与问题分析能力有更多的要求。下面是搜索整理的八年级数学教学论文8篇,供大家借鉴参考。
八年级数学教学论文第一篇:八年级数学教材中概念严谨性缺失的案例分析
摘要:教材是教学的依据和蓝本,教材作为学科数学的重要载体,一个重要的目标就是要把数学知识的学术形态转化为教育形态。数学知识在学术形态和教育形态之间进行转换时,必须坚持严谨性和量力性相结合的原则。现行数学教材中少数概念界定,没有充分满足学生力所能及的量力性,严谨性存在缺失,制约了学生抽象素养的发展。数学教材中的概念界定及其遣词用句,应力求基于学生力所能及基础上的严谨,力求准确、简洁、避免歧义,力求体现数学概念的形成与发展;以助力师生的数学理解,助力提高教师概念教学设计的质效,助力学生数学抽象素养的发展。
关键词:抽象素养; 教材; 概念; 严谨性;
Textbook Case Study of Training Mathematical Abstraction Literacy:From the Perspective of Concept Definition
CHEN Jing'an YI Wenhui MENG Shengqi
Department of Mathematics,Guangdong University of Education The Institute of Teaching Research in Dongguan Dongguan No.1 Middle School
Abstract:Textbook is the basis and blueprint of teaching. As an important carrier of subject mathematics,textbook has an important goal to transform the academic form of mathematical knowledge into the educational form.When transforming the mathematical knowledge between academic form and educational form,we must adhere to the principle of combining rigorousness with strength. The definition of some concepts in current mathematics textbooks does not fully meet the students' capacity and the requirements of rigorousness,which hinder the development of students' abstract literacy. The definition of concepts and the use of words and sentences in mathematics textbooks should be based on the rigorousness within students' abilities,should be accurate,concise and unambiguous,and should also reflect the formation and development of mathematical concepts,so as to help teachers and students understand mathematics,improve the quality of teachers' conceptual teaching design and help students develop their mathematical abstraction literacy.
一、问题的提出
《高中数学课程标准(2017年版)》提出了六大核心素养,其中数学抽象是指通过对数量关系与空间形式的抽象,得到研究对象的素养(主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物背景中抽象出一般规律和结构,并用数学语言予以表征),并明确指出“数学抽象主要表现为:获得数学概念和规则,提出数学命题和模型,形成数学方法与思想,认识数学结构与体系。通过高中数学课程的学习,学生能在情景中抽象出数学概念、命题、方法和体系,积累从具体到抽象的活动经验……”[1]4-5。课标关于数学抽象素养的概念界定不仅清楚表明获得概念、提出命题、形成思想与方法、认识结构与体系等教学过程正是学生发展数学抽象素养的过程,而且其中提到三次关系、两次结构和体系,表明引领学生建立数学整体观对于发展学生数学抽象素养具有重要的意义。《义务教育数学课程标准(2011年版)》也强调:“教学方案是教师对教学过程的‘预设’,教学方案的形成依赖于教师对教材的理解、钻研和再创造。理解和钻研教材,应以本标准为依据,把握好教科书的编写意图和教学内容的教育价值”[2]50。因此,“教材作为教学的依据和蓝本,尤其是教材中数学概念的界定、遣词用句和内容编排及其反映的严谨性对于教师的教材分析、教学设计和教学组织有没有影响?具有怎样的影响?”直接决定了数学概念教学中数学抽象素养目标的落实与达成。为此研究者应用文献研究法、课堂观察法和案例分析法,基于数学教学和数学教材编写“严谨性和量力性相结合”原则的视角,对人教版数学教材中的几个概念课题,进行培养数学抽象素养的教材案例分析,旨在抛砖引玉、引发教材编写者和教学同行们的思考,使教材的编写与研究更好地引领教师培养数学抽象素养的教学实践。
二、关于严谨与量力相结合的教学原则
正如《高中数学课程标准(2017年版)》指出的:“数学是研究数量关系与空间形式的一门科学。数学源于对现实世界的抽象,基于抽象结构,通过符号运算、形式推理、模型构建等,理解和表达现实世界中事物的本质、关系和规律”[1]1。其中,科学指分科的系统知识;抽象则是确定和抽取事物的本质属性而舍弃其非本质属性的思维方法,简而言之就是透过现象看本质。特别地,数学抽象是舍弃事物即思维对象的其他非数学本质特性,抽取其数量关系或空间形式的本质特征,并加以概括,最终形成数学概念与结论的过程。概括是把从若干个别事物抽象出共同属性,推广到同类事物中去的思维过程。抽象和概括是互相联系、不可分离的,数学的抽象程度越高,概括性就越强,应用范围也越广。随着数学的发展,数学的抽象呈现为逐级抽象、多次抽象。因此数学具有高度的抽象性、逻辑的严谨性、应用的广泛性等特点。抽象性和严谨性特点在数学科学的知识体系中具体表现为严密的公理化系统,即从尽可能少的未经定义的原始概念和一组不证自明的原始命题出发,运用纯逻辑演绎方法———具体而言就是概念必须定义、命题必须证明建立起来的演绎系统。因此,数学教材编排与教学设计组织中是否注重和落实这个严谨性、系统性特点,对于培养和发展学生的数学抽象素养具有直接的影响。
但是,由于中小学数学教学的对象大多是青少年,而青少年的认知结构、思维水平等存在发展的阶段性特点,使得作为连接数学与中小学学生的数学教材中的数学概念和命题体系难于或不能完全按数学科学的严谨性来呈现。这清楚地表明,中小学数学教材与生俱来的数学与教育双重属性的特点,决定了中小学数学教材的编写和数学课堂教学的设计与组织势在必然地产生数学的严谨性与学生的量力性匹配的问题。因此,作为连接数学科学和中小学学生的桥梁,严谨和量力相结合的原则———即在学生力所能及的基础上尽可能的严谨,不仅是数学课堂教学的基本原则,也是数学教材的编写原则,是数学教材的编写和数学课堂教学设计与组织的应然要求和必然结果。换言之,在数学教材的编写、数学教学活动的设计与组织中,都要依据严谨性和量力性相结合的原则,在学生力所能及之处保证数学的严谨性,在学生力所不及之处适度淡化严谨性[3]。然而,课堂观察及教材分析中发现,中学数学教材中某些数学概念界定的严谨性则是在学生的力所能及范围内而有所缺失、亟待加强的。
三、中学数学教材中概念严谨性缺失的案例分析
众所周知,数学逻辑严谨性的要求,概念必须定义,命题必须证明。概念是反映事物本质属性的思维形式。数学概念则是反映空间形式与数量关系本质属性的思维形式。一个概念所反映对象的本质属性叫做这个概念的内涵;内涵是对概念质的规定。而概念所反映对象的全体组成的集合叫做概念的外延。换言之,概念由内涵与外延构成,内涵不同则概念相异。例:两组对边分别平行的四边形叫做平行四边形;仅有一组对边平行的四边形叫做梯形。中小学数学教材由于受学生思维水平的限制,有的数学概念会采用不严格的描述性代替。因此,中小学数学概念严谨性的标准是概念的界定与表述应在学生力所能及即量力性的基础上达到最大化的严谨。倘若某个数学概念的表述,没有充分满足学生的量力性(教材中对这个数学概念呈现的严谨性再高一些,学生是能接受的),则认为这个数学概念的严谨性是有缺失的。
(一)九年级教材中圆周角概念的严谨性分析与再建构
基于这个标准,首先对课标人教版九年级上册教材中圆周角概念的严谨性进行分析,其次尝试对圆周角概念进行再建构。
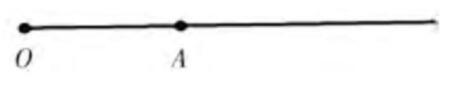
人教版九年级上册将圆周角概念界定为:“顶点在圆上,并且两边都与圆相交的角叫做圆周角”[4]。这个概念是否严谨呢?这首先需要弄清楚角和边的概念。依据七年级教材“有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两边”[5]132。而七年级教材在四年级教材“把线段向一端无限延伸就得到一条射线。射线只有一个端点”[6]的叙述基础上,对射线的界定是:“用图1的方式来表示射线OA,其中点O是射线的端点”[5]126。由此概念界定可知,射线是包含端点的,而角是由射线组成的,所以角这个图形是包含端点的。
图1 射线OA
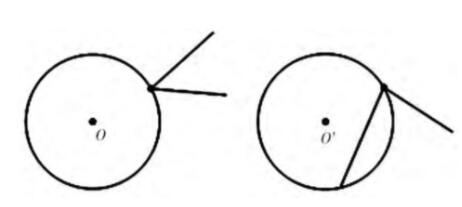
那么,图2所示的两个角是圆周角吗?
教材判定图2所示的两个角都不是圆周角。但是,爱钻研的学生依据概念会发现自己的判断与教材中给出的答案是相悖、矛盾的。首先,图2所示这两个角的顶点都在圆上;其次角的两边是射线,而射线是包含端点的,所以这两个角的两边分别和圆都是相交的(与圆相交于两条射线公共的端点)。因此,这两个角都满足圆周角的概念,所以它们都是圆周角。
上述悖论说明,教材中圆周角概念的严谨性有明显的缺失。不仅如此,这个概念还制约着后续圆周角的定量研究。即图2这样的所谓圆周角的大小不满足圆周角定理的条件与结论:圆周角等于同弧所对应的圆心角的一半。
进一步地,由概念内涵与外延的反变关系并结合以上分析不难发现,悖论来自圆周角概念界定的严谨性缺失,导致其外延包含了图2这类本质属性有所缺失的角。要消除悖论,必须增加本质属性、进行圆周角概念的重构,以剔除图2这类特殊的角———即两边和圆相交于射线的公共端点的角。为此,对圆周角的概念进行以下再建构就势在必然:顶点在圆上,且两边与圆相交于顶点之外的两个点所构成的角叫做圆周角。
实践证明,九年级的学生,其思维能力、认知水平都有了长足的发展,对圆周角概念进行科学、严谨的界定,既切实必要而又充分可行。
图2 圆周角的判断
(二)八年级教材中分式概念的严谨性分析与再建构
大纲人教版八年级上册对分式的概念界定是:“一般地,整式A除以整式B,可以表示成
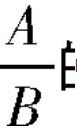
的形式。如果除式B中含有字母,那么称
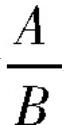
为分式(fraction),其中A称为分式的分子,B称为分式的分母”[7]。在《现代汉语词典》中“可以”一词的解释是:许可。细细体会,它有“这样也行,不这样也行”、即数理逻辑中“或命题”的选择含义。回到分式概念中的“可以”一词,其意义是:整式A除以整式B,可以选择性地表示成
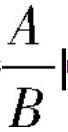
的形式,也可以不表示成
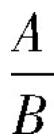
的形式。但事实上,不表示成
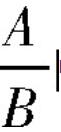
的形式,而是表示成A÷B的形式,例如x÷y就不是分式了。因此,该概念的严谨性是有所缺失的。缺失的主要原因是:概念叙述中,用词的歧义造成了不严谨。本质上混淆了概念界定中本质属性“合取”与“析取”的逻辑认知与文字语言表达,其结果不仅违反了抽象逻辑思维必须遵循的同一律:A是A,同时也违反了矛盾律(A不是非A)和排中律(A与非A不能同真)等逻辑规律。
针对以上分式概念中差之毫厘谬以千里的问题,课标2013年6月第一版人教版教材或许发现了这个问题,它将分式概念中发生歧义引起严谨性缺失的地方重新进行了如下编排:“如果A、B表示两个整式,并且B中含有字母,那么式子
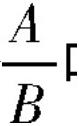
叫做分式(fraction)。分式
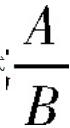
中,A叫做分子,B叫做分母”[8]。这就避免了歧义,为分式概念严谨性教学设计提供了便利条件。但遗憾的是,同时又舍弃和缺失了分式来源于整式相除、并且类比分数相除的表达的概念形成和发展过程。
事实上,由于大纲人教版教材中分式概念界定使用了有歧义的“可以”一词导致其严谨性缺失,因此概念再建构时,只须用意义明确的“并且”去替换“可以”一词即可:“整式A除以整式B,并且表示成
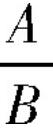
的形式。如果除式B中含有字母,那么称
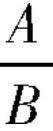
叫做分式(fraction),其中A称为分式的分子,B称为分式的分母”。如此定义分式,既避免了歧义,又保留了分式来源于整式相除并且类比分数表达的概念形成与发展过程。
(三)高中教材中任意角概念界定的缺失及其对教师概念理解与教学组织的影响
1.人教版高中数学必修4第一章第一节“任意角”的教材分析
数学的严谨性主要表现为概念必须定义、命题必须证明。但遗憾的是,课标人教版高中数学必修4教材第一章“任意角的三角函数”中却没有给出任意角的概念。而任意角是后面弧度概念和“任意角的三角函数”的铺垫性基础知识。因此,教学中,具有教材分析能力和数学抽象素养的教师会对任意角的概念进行再创造。
事实上,深入分析高中必修4第一章第一节“任意角”课题,不难发现其中不仅包括按照射线的旋转方向划分而产生的正角、负角、零角及任意角,还包括按照终边所在位置划分而产生的象限角、轴线角、终边相同的角,以及角的始边、角的终边共9个相关概念(7个角概念和2个边概念),因此这是一节典型的概念教学课。只有掌握这些概念,学生才能提高计算与判断终边相同的角的技能。
这些新知识的生长点也就是学生已有认知结构,不仅与小学和初中的角概念、角的大小比较和角的范围有关,也与坐标系、象限、轴线有关。这些生长点的内容非常丰富,关系交错复杂。其教学设计考验着教师对9个概念形成的因果先后等内在逻辑关系的认知与揭示,以及对于几何教学必然蕴含的数形结合、观察、比较的思想方法的认知与揭示,以及类比数系从自然数扩充到正数、负数的建构,产生正角、负角、零角,以及类比七年级整数和分数统称为有理数的外延式定义去再创造与建构任意角的概念,进而应用数形结合、抽象概括等思想方法获得象限角、轴线角、终边相同的角等创造活动[9]。
2.“任意角”教材对于教师理解任意角概念及其教学设计与教学组织的影响
《普通高中数学课程标准(2017年版)》在教材编写建议中强调“教材的编写既要充分反映数学的本质,体现数学的逻辑性与严谨性,也要符合高中生的认知规律。教材不能只是数学结论的简单表述,应该体现结论产生的背景和形成发展过程,引导学生在背景和过程中主动探究、认识建构、理解结论”[1]94。对于任意角课题能否从课题包含的9个概念、概念之间的内在逻辑先后关系、概念形成发展过程中蕴含的思想方法这3个方面清晰剖析与理解,不仅反映了教师对数学概念的形成发展过程以及其中蕴含的思想方法的认知、理解与掌握,而且反映了教师对数学知识整体和本质的理解,以及教师对概念界定的内涵式定义与外延式定义等逻辑知识的应用及其蕴含的抽象素养。
为此,研究者设计了以下问题串,并以某省普通高中数学教师职务网络培训专题研讨的形式进行了问卷调查:“针对高中数学必修4的1.1.1任意角第一课时,请您分析解答以下问题:(1)该课题教学是不是概念教学课?(2)教科书中并没有定义任意角,请问什么是任意角?(3)该课题包含哪些概念与哪些角?(4)请按照教科书中这些概念发生发展的过程,梳理出这些概念之间的逻辑顺序或概念网络图,并分析其中蕴涵的数学思想与方法。(5)请界定这个课题具体的三维教学目标”。研究者考虑到网络培训的需要,在该专题研讨网络发布2周后,以答疑辑要的形式提供了上述问题的参考解答。
为了进一步调研任意角课题的教学现状,运用课堂观察法,研究者还对沿海地区与民族贫困地区重点高中6节任意角课题的课堂教学进行了观摩实录;运用访谈法,对任教的4位教师(包括一位资深特级教师)进行访谈。在分析教材的基础上,研究者对教师的教案以及课堂教学的观察和问卷调查进行分析和研究。
问卷调查结果显示,有近30%的教师不能确定这是一节概念教学课;超过50%的教师既不能解答任意角的概念,也不能明确指出7个角概念及这些概念发生发展的内在逻辑先后顺序及其蕴含的思想方法。虽然调查问卷中明确了任意角指的是高中数学必修4中第一章第一节第一课时的内容,问题聚焦、要求清晰、表述准确,但是调查问卷结果显示,在问卷解答的教学目标界定中,近40%的教师不明题意、似是而非,甚至将任意角与第一章第一节第二课时的弧度、整个第一章任意角的三角函数混在一起讨论、回答问题,由此可见这部分教师对于概念及其蕴含的数学思想方法的理解存在困难、教师专业发展的意识亟待加强。
课堂观察发现,教师教学中大都重视正角、负角和零角的概念认知与建构,不重视象限角、非象限角(也称轴线角)、终边相同的角的概念认知与建构。观察的6节课既没有教师解释何为任意角,也没有教师解释为什么要把角放在坐标系里研究。教学与例习题的重点是判断象限角和终边相同的角、终边相同的角的计算及集合表示等技能掌握上。特别地,访谈授课教师“什么是任意角”,没有教师能够准确回答,有的教师竟然回答“随便一个角就叫任意角”“我认为不是每一个概念都需要定义的,所以任意角不一定要定义”。另外,针对答疑辑要教学目标中的化归思想方法,提问:任意角教学中化归思想体现在哪里?值得一提的是,问卷调查的统计显示,有个别教师能够正确阐述本课题包括7个角概念以及7个角概念形成的先后顺序:正角、负角、零角、任意角、象限角与轴线角、终边相同的角,以及7个角概念建构中蕴涵的数形结合、分类讨论和类比、化归等思想方法[10]。
四、研究结论与思考
(一)概念严谨性缺失对于教师课前教材分析与教学设计的影响
现行数学教材编写中既存在部分概念界定及其遣词用句严谨性缺失和不够准确、简洁的情形,也存在部分概念编排不符合数学知识发展和学生的认知规律。例如课标人教版教材高中数学必修一第二章,对于五类基本初等函数中前三类的编排顺序是指数函数、对数函数、幂函数,这与数学认知规律由易到难、由具体到抽象,即学生先学习相对低级和具体的乘方、开方运算,进而到相对抽象复杂的指数对数运算的逻辑顺序相背离。研究者在教师培训中也发现,这样编排造成一线数学教师对于这三类函数概念教材的理解和教学设计产生困惑与混乱[11]。又如课标人教版七年级教材关于数轴的定义从过去言简意赅的“规定了原点、方向和单位长度的直线叫做数轴”,改成冗长累赘的四段文字表述,对于七年级学生而言既无此啰嗦赘述的必要,更无助于培养学生数学抽象素养。教材编写中概念呈现排版逻辑上的无序与概念界定及其遣词用句严谨性的缺失,一方面,不仅增大了教师备课的时间成本、考验着教师对数学对象的本质理解和数学再创造能力,另一方面又直接制约了教师的教材分析、教学设计的质效,进而影响了学生在概念学习中数学抽象素养的发展。事实上,《普通高中数学课程标准(2017年版)》在教材编写建议中明确提出“编写者要认真研究如何在数学内容的表述中体现数学学科核心素养,编写出数学内容与数学学科核心素养融为一体的教材”[1]92。因此,如何在教材编写中适切地解决这些问题,尤其在新版课程标准教材的概念内容修订中落实数学抽象素养的发展无疑是亟待研究的问题。
(二)教材中概念界定严谨性缺失对于教师课中教学组织与实施的影响
《义务教育数学课程标准(2011年版)》提出“教师应揭示知识的数学实质及其体现的数学思想,帮助学生厘清相关知识之间的区别和联系等。数学知识的教学,要注重知识的‘生长点’与‘延伸点’,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性”[2]45。课堂观察及其观评课研讨活动分析显示,教材中概念界定严谨性的缺失对于教师的课堂教学组织与实施带来以下5个方面直接或间接的影响与困难:制约着教师对概念本质属性的认知、理解及其教学组织;制约着教师引领学生对新旧概念本质属性的联系与区别的认知和探究;制约着教师对于概念形成发展过程中蕴含的数学思想方法的认知与揭示;助推了传统重知识、轻方法,重结果、轻过程,概念教学蜻蜓点水、不痛不痒,沉溺于题海战术的观念与传统做法,导致概念建构半生不熟、本质属性认知零碎,学生思维负担减负困难;制约教师对概念教学目标的精准界定和数学整体观的建立,制约着教师运用数学课程标准的理念、目标、要求指导自己的教材分析和教学设计、组织、反思评价,以致增加了概念教学中数学核心素养及其所反映的三维目标界定与达成的难度。
五、教材编写建议与启示
(一)中小学数学教材编写应遵循学生的认知发展规律和严谨与量力相结合的原则,并力求体现数学概念的形成与发展过程
教材是教学的依据和蓝本。中小学数学教材作为学科数学的主要载体,一个重要的目标就是要把数学知识的学术形态转化为教育形态。数学知识在学术形态和教育形态之间进行转换时,既要遵循由易到难、由具体到抽象、由低级到高级等学生认知规律,还要坚持严谨性和量力性相结合的原则,力求体现数学概念的形成与发展过程,将课程标准提出的课程目标和发展学生数学核心素养的目标转化为实际的教学要求,“编写出数学内容与数学学科核心素养融为一体的教材”,以助力师生在背景和过程中主动探究概念所指对象的本质属性、能动建构概念、进而理解和掌握概念,发展抽象素养。否则,不仅增大了教师备课的时间成本、考验着教师对于数学对象的本质理解和数学再创造能力,又直接或间接地制约了教师的教材分析、教学设计的质效,进而影响着学生数学学科核心素养的发展。
(二)教材编写中要重视和加强概念界定及遣词用句的严谨性表达,助力学生抽象素养的发展
数学概念是反映空间形式和数量关系本质属性的思维形式。一个数学概念的内涵和外延分别从质和量两个方面刻画和规定了这个概念,每个概念都是其内涵与外延的统一体。概念的内涵严格确定了概念的外延,反之,概念的外延也完全确定了概念的内涵[12]。因此,概念之间是彼此互相区别、界限分明的,不容混淆,更不容互换。这就在客观上明确要求数学概念的教材编写应重视和加强对概念界定严谨性的研究与分析,并且在数学教材的概念界定及其遣词用句中,应力求基于学生力所能及基础上的严谨,力求准确、简洁、避免歧义。这不仅是助力师生对概念和数学本质的理解,助力教师提高概念教学设计和教学组织的质效,而且也是助力学生数学抽象素养发展不可或缺的重要保障。
参考文献
[1]教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
[2] 教育部.义务教育数学课程标准(2011年版)[M].北京:人民教育出版社,2012.
[3]王建磐.历史视角下的数学素养:讲好我们的故事[J].数学教育学报,2019(3):1.
[4] 课程教材研究所,中学数学课程教材研究开发中心.义务教育课程标准实验教科书数学九年级上册[M].北京:人民教育出版社,2014:85
[5] 课程教材研究所,中学数学课程教材研究开发中心.义务教育课程标准实验教科书数学七年级上册[M].北京:人民教育出版社,2012.
[6] 课程教材研究所,小学数学课程教材研究开发中心.义务教育教科书数学四年级上册[M].北京:人民教育出版社,2014:38.
[7] 人民教育出版社数学编辑室.九年义务教育三年制初级中学代数第二册[M].北京:人民教育出版社,1994:40.
[8] 课程教材研究所,中学数学课程教材研究开发中心.义务教育课程标准实验教科书数学八年级上册[M].北京:人民教育出版社,2013:127.
[9] 课程教科书研究所,中学数学课程教材开发中心.普通高中数学标准实验教科书:数学4(必修)[M].北京:人民教育出版社,2007:1-5.
[10] 陈静安.基于数学素养的教师教材分析策略研究[J].中国人大报刊复印资料《高中数学教与学》,2017(6):47-51.
[11]陈静安,方丽.高中数学必修1难点概念启发式教学策略[J].教学与管理,2014(11):53-54.
[12]陈静安,曾志红,刘云,等.课堂教学中的数学活动经验研究:问题与对策[J].广东第二师范学院学报,2017,37(3):107-112.
八年级数学教学论文第二篇:八年级数学课堂中以惑为诱教学法的运用探析
摘要:随着社会教育事业的迅速发展,初中数学教学发生了巨大的变革,特别是课堂教学方式的改革。本文主要探究了以“惑”为诱的教学模式,教师通过充分地利用“惑”来进行教学设计,逐步引导学生自主地探究学习。文章主要以八年级的数学教学为例,对以“惑”为诱的教学模式进行详细的阐述。
关键词:八年级数学; 以惑为诱; 教学模式;
引 言
随着课程改革的不断深入,课堂教学的理念也发生了翻天覆地的改变,新课程改革倡导的是以学生为主体的教学,推翻了以往的以教师为主体的教学。新课程注重的是激发学生的学习兴趣、热情及创造力等,要以学生为主体作为前提条件,在此条件下产生了以“惑”为诱的教学模式,进而提高了八年级的数学课堂教学效率。
一、以“惑”为诱在八年级数学教学应用中的具体要求
(一)创建有效的主题情境——以“惑”为主
激发学生感情体验的基础就是情境,让学生产生良好的感情体验,引发学生的兴趣,这就是创建情境的目的,它可以使学生了解人物、事实、自然、事件、社会等,可以使学生与所处的现实世界进行更好的交流,从而增强学生的求知欲望[1]。
在数学教学当中,数学情境是指从学生的生活习惯和现有的生活社会背景出发,从学生在平时所经历、了解的一些事件出发,如社会问题、生活事件、人物故事及一些关于数学的典故,设置一些数学问题以及概念等。简单来说,就是学生进入接触数学活动的环境,产生学习数学的行为条件。
在课堂的实际教学当中,教师所提出的问题,是联系教师、学生和教材的纽带。这种方式也是一种重要的教学手段,可以说是一种较为完善的教学手段。我们创建“惑”的情境就是为了激发学生的学习兴趣,在我国素质教育改革与基础教育课程改革的过程当中,课堂教学中的提问变得越来越重要。而提问是学生对知识的好奇和怀疑的开始,是从原有的固定教学模式向着“以学生为中心”转变的开始。课堂提问对学生启发思维、开发潜能、巩固知识及培养综合素质等有着重要的作用,因此课堂提问在现阶段的教学当中也受到了越来越多的重视。
在创设的“惑”的情境中,教师对学生提出的问题一定要有一定的坡度,并且符合学生的知识水平,从而给学生造成一定的认知冲突,促使学生保持积极的思考状态。提问的难度较大时,教师需要逐步来引导学生,使学生对数学知识产生困惑,也让学生在面对“惑”时有自信能够解决,进而对数学知识理解得更加透彻;另外,教师在创设以“惑”为主的教学情境时,需要根据学生的实际情况,设立难度适中的疑惑,既要能激发学生对知识的求知欲望,又不能让学生因为太难而失去信心。
(二)注重在“惑”的教学中体现学生的个体性,提高其参与度
数学的方法、思想及知识,必然是通过学生在数学实践活动当中掌握和理解的,并不是单纯地依赖教师的讲解获得的。教师需要在教学实践当中灵活地运用“数学情境”,即引导学生亲身投入到“数学情境”的活动当中,使学生在手做、耳听、眼观、口说、脑想的过程当中,增长智慧、积累知识、培养能力。这不仅可以使学生从动作过渡到思维,还可以保证学生在教学过程中的主体地位。例如,在“有理数的减法”教学中,教师可引导学生观察篮球比赛的实例,组织学生以小组为单位讨论净胜球的可能情况,并把其所观察的结果用数学式子表达出来,最后利用数学式子归纳、总结。
学生的数学学习能力是参差不齐的,在统一的以“惑”为诱的情境教学中,有的学生觉得太过容易,而有的学生则感觉太难,这对学生的学习都是不利的。因此,教师在应用“惑”的教学模式时,需要对不同水平的学生,设定不同的“知识疑惑”,以便更加充分地照顾到每一位学生。这就要求教师要充分了解每一位学生的困惑在哪里,然后逐步地引导学生,为学生解惑,提高学生的数学学习效率。
(三)提倡学生自主探究
学生在以“惑”为诱的教学过程中起着重要的作用,在自主学习的过程中学生要学会自我解惑。“惑”的创建,是要让学生亲身去了解知识、发现问题,产生探索知识的欲望,只有这样,学生才能对所学的知识有更加深入的理解与掌握。教师设置“惑”是为了让学生在学习的过程中学会质疑,然后自主地去探究真理,这可以更好地激发学生的求知欲望,从而进一步提高学生的学习效率及学习的兴趣。在教学过程当中,教师要引导学生将抽象的知识与生活中一些形象生动的事件整合起来,从中启发学生的思维模式并且学习规律性的知识。
(四)教师要重视自身的引导作用和处理技巧
学生在实际的生活当中,遇到的情景是比较复杂的,如果按照原有的模式呈现给学生,那么,学生很可能会受到一些不好的影响,会很大程度地限制时间、空间、知识、能力。在解惑教学的过程中,教师允许学生出现失误,但是,若是学生反复出现失误,则需要引起教师的重视,并及时进行引导。在引导的过程中,教师需要站在学生的角度考虑问题,尊重学生,和学生一起进行探究。
二、以“惑”为诱在八年级数学教学应用中的具体案例
以多边形的内角和的计算为例,应用以“惑”为诱的教学模式进行授课。
首先,提出问题。在以往学习的课程中知道正方形及长方形的内角和是360°,而三角形的内角和是180°,在这里,教师可以向学生提问:不规则的四边形的内角和是多少?可以用已学的知识进行论证吗?教师给出问题,学生会有些困惑,会猜想答案,学生产生疑惑的过程,就是以“惑”为诱的教学模式的第一步。
其次,教师与学生一起思考该疑惑。教师需要引导学生,给学生提出问题:求不规则四边形的关键在哪里?难点在哪里?教师引导学生将未知的问题想办法转化为学过的、已知的知识。学生在此过程中,会有自己的答案,教师可以让学生进行分组讨论,然后总结学生给出的答案,并从不同的角度去分析,然后总结出最终的解决方案。
再次,教师在此问题上进行延伸。学生已经探究出了不规则四边形的内角和的解决方法,教师提出问题,超过四边的多边形的内角和如何求解?除了将多边形分解成多个三角形求其内角和之外,还有别的解决方案吗?然后,教师给学生一定的时间,让学生自己去探究,在探究完成之后,让学生自主地总结出多边形内角和的规律,及n边形的内角和为(n-2)×180°,同时,学生在以后的学习过程中即使忘记了这个内角和的求解公式,也可以自己去推理。同时,学生既解决了疑惑,还牢牢地记住了推理过程,对该知识的理解与记忆达到了新的高度。
最后,学生进行总结与反思。学习知识的过程中,学生要学会不断地反思。在反思的过程中,学生可以总结自己在学习的过程中所犯的错误,以及在思考的过程中欠缺的地方。通过反思,学生以后在遇到类似的问题时,就能够从容地面对,并且从多角度出发进行思考。
结 语
综上所述,在八年级数学教学的过程中,教师在应用以“惑”为诱的教学模式时,要尽量避免该种教学模式的弊端,要时时刻刻关注学生在整个过程中的表现,要照顾到班级里的每一位学生。在学生遇到难度较高、难以解决的困惑时,教师要进行引导,从学生的角度思考问题,进而提高八年级数学的教学效果。
参考文献
[1]张建飞.以“惑”为诱教学方法在八年级数学教学中的应用研究[J].教育观察(下半月),2014(13):53-55.
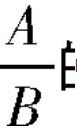 的形式。如果除式B中含有字母,那么称
的形式。如果除式B中含有字母,那么称 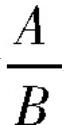 为分式(fraction),其中A称为分式的分子,B称为分式的分母”[7]。在《现代汉语词典》中“可以”一词的解释是:许可。细细体会,它有“这样也行,不这样也行”、即数理逻辑中“或命题”的选择含义。回到分式概念中的“可以”一词,其意义是:整式A除以整式B,可以选择性地表示成
为分式(fraction),其中A称为分式的分子,B称为分式的分母”[7]。在《现代汉语词典》中“可以”一词的解释是:许可。细细体会,它有“这样也行,不这样也行”、即数理逻辑中“或命题”的选择含义。回到分式概念中的“可以”一词,其意义是:整式A除以整式B,可以选择性地表示成 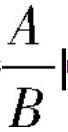 的形式,也可以不表示成
的形式,也可以不表示成 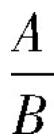 的形式。但事实上,不表示成
的形式。但事实上,不表示成 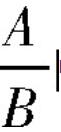 的形式,而是表示成A÷B的形式,例如x÷y就不是分式了。因此,该概念的严谨性是有所缺失的。缺失的主要原因是:概念叙述中,用词的歧义造成了不严谨。本质上混淆了概念界定中本质属性“合取”与“析取”的逻辑认知与文字语言表达,其结果不仅违反了抽象逻辑思维必须遵循的同一律:A是A,同时也违反了矛盾律(A不是非A)和排中律(A与非A不能同真)等逻辑规律。
的形式,而是表示成A÷B的形式,例如x÷y就不是分式了。因此,该概念的严谨性是有所缺失的。缺失的主要原因是:概念叙述中,用词的歧义造成了不严谨。本质上混淆了概念界定中本质属性“合取”与“析取”的逻辑认知与文字语言表达,其结果不仅违反了抽象逻辑思维必须遵循的同一律:A是A,同时也违反了矛盾律(A不是非A)和排中律(A与非A不能同真)等逻辑规律。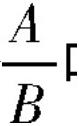 叫做分式(fraction)。分式
叫做分式(fraction)。分式 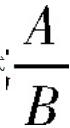 中,A叫做分子,B叫做分母”[8]。这就避免了歧义,为分式概念严谨性教学设计提供了便利条件。但遗憾的是,同时又舍弃和缺失了分式来源于整式相除、并且类比分数相除的表达的概念形成和发展过程。
中,A叫做分子,B叫做分母”[8]。这就避免了歧义,为分式概念严谨性教学设计提供了便利条件。但遗憾的是,同时又舍弃和缺失了分式来源于整式相除、并且类比分数相除的表达的概念形成和发展过程。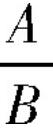 的形式。如果除式B中含有字母,那么称
的形式。如果除式B中含有字母,那么称 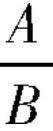 叫做分式(fraction),其中A称为分式的分子,B称为分式的分母”。如此定义分式,既避免了歧义,又保留了分式来源于整式相除并且类比分数表达的概念形成与发展过程。
叫做分式(fraction),其中A称为分式的分子,B称为分式的分母”。如此定义分式,既避免了歧义,又保留了分式来源于整式相除并且类比分数表达的概念形成与发展过程。





