5-8年级学生数学问题解决能力的不足及建议

八年级数学教学论文第三篇：5-8年级学生数学问题解决能力的不足及建议

 

　　摘要：通过构造学生数学问题解决能力的测评框架，对某地区五至八年级的1734名学生进行分层抽样测试。结果显示，学生数学问题解决能力存在“两极分化”现象；策略使用的倾向性和合理性水平存在差异；数学表达的表征形式和清晰程度存在差异。由此提出建议：重视“两极分化”现象；强调高层次数学思维融入；鼓励数学表达；依托数学核心素养进行教学转型。

 

　　关键词：数学问题; 解决能力; 策略使用; 数学表达; 核心素养;

 

　　An Empirical Study on the Mathematical Problem Solving Competency of Students at Grade 5 to Grade 8——In the Case of “Law-exploring Questions”

 

　　Gao Xiang Xu Binyan

 

　　一、为何再度聚焦数学问题解决能力？

 

　　2016年9月，中国学生发展核心素养研究成果发布，提出了3大方面、6大素养、18个基本要点，其中明确提出“问题解决”为基本要点之一[1]。具体到数学学科，我国《义务教育数学课程标准（2011年版）》将“问题解决”作为数学课程目标的总目标之一[2]。2017年，我国教育部颁发《普通高中数学课程标准》，明确将数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析素养培养的最终目的指向了学生数学问题解决能力的提升，将学生的数学问题解决能力推向了一个新的高度。

 

　　我国对于学生数学问题解决能力的培养也有着悠久的历史和丰富的经验，但学生数学问题解决能力的现状仍不容乐观。顾泠沅于1990年和2007年两次对初中二年级学生进行数学教学目标的分水平测试，发现学生在体现分析问题和解决问题能力的“分析——探究性理解”水平尚无明显提高，甚至出现了一定的下降[3]。放眼国际评测项目PISA，我国学生能达到体现数学问题解决能力最高水平的“数学精熟度”6级的人数比例从2012年的30.8%直线下滑至2015年的9.0%（数据来源：OECD,PISA2012,2015 Database），再度聚焦学生数学问题解决能力刻不容缓。

 

　　本文拟通过测评五至八年级学生数学问题解决能力现状，揭示学生数学问题解决能力的发展特点，探索提升学生数学问题解决能力的教学建议。

 

　　二、数学问题解决能力的相关研究

 

　　（一）数学问题解决能力内涵的研究

 

　　美国数学教师理事会（NCTM)2000年发布的《学校数学教育的原则和标准》中给出了十条有关数学理解和能力的标准，其中“数学问题解决能力”要求K-12年级的学生能“通过解决问题掌握新的数学知识”、“解决在数学及其他情境中出现的问题”、“采用各种恰当的策略解决问题”、“检验和反思数学问题解决的过程。”[4]2010年，《美国州际共同核心数学课程标准（CCSSM）》提出的八项数学实践标准中，指出学生在数学问题解决的过程中，能分析条件、规划解决问题的途径、自我监控和评估、运用各种表征形式寻求关系和规律、并对结果进行检验[5]。德国2003年、2012年颁布的高中数学标准中，将“数学地解决问题能力”界定为学生“拥有恰当的数学策略去发现解决问题的思路或方法，并加以反思。”[6][7]丹麦学者尼斯（Niss）提出了八大数学能力，其中“数学地解决问题能力”被定义为“能解决别人或自己提出的各类数学问题（纯数学或者应用数学问题、开放或封闭问题），尽可能使用多种方法解决。”[8]我国课程标准中对于数学问题解决能力的界定关注学生运用数学知识解决实际问题、获得分析和解决问题的基本方法、体验解决问题方法的多样性、学会与他人合作交流以及形成评价与反思的意识。

 

　　综上，数学问题解决能力着重关注学生如何将情境中的问题表述成为数学问题，应用恰当的数学知识、方法和策略得到数学问题的解答，并能检验和反思问题解决的过程，同时注意在整个问题解决过程中，运用恰当合理的表征形式有效、流畅地表达整个思维过程。因此，本研究将“数学问题解决能力”从过程、结果、表达三个方面界定为“学生采用恰当的数学知识、方法与策略，解决在数学或其他情境中出现的问题，运用恰当合理的表征形式流畅地表达思维过程，并能检验与反思数学问题解决的过程。”

 

　　（二）数学问题解决能力的实证研究

 

　　如何对学生的数学问题解决能力进行评价？这是课程改革面临的一个重要课题，也是一个挑战。从大量的硕博论文中可以看出，以往有关数学问题解决能力的实证研究主要关注学生数学问题解决的过程、影响数学问题解决能力的心理因素（对问题的表征、思维水平、认知策略、对问题解决过程的监控）等。

 

　　在大规模的学生测评中，蔡金法等对中美六年级学生问题提出与问题解决能力的调查中发现，中国学生的解题正确率高于美国学生，同时中国学生倾向使用抽象策略和符号表征，美国学生则倾向使用具体策略和图示表征[9]；徐斌艳等对我国八年级学生核心能力进行测评时，关注学生问题解决过程中的识别信息、策略运用、数学表达、反思比较与评价，发现学生数学问题解决能力处于中等偏下水平，男生的问题解决能力显著优于女生[10]；曹一鸣等对八至十二年级学生的数学学科能力的调查中，发现学生在数学问题解决的过程中能用恰当的表征形式表征概念，能在简单的问题情景中识别并解决具体问题，能对结果的意义进行解释[11]。可见，大规模学生测评研究关注某一年级学生的问题解决能力表现，或者将数学问题解决能力作为数学核心能力的一部分进行了测试。而仅仅针对数学问题解决能力进行测试，关注不同年级学生发展的实证研究较少。

 

　　三、研究方法

 

　　（一）被试的选取

 

　　本研究采用分层抽样的方法在某地区五至八年级的学生中抽取被试样本。根据不同地理位置、不同经济发展水平选取了5所学校抽取不同的年级，并在选定的年级中随机抽取相应班级学生参加数学问题解决能力的测评。共有1734名学生参与，其中男生900人，女生834人；五至八年级的学生人数分别为499、379、449和407人。

 

　　（二）测试题的选择

 

　　数学问题解决能力测试题的选择考虑到以下两个方面的问题：第一，本研究的目标被试是五至八年级学生，测试题的难度既不能过于简单又不能过于复杂；第二，测试题要有一定的代表性并且能够被重复研究。通过咨询相关专家，确定了我国《课标（2011年版）》针对第二、三学段共有的“探索规律”部分作为测试内容，选取了被用于比较中、美学生数学问题解决能力差异的经典“圆点问题”和“铃声问题”[12]。运用SPSS 21.0对测试卷的信度进行检测，得到Cronbach’sα系数为0.782，信度较高。评分者两两评分后计算评分一致性系数，保证一致性在90%以上。

 

　　（三）本文的测评框架

 

　　表1 数学问题解决能力的测评框架     

 

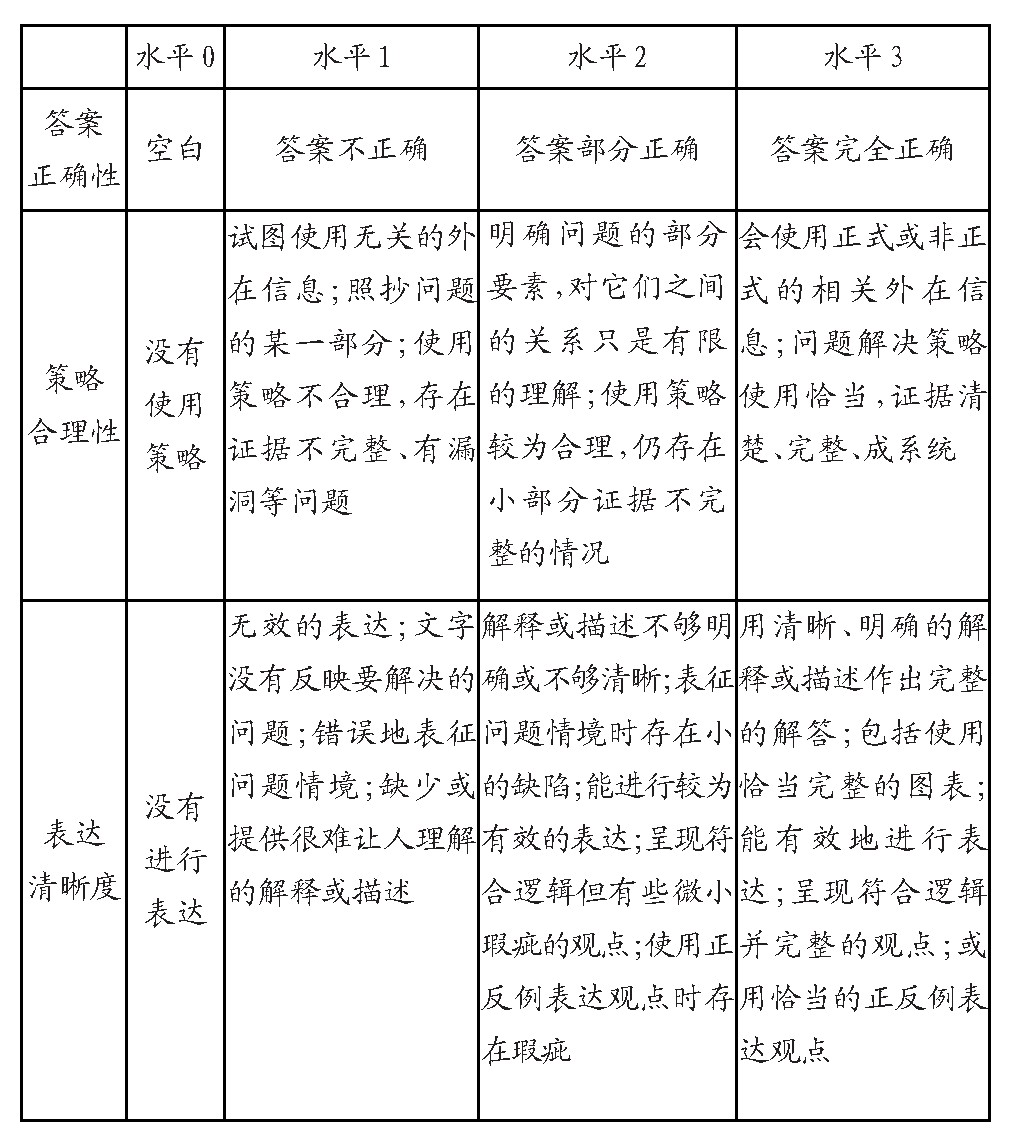
　　依据本文对于“数学问题解决能力”的界定，本研究从结果、过程、表达三个维度构建了问题解决能力的测评框架（如表1所示）。每个维度均有0-3四个水平，水平的划分标准借鉴参考了蔡金法等研究者[13]的相关研究。

 

　　三、五至八年级学生数学问题解决能力的具体表现

 

　　（一）学生数学问题解决能力存在“两极分化”现象

 

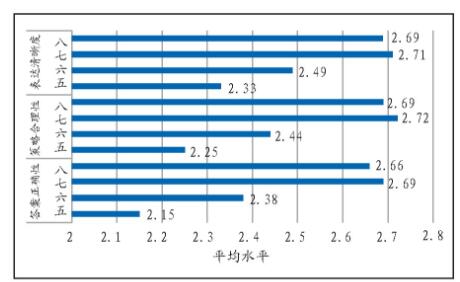
　　五至八年级学生在数学问题解决能力的三个维度“答案正确性”、“策略合理性”、“表达清晰度”上的平均水平如图1所示。

 

　

　　图1 各年级学生三个维度的平均水平   

 

　　显然，高年级（七、八年级）学生在数学问题解决能力三个维度的平均水平都高于低年级（五、六年级）学生。单因素方差分析邦费罗尼（Boferroni）检验结果显示，在0.05的显著性水平上，高年级学生的平均水平显著高于低年级学生。同时，五年级学生显著低于其他三个年级的学生。学生数学问题解决能力在低年级和高年级间存在“两极分化”现象，需要教师在六、七年级的过渡期充分重视。

 

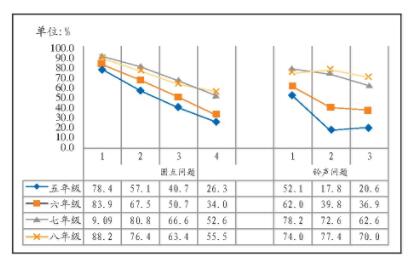
　　具体看数学问题解决能力的“答案正确性”维度出现的“两极分化”现象。各年级学生在“圆点问题”和“铃声问题”的各个小题能够完全做对（即“答案正确性”维度达到水平3）的人数比例如图2所示。随着每个小题难度的增加，各年级解答完全正确的学生比例也在逐渐下降，其中低年级学生出现了大幅度的“滑坡”。五至八年级学生“圆点问题”4道小题全部做对的比例分别为16.8%、21.6%、40.3%和42.5%，“铃声问题”3道小题全部做对的比例分别为12.0%、27.7%、53.9%和60.7%，做对所有7道小题的人数比例则分别为6.2%、13.5%、30.3%和34.4%。从问题解决得到最终正确结果的角度看，高年级学生的表现优于低年级的学生。

 

　

　　图2 各年级学生解答完全正确的人数比例   

 

　　（二）学生问题解决策略使用的倾向性与合理性水平存在差异

 

　　根据已有研究和学生在测试中使用的问题解决策略，本研究中总结出学生使用的三类策略：第一类，具体策略。学生运用列表、画图、先猜想后检验、枚举等方式得到最终的答案。第二类，半抽象策略。学生通过列出算式、逐步计算最终得到结论或者利用不完全归纳等方式发现规律得出答案。第三类，抽象策略。学生能在一般规律的基础上，通过列方程、写代数表达式等方式进行解答。

 

　　具体看各年级学生在问题解决策略使用上呈现出的特点，有如下两点发现。

 

　　1. 学生使用策略的倾向性与数学问题的抽象程度有关。

 

　　对抽象思维要求不高的问题，低年级的学生倾向使用具体策略，如“圆点问题”第2小题中，21.8%的五年级学生选择依据图形规律画出第6幅图，然后数出第6幅图中黑点的个数，六、七、八年级使用该策略的人数比例仅为5.8%、4.0%和3.4%；对抽象思维要求高的问题，高年级的学生倾向使用抽象策略，如“铃声问题”第2小题，要求学生总结出铃声次数与进入会场人数的规律，使用代数归纳策略的七、八年级学生的比例分别为74.6%和74.2%，而五、六年级学生的比例仅为20%和47%；“铃声问题”第3小题中，采用设未知数，列方程求解策略的七、八年级学生比例为45%和67.3%，而五、六年级仅为9%和21.1%。

 

　　题目难度适中时，低年级学生使用半抽象策略的人数比例较高，如“铃声问题”第3小题，五至八年级学生使用“通过人数和铃声之间的数量关系，列出算式，逆推铃声次数”这一半抽象策略的人数比例分别为29.1%、32.2%、23.6%和5.7%。

 

　　2. 低年级学生策略使用的合理性水平低于高年级学生。

 

　　本研究中，学生不合理地使用策略主要表现在：使用的策略不能被识别、部分或者错误地使用了枚举、算术、代数等策略。

 

　　五至八年级学生在“圆点问题”、“铃声问题”的7个小题中使用“不能被识别的策略”人次分别为985、559、423和426人次，占各自年级总人次的28.2%、21.1%、13.5%和15.0%，还有部分低年级学生直接用“猜”的策略，表现出较低的策略使用水平。

 

　　学生部分或错误使用枚举策略表现在“铃声问题”第1小题中，学生没有枚举到第10次铃声，少于或者多于10次，或者在枚举过程中计算出错；使用算术策略的不合理性表现在对算理的不恰当理解，如“圆点问题”的第4小题中学生用“44÷4=11（个），11-3=8（幅）”表明学生仅仅找到了白点个数增加的规律，并没有发现白点个数与图序之间的关系；不合理使用代数策略表现在“铃声问题”的第2小题，学生用n=2n+1,n×n+1等表达式来表示规律，并没有深刻理解铃声次数与人数之间的关系。出现以上不合理使用策略的学生绝大部分来自五、六年级。

 

　　（三）学生数学表达的表征形式与清晰度存在差异

 

　　根据已有研究和学生数学表达的具体表现，本研究总结出学生数学表达所使用的四种表征形式：文字表征，算术表征，代数表征，图示表征（包括图像和列表）来呈现数学问题解决的全过程，有如下两点发现。

 

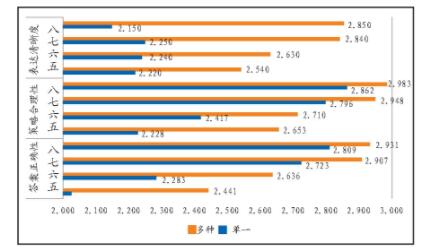
　　1.使用多种表征形式的学生其数学问题解决能力表现突出。以“铃声问题”为例，在数学问题解决的过程中，各年级使用一种表征形式和多种表征形式的学生其数学问题解决能力的相关情况如图3所示。

 

　

　　图3“铃声问题”中各年级使用不同表征形式学生的相关情况   

 

　　使用多种表征形式的学生在数学问题解决能力三个维度上的平均水平都高于使用单一表征形式的学生。T检验的结果显示，在0.05的显著性水平上，使用多种表征的学生与使用单一表征的学生其数学问题解决能力的三个维度水平存在显著性差异（p=0.000）。

 

　　2.使用不同表征形式的学生其表达清晰度存在差异。学生能用清晰、明确的解释或描述做出完整的解答是表达清晰度维度考量的重要依据。本次测评表明，低年级学生使用代数表征的表达清晰度不及高年级学生，但在使用算术表征时表达清晰度略高于高年级学生。具体表现为：

 

　　代数表征方面，“铃声问题”第2小题要求学生用公式或文字描述每次铃声响时进入会场的人数，高年级的学生会用诸如2n-1,n+(n+1)来表示第n次铃声响时，进入会场的人数，或者用函数表达式y=2x-1，其中x表示铃声响的次数，y表示进入会场的人数；而低年级学生则使用了大量错误的或者不完整的表述，如“2n+1”，“n=2n-1”，“前一次x，后一次x+2”，“n×n-1”等。使用代数表征的五至八年级学生的表达清晰度平均水平分别为2.320、2.618、2.702和2.805。单因素方差分析邦费罗尼（Boferroni）检验结果显示，在0.05的显著性水平上，五年级学生的表达清晰度显著低于其他三个年级。

 

　　算术表征方面，“铃声问题”第1小题中，多数低年级学生会仔细描述铃声次数与进入会场的人数之间的关系，或者尽可能用算术表达发现的规律，如“每响一次铃，进入会场的人数就比前一次多2人，因此第10次铃声响起时，进入会场的人数为1+2+2+……+2=19人”、“进入会场的人数是从1开始的奇数，因此1,3,5,7，……19人”，而高年级学生则会直接写出答案，或者简单的列出算式，没有将思维过程外显。在该小题中，低年级学生的表达清晰度平均值为2.490和2.511，略高于高年级的2.439和2.417，但单因素方差分析邦费罗尼（Boferroni）检验结果显示，在0.05的显著性水平上，低年级和高年级学生不存在显著性的差异。

 

　　四、讨论与建议

 

　　（一）重视学生数学问题解决能力的“两极分化”现象

 

　　五至八年级学生数学问题解决能力整体呈现上升的趋势，并且在数学问题解决能力的三个维度上，高年级学生的表现显著好于低年级的学生。六、七年级的学生出现了明显的“两极分化”现象，这符合学生身心发展、认知发展的一般规律。同时，低年级学生受自身数学思维发展的阶段性局限，在数学问题解决过程中，易使用不能被识别的策略，部分或者错误地使用策略；在选用代数表征形式进行数学表达时，低年级的学生也会出现表达不够清晰的现象。

 

　　低年级的学生（11-12岁左右）正处于皮亚杰认知发展理论中从具体运算阶段到形式运算阶段的过渡期，这个阶段也是学生从算术思维向代数思维转变的关键期，教师应当在学生数学问题解决能力的“分化阶段”，重视对学生问题解决能力的培养。莱斯特（Lester）总结出了好的数学问题解决者具有的五个特点：(1)数学知识紧密联系，具有丰富的图式；(2)关注问题的结构特征而非表面特征；(3)了解自身在数学问题解决方面的优势和劣势；(4)擅长监控和管理自身的努力；(5)考虑使用“优美（elegant）”的解法[14]。教师可以尝试教会学生在数学问题解决的不同阶段运用不同的知识，如在数学问题的转译阶段运用语言知识，在问题整合阶段使用图式知识，在解题计划和监控阶段使用策略知识，在解题执行阶段使用程序性知识等，分阶段、逐步培养与提升各个年级学生的数学问题解决能力。

 

　　（二）数学问题解决亟待高层次数学思维活动的参与

 

　　数学问题解决能力作为学生面对数学或其他情境中出现的问题时，运用恰当合理的表征形式流畅表达思维过程的集中体现，不仅需要学生记忆相关的数学知识、模仿相关的问题解决过程，更需要学生调动高层次的数学思维。

 

　　本次测评中部分学生出现随意猜测答案、机械使用解题策略、不恰当使用表征形式进行数学表达等现象均为学生进行低层次数学思维活动的集中体现。鲍建生指出，我国数学课堂教学自20世纪80年代以后，大多数所谓的问题解决沦落为低水平、知识贫乏的、工匠式的操作性活动。与此同时，数学问题解决能力的培养也逐渐退化为一些低层次的、以记忆为主的模仿活动[15]。《义务教育数学课程标准（2011年版）》指出“在教学活动中，要鼓励与提倡解决问题策略的多样化”、“引导学生通过与他人的交流选择合适的策略，丰富数学活动的经验，提高思维水平”[16]教师则需要设计高层次数学思维活动的问题和使用有效的针对高层次数学思维活动的教学策略，以调动学生的高层次数学思维，完成数学问题解决的全部流程。

 

　　（三）数学表达是学生数学核心素养外化的前提

 

　　数学问题解决能力是数学素养的重要组成部分，史宁中教授曾指出数学核心素养的本质是学生会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界[17]。本研究中，低年级的学生更愿意呈现整个问题解决的思维过程，尽可能用自己熟悉的数学语言表达自己的见解，而高年级的学生因为有一定的数学活动经验，能很快激活相关数学概念，则会直接跳过思维过程，直接写出数值、列出算式或者代数表达式，不加任何解释；同时，研究还发现使用多种表征形式的学生在数学问题解决能力的三个维度上显著高于单一表征的学生。杨向东教授指出学生核心素养的水平和学生在任务中的表现有时是不明确的，需要提供学生对表现或产品进行展示、论证或解释的机会[18]，学生在数学问题解决的过程中，通过清晰、明确、完整的数学表达才能真正将其数学素养外化，建议教师鼓励学生主动、清晰地进行数学表达，并尝试用多种表征形式展示整个问题解决过程。

 

　　（四）数学问题解决需要依托核心素养进行教学转型

 

　　我国《普通高中数学课程标准（2017年版）》提出了6大数学学科核心素养，这些核心素养的达成最终都指向学生数学问题解决能力的提升。面对纷繁复杂的现实问题，学生需要运用数学抽象的思维方式思考问题、逻辑推理的力量分析问题、构建模型的方式简化问题、直观想象的能力探索问题、数学运算的途径求解问题、数据分析的素养解释问题。

 

　　我国数学问题解决的教学在1980年以前，存在“重演练，轻应用；对题型，套解法”的现象，1980年以后出现了对“数学问题解决”理解片面的问题，如将其理解为“题海战术”，重视问题解决的最终结果，忽视学生思维过程等。郑毓信曾经指出，教师对于数学问题解决持有三种观点：第一，将问题解决看作一种教学手段，以达到复习、巩固及检查的目的；第二，将问题解决看作一种技能，使学生获得各种具体的解题方法和技巧；第三，将问题解决看作一种艺术，来进行创造性的活动[19]。数学问题解决能力的教学正在从传统的关注“双基”向培养学生思维形式和思维方法的创造性教学转型。教师可以在数学核心素养的教育背景下，借鉴集中指向学生数学问题解决能力培养的教学模式，如样例学习模式、认知学徒制模式、基于问题的学习模式（PBL）等，转变传统的数学知识传授、解题方法训练方式，提升学生的实践能力、创新意识，逐步认识数学的科学价值、应用价值、文化价值和审美价值。

 

　　参考文献

 

　　[1]核心素养研究课题组.中国学生发展核心素养[J].中国教育学刊，2016,(10):1-3.

　　[2]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京:北京师范大学出版社，2012.

　　[3]上海市青浦实验研究所，Qingpu Experiment Research Institute,Center for Teacher Development.关于教学目标因素分析的数据报告——以上海市青浦区数学学科为例[J].教育发展研究，2007,(7a):78-83.

　　[4]全美数学教师理事会.美国学校数学教育的原则和标准[M].蔡金法等译.北京:人民教育出版社，2004:50.

　　[5]全美州长协会和首席州立学校官员理事会.美国州际核心数学课程标准:历史、内容和实施[M].蔡金法等编译.北京:人民教育出版社，2016:16.

　　[6]徐斌艳.关于德国数学教育标准中的数学能力模型[J].课程.教材.教法，2007,(9):84-87.

　　[7]徐斌艳.德国高中数学教育标准的特点及启示[J].课程.教材.教法，2015,(5):122-127.

　　[8]Niss M. Mathematical competencies and the learning of mathematics:the danish KOM project[EB/OL].http://www.math.chalmers.se/Math/Grundutb/CTH/mve375/1112/docs/KOMkompetenser.pdf.2003.

　　[9]Cai J,Hwang S. Generalized and generative thinking in US and Chinese students’mathematical problem solving and problem posing[J]. Journal of Mathematical Behavior,2002,21(4):401-421.

　　[10]徐斌艳，朱雁，鲍建生等.我国八年级学生数学学科核心能力水平调查与分析[J].全球教育展望，2015,44(11):57-67.

　　[11]曹一鸣，刘晓婷，郭衎.数学学科能力及其表现研究[J].教育学报，2016,12(4):73-78.

　　[12]蔡金法.中美学生数学学习的系列实证研究[M].北京:教育科学出版社，2007:321

　　[13]Cai J, Jakabcsin M S, Lane S. Assessing Students’Mathematical Communication[J]. School Science&Mathematics,2015,96(5):238-246.

　　[14]Lester F K. Musings about Mathematical Problem-Solving Research:1970-1994[J]. Journal for Research in Mathematics Education,1994,25(6):660.

　　[15]鲍建生.关于数学能力的几点思考[J].人民教育，2014,(5):48-51.

　　[16] 中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京:北京师范大学出版社，2012.

　　[17]史宁中，林玉慈，陶剑，等.关于高中数学教育中的数学核心素养——史宁中教授访谈之七[J].课程.教材.教法，2017,(4):8-14.

　　[18]杨向东.核心素养测评的十大要点[J].人民教育，2017,(3):41-46.

　　[19]郑毓信.问题解决与数学教育[M].南京:江苏教育出版社，1994:35-38.