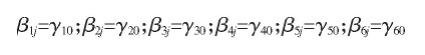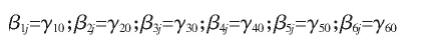八年级数学教学论文第五篇:八年级学生数学直观素养的表现与影响因素实证分析
摘要:基于湖南省Z市初中八年级学生的区域大规模数学学业监测,抽取Z市11个区县72所学校的20,446名八年级学生和297位初中数学教师为研究对象,对Z市学生的数学直观素养表现进行分析,并建立多层线性模型探讨影响学生直观素养的因素及其作用。测评结果显示:(1)不同群体、不同地域的学生数学直观素养存在一定程度的差异,留守生与非留守生之间的差异更为明显;(2)Z市初中生数学直观素养表现校间差异明显,其中,教师的直观教学方式以及学生的直观经验与信念、问题解决毅力、数学焦虑比可视化表征方式对学生数学直观素养表现影响较大。为此,不同群体学生数学直观素养的培育应有针对性,教师需注重直观教学引导,帮助学生克服认知偏见,关心留守学生的心理健康,帮其缓解数学焦虑。
关键词:初中生数学直观素养; 影响因素; 实证研究; 教育监测;
An Empirical Research and Enlightenment of Junior Middle School Students' Mathematical Intuitive Literacy——Based on the Monitoring of Mathematical Exercises of Z City of Hunan Province
Xu Zhuzhu
Abstract:Based on the regional large-scale mathematics monitoring data of the eighth-grade junior high school students in Z City of Hunan Province,20,446 eighth-grade students and 297 mathematics teachers from 72 junior high schools in 11 districts and counties of Z City were selected to pass the mathematical intuition of students.Performance analysis and the establishment of a multi-layer linear model to explore the factors that influence students' intuitive literacy. The evaluation results show that:(1)There are some differences in the mathematical intuitive literacy among students of different groups and different regions,and the difference between left-behind students and non-left-behind students is more obvious.(2)The mathematical intuitive literacy performance of junior high school students in Z City is obviously different between schools. Among those influencing factors,teachers' intuitive teaching methods,the students' intuitive experience and beliefs,problem-solving perseverance and mathematics anxiety have a greater impact on the intuitive literacy performance of the students than the visual representation. For this reason,the cultivation of mathematical intuitive literacy of different groups of students should be targeted,teachers should pay attention to intuitive teaching guidance,help students overcome cognitive prejudice,care about the mental health of left-behind students,and help them alleviate mathematical anxiety.
一、问题提出
数学一直是逻辑与直观的混合体,尽管目前形式逻辑占据主导,但任何数学活动都会经历由直观洞察到推理论证的思维历程。间接的逻辑形式往往造就了内部封闭的系统,反而感性的直观获得了许多直接永久的证据。直观虽有时使人陷入矛盾领域,被认为是不可靠的知识来源,但实际上直观却一直在数学教育中发挥着重要作用。数学史上,公理和逻辑只是搭建了数学的骨架,但直观给了它生命。[1]正是由于数学直观在科学演绎结构的发现以及问题解决的创造中所发挥的巨大作用,使得它最终成为一种重要的数学学科素养和核心能力,并且一直渗透在国内外数学课程改革的设计中。
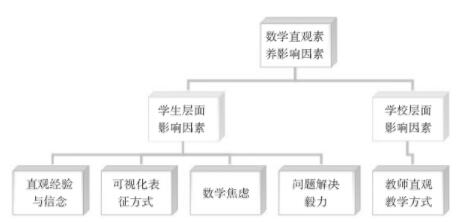
事实上,如何正确地评价学生的数学能力也一直是世界各国学者和数学教育工作者们长期进行探索和研究的课题。近年来,以PISA和TIMSS为代表的大型国际测评项目的兴起以及国内核心素养的提出,使得我国数学教育领域出现了不同规模和不同领域的数学学科素养或关键能力的测评研究。[2]但到目前为止,学界关于数学核心素养的界定仍不够统一和细致。数学直观作为数学学科素养和核心能力的重要组成,国内外文献研究、义务教育和高中数学课程标准虽都强调了数感、合情推理以及直观想象等数学直观领域,但却过于笼统,不能作为一套显性的、可测的测评框架。[3][4]因此,开发适合我国中学生特点的数学直观素养的测评体系显得尤为必要。那么,研究者首先需要界定数学直观的概念范围。广义上的数学直观素养涉及的领域则较为宽泛,既有对图形的感知,又蕴含思维的象征性。[5]并且,数学直观素养的形成过程又受到诸多层面的影响,其中影响的最大的因素主要包含直观经验与信念、可视化表征方式、教师的直观教学、数学焦虑以及问题解决毅力等方面[6](见图1)。
在本研究中,数学直观素养主要界定为个人在不同情境下依托各种基本数学直观形式解决
图1 数学直观素养影响因素
现实问题的能力,如数感、几何直观、空间想象和合情推理等关键能力的使用过程都会利用到各种数学直观形式。
总体上,目前数学测评研究仅仅集中在整个数学直观领域的表现水平,更多地侧重于直观素养与其他核心能力之间的联系和融合,很少触及数学直观的深层结构分析以及影响因素的制约作用。[7][8][9]因此,本研究借鉴国内外已有教育测评的经验,从直观情境[10]、认知水平[11]以及依托形式等方面构建数学直观素养测评模型,并综合考察不同层面(学生层面和学校层面)影响学生数学直观素养的重要因素[12]。
在本研究中,数学直观素养界定较为宽泛,主要基于PISA等代表性国际测评项目中数学能力的概念,并对已有数学直观研究文献进行梳理,从可操作性层面出发,把数学直观素养定义为个人在不同情境下依托各种数学直观形式解决特定内容领域问题的能力。这里的数学直观形式主要包括非图形直观形式和图形直观形式。其中,非图形直观形式是指借助相对具体、易被普遍接受的思维背景来进行直接感知与认识数学对象的直观形式;而图形直观形式是借助见到的或者想到的几何图形形象来直接感知与认识数学对象的直观形式。
本文最终以初中生数学直观素养状况和影响因素表现的测评为载体,着重解决如下问题:(1)初中生数学直观素养总体表现如何;(2)不同群体、不同地域的学生直观素养表现是否存在差异;(3)影响学校间学生数学直观素养表现差异的主要因素是什么,不同因素在多大程度上影响着数学直观素养。
二、研究方法
本研究主要采用标准测试法和问卷调查法。每个参与调查的学生需完成中学数学直观素养测试题以及影响因素问卷调查。问卷调查是为了考察不同层面影响学生数学直观表现的因素,研究者主要采用分层线性模型进行统计分析和数据处理。
1. 被试选择
本研究以湖南省Z市72所学校的20,446名八年级学生为被试,其中,男生10,634人,占总人数的52%,女生9812人,占总人数的48%;城市学生10,375人,占总人数的51%,县镇学生4946人,占总人数的24%,农村学生5125人,占总人数的25%。
2. 测试工具
测试工具包括:八年级数学直观素养测试卷、八年级学生问卷和中学教师问卷。
(1)数学直观素养测试卷
数学直观素养测试以《义务教育数学课程标准(2011年版)》为指导,借鉴国际数学学科大规模测试的经验,编制了考查学生数学直观素养的题本,涉及数与代数、图形与几何、统计与概率3大内容领域,能力水平要求覆盖了解水平、理解水平和应用水平。研究共选择考查学生数学直观素养的25道试题,分别来自A、B、S三套试卷,其中,A、B卷为预测试修改后组成的独立试卷,S卷是通过锚题设计1而组成的独立试卷(约一半来自A卷,一半来自B卷)。A卷总计12道试题、B卷总计13道试题、S卷总计14道试题。测试工具的题型分为单项选择题(四选一)和主观题,且主观题作答包括2~3问。三套试题整卷难度都在0.70左右,区分度介于0.27~0.69之间,其中区分度达到0.40(良好)以上的题目约占70%,内部一致性系数均大于0.89,信度良好。
(2)数学直观素养影响因素问卷
本研究根据文献梳理确定了影响数学直观素养表现的5大因素,并从学生层面和教师层面集中调查影响因素表现状况,由此项目组共设置了学生和教师两类问卷。学生问卷主要包括直观经验与信念、可视化表征方式、问题解决毅力以及数学焦虑4个分量表。其中,问题解决毅力和数学焦虑分量表源自PISA 2012学生问卷的改编,从“非常不同意”到“非常同意”,分别记1~5分,计算这些题项的均分,得分越高,表示程度越高;直观经验与信念、可视化表征方式为自编问卷,从“从不”到“频繁”,分别记1~5分,得分越高,表示频率越高。教师问卷主要涉及直观教学方式分量表,重点考察教师使用直观教学方式的频率,为李克特式五点自编量纲。
所有问卷题目都经过数学学科专家的修订,具有良好的信度,学生问卷和教师问卷的内部一致性系数分别为0.810和0.803,且两类问卷也都具有较好的结构效度(CFI=0.849,RMSEA=0.081;CFI=0.934,RMSEA=0.059)。
3. 测试程序
借鉴国际大规模测试的经验,数学学科团队先后经历了测试框架及细目表编制、题目收集及研磨、6人访谈、30人和300人预测试以及境内外学科专家和测评专家外审等环节,确保了整个测试流程的科学性和规范性。[13]
三、研究结果
表1 Z市八年级学生数学直观素养总体表现描述统计
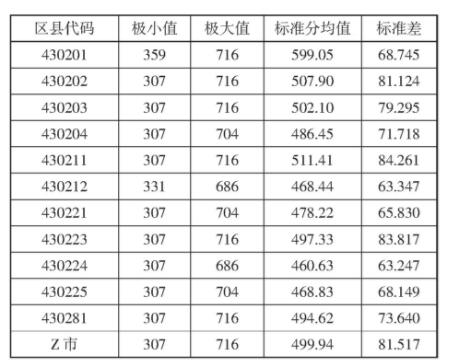
1. Z市初中生数学直观素养总体表现
(1)Z市八年级学生数学直观素养表现情况2
由表1可知,整个Z市只有430201区、430202区、430203区和430211区的学生数学直观素养表现高于全市平均水平,其他七区的表现都低于全市平均水平。另外,430212区、430224区和430225区学生数学直观素养整体表现较弱,但波动性较小;而430223区和430281区学生的表现和Z市平均水平最为接近。
(2)不同群体的学生数学直观素养表现的差异情况3
表2 不同群体学生数学直观素养表现
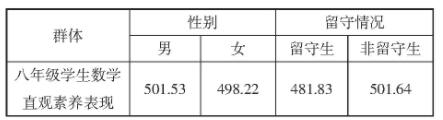
表2的独立样本t检验显示,Z市八年级学生数学直观素养表现存在一定性别差异(t=2.905,p<0.01,d=0.040),男生表现总体优于女生,但从统计功效上来看这种差异不具有实际意义。对于留守群体来说,留守与非留守学生数学直观素养表现存在显著差异(t=-10.205,p<0.01,d=0.249),尽管效应量较小,但留守学生总体表现要弱于非留守学生。
(3)不同地域的学生数学直观素养表现的差异情况
表3 不同地域学生数学直观素养表现
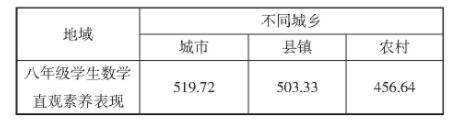
表3的单因素方差分析显示,Z市八年级学生数学直观素养表现存在显著地域差异(F=1148.676,p<0.001,ηp2=0.101),在统计意义上为中等效应。对于不同城乡的学生来说,但城市学生数学直观素养表现还是明显优于县镇,县镇学生数学直观素养表现优于农村。
2. 学生数学直观素养及影响因素模型分析
(1)学生层面数学直观素养影响因素表现
表4和表5分别给出了不同群体、不同地域的八年级学生数学直观素养的影响因素表现情况。
表4 不同群体学生数学直观素养影响因素表现
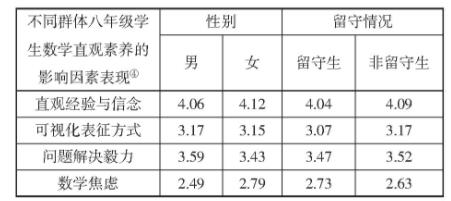
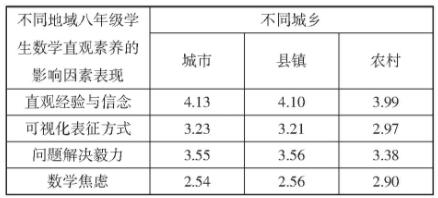
表5 不同地域学生数学直观素养影响因素表现
独立样本t检验结果表明,Z市八年级学生的直观经验与信念、问题解决毅力和数学焦虑存在性别差异,但可视化表征方式表现不存在性别差异(t=-4.873,p<0.01,d=0.073;t=13.078,p<0.01,d=0.190;t=-18.283,p<0.01,d=0.263;t=1.602,p>0.05,d=0.021)。虽然都是小效应,总体上女生还是比男生直观经验与信念更强,且数学学习更为焦虑,但男生数学问题解决毅力更强、更倾向于使用可视化表征方式;而对于留守群体来说,留守生与非留守生的直观经验与信念、可视化表征方式、问题解决毅力和数学焦虑都存在显著差异(t=-2.500,p<0.05,d=0.060;t=-4.002,p<0.01,d=0.108;t=-2.269,p<0.05,d=0.059;t=3.588,p<0.01,d=0.088),虽然效应量都较小,但留守学生总体表现为直观经验与信念不高、问题解决毅力不强,并且学习数学更为焦虑。
另外,由单因素方差分析可以发现,对于不同城乡结构的学生来说,城市、县镇和农村间的数学直观素养就各影响因素也存在一定地域差异(F=48.737,p<0.001,ηp2=0.005;F=127.480,p<0.001,ηp2=0.013;F=72.257,p<0.001,ηp2=0.008;F=169.533,p<0.001,ηp2=0.018),尽管效应量微弱,但城市和县镇学生还是比农村学生直观经验与信念更高、问题解决毅力更强,而且农村学生比城市和县镇学生数学焦虑感更高。
(2)学生数学学业成就及影响因素模型设定
以Z市八年级学生数学直观素养整体表现为因变量,以学生层(性别、留守、直观经验与信念、可视化表征方式、问题解决毅力及数学焦虑)和学校/教师层(地域、教师直观教学方式)为自变量,使用分层线性模型(hierarchical linear model,HLM)进行分析,测评结果详见表6。
(3)分层线性模型分析
零模型
第一层回归方程:Yij=β0j+rij;第二层回归方程:β0j=γ00+μ0j。
其中Yij是j学校的i学生的数学直观素养测试成绩,β0j为j学校的平均成绩,rij是学生个体的随机误差,表示j学校的i学生与学校平均成绩的差异;γ00为总体平均成绩,μ0j是学校的随机误差,表示j学校平均成绩与总体平均成绩的差异。
纳入背景变量(模型1)
在零模型学生层的基础上加入学生性别(男—女)和留守(是—否)变量,学校层加入地域(城市—县镇—农村)变量,以研究背景变量对学生数学直观素养的影响,模型为:
Yij=β0j+β1j(性别)+β2j(留守)+rij;
β0j=γ00+γ01(地域)+μ0j;β1j=γ10;β1j=γ20
考虑学生变量(模型2~模型6)
在模型1的学生层加入直观经验与信念、可视化表征方式、问题解决毅力及数学焦虑,以研究数学直观学生层面因素对数学直观素养的影响:
Yij=β0j+β1j(性别)+β2j(留守)+β3j(直观经验与信念)+β4j(可视化表征方式)+β5j(问题解决毅力)+β6j(数学焦虑)+rij;
β0j=γ00+γ01(地域)+μ0j;
考虑学校变量(模型7)
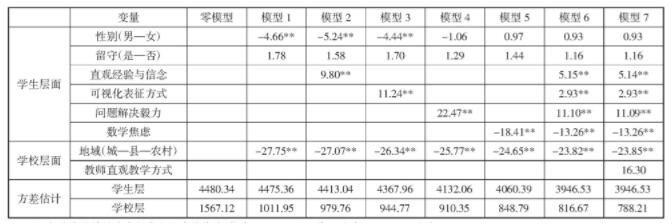
表6 八年级学生数学直观素养及影响因素HLM分析结果
注:方差估计结果为未标准化的残差估计,均在p<0.001上显著;*代表p<0.05,**代表p<0.01。
在模型6学校层的基础上加入直观教学方式,以研究学校层变量对学生数学直观素养的影响:
Yij=β0j+β1j(性别)+β2j(留守)+β3j(直观经验与信念)+β4j(可视化表征方式)+β5j(问题解决毅力)+β6j(数学焦虑)+rij;
β0j=γ00+γ01(地域)+γ02(直观教学方式)+μ0j;
零模型其实就是方差成分分析,通过计算跨级相关系数(ICC)可以发现,Z市八年级学生数学直观素养影响因素的零模型的ICC约为25.9%,这就说明造成Z市初中生数学直观素养表现差异有25.9%来自学校间的差异,即模型存在较大的组间差异,所以很有必要采用分层线性模型进行分析。
纳入背景变量后(模型1)可以发现,学生层变量(性别和留守)对学生的数学直观素养影响很小,此时,八年级数学直观素养的学生层解释率为0.6%;学校层变量(地域)对学校平均数学直观素养表现有很大影响(回归系数绝对值较大),并且其影响十分显著,这些和前文方差分析的结果也相互验证。
当考虑学生层变量时,在模型1的基础上(即控制性别和留守变量)分别纳入直观经验与信念、可视化表征方式、问题解决毅力和数学焦虑这4个变量,观察模型2到模型5可以发现,在加入问题解决毅力和数学焦虑时,学生层残差方差缩减较多,且观察模型6也可以看出,这两个变量的回归系数绝对值都比直观经验与信念以及可视化表征方式大许多。
当考虑学校变量时,在模型6的基础上纳入了直观教学方式这个变量,然后观察模型7可以发现,在加入直观教学方式时,学校层残差方差缩减较多,同时对比发现该变量的回归系数较大,直观教学方式整体上并不显著(p>0.05),但仍不可忽视教师直观教学方式对学生数学直观素养表现的影响。
总体而言,在学生层面,学生个体学习心理动力(直观经验与信念、问题解决毅力和数学焦虑)比数学直观学习方法(可视化表征方式)对学生的数学直观素养表现影响更大;而在学校层面,教师直观教学方式对学校平均数学直观素养表现的影响很大。
四、结果与讨论
1.八年级学生数学直观素养整体表现与学习心理存在群体差异
通过对调查地区学生的数学直观素养的测试结果进行分析发现,八年级学生数学直观素养的整体表现存在一定的群体差异。具体表现为:社会经济发展水平越高的地区,学生数学直观素养的整体表现相对越好;留守学生数学直观素养整体表现要弱于非留守学生许多;城市学生数学直观素养表现明显高于县镇学生,县镇学生的表现也好于农村学生;尽管学生数学直观素养表现不存在明显性别差异,但男生表现总体略高于女生。
上述结果也进一步说明,社会经济发展水平对学生的学业成就存在一定的正向促进作用。[14]经济发展水平越高的地方,学生的数学直观素养表现也更具优势。此外,男女生尽管在生理特征和学习心理上有所不同,但并没有造成两性数学直观素养表现出显著差异。相较而言,留守生与非留守生、城镇学生与农村学生之间数学直观素养的表现差距显著。面对具有明显教育优势的城镇学生,农村学生的数学直观素养整体表现往往处于不利地位。而作为社会转型期形成的特殊群体,留守学生的数学直观素养表现也不容乐观。通常留守学生受心理压力和学业焦虑等消极作用的影响,整体上的数学直观素养表现相对薄弱。
2.数学直观素养影响因素的预测作用明显
数学直观素养的生成离不开直观认知,而这一过程受到不同层面因素的影响,其中,学生层面涉及直观经验与信念、可视化表征方式、问题解决毅力和数学焦虑等因素,教师层面主要包括直观教学方式。为此,本研究通过分层线性模型综合考察了不同层面因素对数学直观素养表现的预测作用。数据分析的结果表明:在学生层面,直观经验与信念、可视化表征方式和问题解决毅力都能显著正向预测学生的数学直观素养表现,而数学焦虑则对学生数学直观素养表现出负向预测作用,并且问题解决毅力和数学焦虑的影响更大;而在学校层面,尽管直观教学方式对数学直观素养表现的正向预测作用并不显著,但不可忽视其重要影响。
实际上,已有文献也表明这些因素一直影响和制约着数学直观认知的形成和塑造。[15]个人累积的经验是直观认知的基本来源,并且由经验塑造成的稳定信念,最终促进数学直观素养的发展;随着学生问题解决毅力的持续增加,直观信念随之加强,数学直观认知也会更加稳固;可视化表征方式是获取数学直观性知识的重要来源,它会加速学生知识理解和直观认知的进程;与此同时,教师的直观教学引导也是促进学生形成直观思维并纠正直观偏见的重要力量;此外,数学焦虑等消极因素还会在直观认知的不同阶段阻碍数学问题解决,从而制约学生数学直观素养的表现。
五、启示与建议
1.关注不同群体学生的问题解决表现,有针对性地培养其数学直观素养
事实上,八年级正处于义务教育阶段承上启下的环节,不同群体学生对数学直观领域的知识掌握和问题解决过程都有所不同。从依托形式来看,男女生在非图形直观形式方面表现非常接近,而在图形直观形式方面,男生表现总体略高于女生,而留守学生表现总是弱于非留守学生。因此,在教学中教师应善于引导学生利用各种依托形式,如重视对类似“糖水变甜”等常识经验的联系[16]、借助变换等方式动态直观地刻画图形的属性,尤其还要关注女生几何直观能力的培养,如通过一次函数等内容的数形结合,有意识地培养其形象思维。
从情境维度来看,男女生在数学情境表现非常接近,而在生活情境和科学情境上,男生表现总体略高于女生,留守学生总体表现还是弱于非留守生,这说明女生和留守生都不擅长对问题情境进行迁移,故后续的数学教学应重点训练这两类学生在精细加工等方面的认知策略,帮助他们将新信息与已有知识联系起来,沟通日常生活与数学的联系。[17]
从认知水平来看,男生总体表现略高于女生,留守学生表现仍弱于非留守学生。其实,数学直观化过程也常常交织着逻辑理性,教师还应把对直观思维水平的认知调节作为培养数学直观素养的关键[18],如帮助学生识别物体或图形中几何特征、利用函数图像分析物体运动轨迹以及使用归纳、类比等方式探索图形或数字规律等。
2.注重数学直观教学指引,帮助学生克服认知偏见
无论是源于人类共同经历元素的几何或空间直观还是与自己生活各种领域相关的特别实践,它们在很大程度上都由经验所塑造,而直观的经验起源和作用也解释了学生长期存在的直观偏见。直观偏见一旦建立就异常强大,只有在教学中不断地引发学生认知冲突才能逐步更正错误观念、增加正确直观的信念。[19]教师的直观教学引导也是促进学生形成直观思维并纠正直观偏见的重要力量。
数学教学可以通过以下方式予以纠正:如引导学生在熟悉情境中把握数的相对大小关系、感受数的意义,初步建立数感和估算能力;鼓励学生利用生活和常识经验中的具体背景,并充分发挥思维直观的层次性;增强学生数学归纳和探索的积极性,使之成为一种稳定的心理习惯。此外,教师还可以借助图形或图像向学生进行直观、形象地讲解,鼓励学生使用可视化表征方式,让他们在图形或图表的视觉感知下自然地进行逻辑和理性思考,以加深他们对几何和空间的理解。
3.呵护留守学生的心理健康,引导他们缓解数学焦虑
本研究结果表明,对于留守学生来说,他们的数学焦虑感总是高于非留守学生。长期的学业焦虑,不仅影响他们对数学的态度和看法,不利于他们形成积极的自我概念,还会危害他们的心理健康。[20]此外,留守学生受心理压力和学业负担等消极作用的影响,问题解决的毅力不强,学习数学也更为紧张。[21]
为此,教师应对留守生群体投入更多的关爱,帮助他们正确估量自己的学习能力。在日常的教学活动中,班主任和生活教师需要经常与留守学生沟通交流,帮助他们减少孤独感和数学焦虑情绪,以增强学习动机和问题解决的毅力。[22]此外,我们还要增进学生的直观经验与信念,多鼓励学生使用可视化表征等方式进行学习。最后,学校和教师更应公平对待,避免在无意间做出伤害留守生自尊的不当行为,从而加剧留守的负面影响。
参考文献
[1]Richard L Tieszen, Mathematical Intuition.Phenomenology and Mathematical Knowledge[M].Dordrecht:Kluwer Academic Publishers,1989.
[2]张奠宙,鲍建生,徐斌艳.数学教育研究导引(二)[M].南京:江苏教育出版社,2013.
[3]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[4]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
[5]郭思乐.数学教学中的直观[J].课程·教材·教法,1986(5):40-42.
[6]Fischbein.Intuition in Science and Mathematics:an Educational Approach[M]. Dordrecht:D. Reidel Publishing Company,1987.
[7]杜佩璟.中学生几何直观能力研究[D].沈阳:辽宁师范大学,2009.
[8]徐德同,钱云祥.基于质量监测的初中学生直观想象发展状况的调查研究[J].数学教育学报,2017,26(1).
[9]宋思思.初中生几何直观能力的调查研究[D].上海:华东师范大学,2017.
[10]梅松竹.PISA 2012数学素养精熟度水平评价研究[J].教育测量与评价,2014(3):25-30.
[11]郝连明,吝孟蔚,黄迪.八年级学生图形与几何学习情况的区域质量监测[J].教育测量与评价,2015(7):30-34.
[12]Stacey K,Turner R. Assessing Mathematical Literacy[M].Berlin:Springer International Publishing,2015.
[13]路红,綦春霞.我国八年级学生数学运算能力实证研究[J].教育测量与评价,2018(2):54-59.
[14]程跟锁,李耀青,安雪慧.地方经济发展水平与学生学业发展关系研究[J].上海教育科研,2009(2):7-9.
[15]Fischbein,E.Intuition in Science and Mathematics[M].Springer Netherlands,2002.
[16]张广祥,张奠宙.代数教学中的模式直观[J].数学教育学报,2006(1):1-4.
[17]徐柱柱.东亚中学生数学学习策略及影响因素的性别差异研究[D].上海:华东师范大学,2016.
[18]Presmeg,N C.Prototypes,Metaphors,Metonymies and Imaginative Rationality in High School Mathematics[J].Educational Studies in Mathematics,1992,23(6):595-610.
[19]Wittmann E.The Complementary Roles of Intuitive and Reflective Thinking in Mathematics Teaching[J]. Educational Studies in Mathematics,1981,12(3):389-397.
[20]邢洋.初中生数学焦虑状况调查及相关因素分析[D].长春:东北师范大学,2009.
[21] 马艳琳,阳德华.对初中“留守儿童”学习习惯现状的调查研究[J].当代文化与教育研究,2007(3):83-85.
[22]崔丽娟.留守儿童心理发展及其影响因素研究[J].上海教育科研,2009(4):36-38.
注释
1两个不同的测验分别向不同的被试组施测,这两个测验中有一组相同的题目用来作为等值媒介,则这部分题目叫锚测验(anchortest,又译为铆测验);使用锚测验的设计,叫锚测验设计,又叫共同题设计。
2本研究采用IRT技术估算出学生的能力特质,并经过转化得到标准分(平均数为500,标准差为100),以此来代表学生的数学直观素养表现。
3文中的d、η2p分别代表t检验和方差分析的效应值。
4本研究以学生数学直观素养影响因素多个题项的平均值代表该维度的表现。
点击查看>>八年级数学教学论文(热门范文8篇)其他文章