八年级数学教学论文第七篇:前置作业在八年级数学课程教学中的应用实践
1 案例背景
在近几年的数学教学中笔者发现传统的数学作业存在许多弊端, 随着时代的发展, 这些弊端越来越制约着学生的成长和发展.数学作业的设计对于数学学习有着十分重要的意义.作业内容、作业形式、作业时间以及作业量的不同, 都会直接影响学生学习数学的兴趣和效果.因此, 完成数学作业是学生数学学习过程中不可或缺的重要环节, 学生完成数学作业的过程既是促进学习内容“理解-内化”的过程, 也是“巩固-掌握”的过程, 更是“拓展-应用”的过程.
2 案例描述
作为已有十五年教学生涯的老教师, 在还没进行课题研究之前, 笔者每一节课的流程基本上还是比较传统的:复习导入→讲授新课→学生练习→教师讲解.进行课题“数学‘前置作业’设计与运用研究”后, 笔者更注重“前置作业”的功效, 特别提倡课前请动个“小手术”——让前置作业起疗效.下面以《圆》的某一节课为例加以说明.
课题研究之前的教法:
(1) 直接讲授正多边形和圆里面的有关概念; (2) 讲解例题; (3) 学生做类似的练习; (4) 教师讲评, 巩固练习.
尽管讲解很详细, 教学层次很清晰, 但效果仍不太好.整节课都是教师在讲, 学生在听、在记, 学生基本处于被动接受的状态.久而久之, 学生就会失去学习的兴趣.教师应如何促进学生自主学习呢?教师要为学生提供自主学习的空间.学生要思考, 教师就得给学生思考的问题和时间, 这就需要教师提出问题, 让学生与学生之间、学生与教师之间进行探究互动, 通过探究互动来激励学生进行思考, 让学生去自主学习, 才能达到预期的教学效果.
下面是笔者进行课题研究后的教法.
2.1 让学生提前预习
这应该是教学方法的一个改革吧, 指导学生学法的目的就是最大限度地调动学生学习的积极性和主动性, 激发学生的思维, 帮助学生掌握学习方法, 培养学生学习能力, 为学生发挥自己的聪明才智提供和创造必要的条件.初中生往往不善于预习, 也不知道预习起什么作用, 所以笔者在自习指导学生预习的时候提出要求:
(1) 先粗略地把要学的内容自己看一遍;
(2) 细读:对概念要反复阅读理解, 注意知识的形成过程, 对不理解的概念、式子等做上记号, 以便带着问题去听课;
(3) 想想在预习中, 我懂得了什么.养成良好的预习习惯, 能充分提高学生的学习效率;
(4) 完成前置作业.
前置作业: (授课前一天自习课随堂完成)
(一) 复习巩固
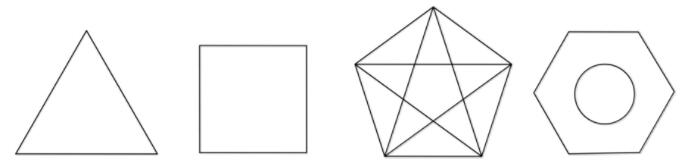
观察下列图形, 你能说出这些图形的特征吗?
图1
提问:1.等边三角形的边、角各有什么性质?
2.正方形的边、角各有什么性质?
3.等边三角形与正方形的边角性质有哪些共同点?
(二) 自主探究
1.观察生活中的一些图形, 归纳它们的共同特征, 引入正多边形的概念.
概念:______叫做正多边形.
(注:______相等与______相等必须同时成立)
2.提问:矩形是正多边形吗?为什么?
菱形是正多边形吗?为什么?
3.如果一个正多边形有n (n≥3) 条边, 就叫正______边形, 等边三角形有三条边叫正______角形, 正方形有四条边叫正______边形.
4.用量角器将一个圆n (n≥3) 等分, 依次连结各等分点所得的n边形是这个圆的内接正n边形;圆的内接正n边形将圆n等分.
5.正多边形的外接圆的圆心叫正多边形的______.
6.问题:正三角形、正方形、正五边形、正六边形、正八边形中, 哪些是轴对称图形?哪些是中心对称图形?哪些既是轴对称图形, 又是中心对称图形?如果是轴对称图形, 画出它的对称轴;如果是中心对称图形, 找出它的对称中心.
图2
问题:正多边形与圆有什么关系?什么是正多边形的中心?
发现:正三角形与正方形都有______和______, 并且为______.圆心就是正多边形的______.
分析:正三角形三个顶点把圆三等分;正方形的四个顶点把圆四等分.要将圆五等分, 把______等分点顺次连结, 可得正五边形.要将圆六等分呢?你知道为什么吗?
思考:任何一个正多边形既是轴对称图形, 又是中心对称图形吗?跟边数有何关系?
结论:正多边形都是轴对称图形, 一个正n边形有______条对称轴, 每条对称轴都通过正n边形的______ ;一个正多边形, 如果有偶数条边, 那么它既是______图形, 又是______图形.
7.用直尺和圆规作出正方形和正六边形.
8.如何作正八边形正三角形、正十二边形?
(三) 归纳总结:
1.______叫正多边形.
2.正多边形与圆的关系是______.
3.正多边形的对称性______.
(四) 自我尝试:
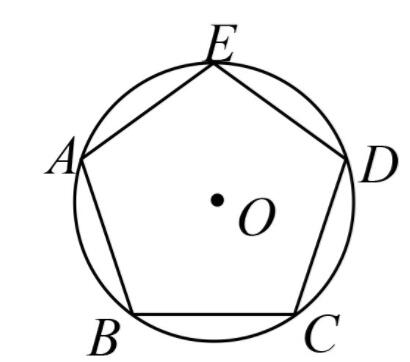
图3
1.已知:如图3, 五边形ABCDE内接于⊙O, AB=BC=CD=DE=EA, 求证:五边形ABCDE是正五边形.
2.各内角都相等的圆内接多边形是否为正多边形?
2.2 讲授新课
听课是学生获得知识的主要渠道, 教师在讲解之前可指导学生在听课的过程中注意: (1) 听清每节课的要求; (2) 听明白知识引入及其形成过程; (3) 听懂每节课的重点、难点以及老师对重、难点的剖析, 尤其是预习中的难点要在听课中弄明白; (4) 听懂例题解法的思路和数学思想方法的体现; (5) 听课后要做好小结.
授课过程如下:
(1) 提出问题:什么叫正多边形?必须符合哪两个条件才是正多边形?
(2) 讨论:正多边形是轴对称图形吗?是中心对称图形吗?我们能不能说正多边形既是轴对称图形, 又是中心对称图形?
经过讨论, 学生得出结论:所有的正多边形都是轴对称图形, 只有在边数为大于3的偶数时才既是轴对称图形又是中心对称图形.这些是学生经过讨论得出的, 这样会记得很牢.
(3) 在讲圆和正多边形的关系时, 设计了这样一个问题:正多边形的外接圆和内切圆有怎样的位置关系?我还没说完问题, 一个学生马上回答:两个圆是同心圆.我问真是这样吗?同学们不如同桌合作动手画画看.
(4) 以正六边形为例, 讲解正多边形外接圆半径、中心角、弦心距、边长之间的关系.
在没上这部分内容之前笔者听别的教师讲, 怎么得出中心角的度数很多学生弄不懂.在讲解的时候笔者主要引导学生从等分圆去理解, 学生不仅理解怎么得出中心角度数, 而且还自己总结得出中心角和外角的关系等等.
这样一节课就在设置问题、学生动脑动手中悄悄过去了, 本节课的教学已基本达到了教学目的.由此可见, 这样的教学设计使学生真正进行了自主探究学习, 发展了思维.
3 案例评价
在教育中, 马斯洛和罗杰斯提出了人本主义理论, 认为教育中必须以人为本, 以学生为主体, 真正地实现人性化教育.传统的教学方式下, 教与学依然属于“两张皮”, 教师讲的未必就是学生想学的, 未必就是学生不会的.多年教学实践发现, 一个学生要想取得优良的学习效果, 不仅教师的教要得法, 学生的学也要得法.长期以来, 教学多研究教师如何教, 少研究学生如何学.应时代发展的需求、教育改革的发展趋势, 培养具有终身自主学习能力的创新型人才势在必行.在义务教育初中阶段, 学生知识、能力、心理、思维等都处于急剧变化的关键期, 其自主学习能力的发展离不开教师的科学指导.对目前所在学校学生自主学习能力现状的调查显示, 随着年级增长, 学生自学学习能力总体呈现衰退趋势.实践证明, 忽视了学生学这个主体, 教很容易失去针对性、缺乏实效性.如果以“数学学习内容前置”为抓手, 通过对数学学习内容前置的深入研究, 做好初中数学课前学习设计, 不仅有助于学生预先学习所学的知识, 更有助于培养学生良好的学习习惯, 变传统意义上的被动学习为主动学习, 从根上改变教师的教学行为和学生的学习行为, 真正促进初中数学教学改革.
苏霍姆林斯基说过:“最好的教育就是自我的教育!”“前置作业”给学生提供了自由探索空间, 大多数经常预习的学生自学能力都更强, 学习也更主动、高效.笔者做的这样一种基于有效“预习活动”设计的实践尝试, 很好地培养了学生的学习兴趣, 增强了数学学习的主动性.经历了有效预习活动后, 学生学习的主动性提高了, 目的也更明确了, 注意力更集中了, 从而使课堂学习真正收到了良好的效果.
点击查看>>八年级数学教学论文(热门范文8篇)其他文章