第一篇初一数学小论文:
论文题目:如何引导初一学生发现和探索数学规律
[摘 要]学生升入初中之后,学习方法、学习态度都会发现很大的变化,学生与学生之间的差距更明显,因此,在数学教学中,需要探索数学规律,挖掘数学知识之间的内在联系,然后综合运用,这样,才能进一步提高学生的数学学习成绩。
[关键词]初一;数学规律;途径
数学规律就是指数学元素 (数与数、数与形、形与形等)之间的内在联系. 探索数学规律, 就是探索数学各个元素之间的相互联系. 布鲁纳说过:“探索是数学的生命线,没有探索便没有数学的发展. ”初一学生刚刚升入初中,对较复杂的数学规律往往一头雾水,如坠十里云雾之中,一脸迷茫,不知如何下手. 毛主席说:“入门既不难, 深造也是办得到的. ”那么,如何使学生入得其门呢? 关键是教师要引导学生如何透过现象看本质,如何找到探究问题的切入点,这才是至关重要的. 初一数学中 的 数 学 规 律 问 题 虽 说 千 变 万化,却万变不离其宗,还是有规律可循的. 事实上,探索数学规律就是对事物(数学元素之间)进行一般化的表示.
也就是如何对事物的内在联系从具体和特殊入手,经过观察 、类比、分析、归 纳 、猜想、验证的过程,再到抽象、一般的过程. 认识到“普遍性”寓于“特殊性”之中,也就是寻找藏在“个性”当中的 “共性”. 没有特殊性就没有普遍性. 人的认识过程往往要经历由特殊到一般,再由一般到特殊两个阶段,然后建立通式化的数学模型,这就要求教师要引导学生从观察问题入手,观察不同的数、形和前后左右的数、形之间有什么关联,经过分析比较,在头脑中有一个初步的猜想,再把它归纳概括和数学化,得出结论,然后验证结论的合理性,最后得出规律性的东西. 在这个过程中,观察是先导,切入是关键,发现是重点,也是难点,它是学生感性认识向理性认识的飞跃. 因此,在教学中,教师的作用就是引导学生从何处来切入,如何在山重水复无路之地找到柳暗花明的另一村.
从图形上观察、比较、猜想,发现数学规律
观察数学图形可通过对数学图形的结构进行分割, 寻找图形的上下、左右、内外等之间的某种联系,从而发现规律.例如, 观察直角三角形的内角和、锐角三角形的内角和、钝角三角形的内角和都是180°(特殊图形),从而猜想任意三角形(一般三角形)的内角和也是180°. 然后通过把任意一个三角形的三个角剪下来拼在一起去验证这个结论.
学生在实验当中不知道应该去观察图形的什么:是顶点,是三边关系,内角和, 外角和还是观察其他的什么. 此时教师就要引导他们从三角形的内角和去切入,去入手. 因为越是熟悉的东西,人们往往越熟视无睹. 然后, 可以引导学生再由浅入深、由表及里地去观察三角形的外角和,三边之间的关系,三角形的内心、外心、垂心、重心、旁心等,进一步由此及彼对四边形、五边形等进行观察、 分析、 归纳. 这正像一位哲人说的,“这世界并不缺少美,而是缺少发现美的眼睛. ” 因此, 教师要引导学生发现、探索数学规律的切入点. 事实上,自然界有很多规律并不难发现,而是难于不知从何处切入.
从数的特点去切入,去发现
数的前后左右上下内外之间有时乍看无规律可循,但经仔细观察,看它们之间是否有奇偶关系、 平方关系、立方关系、和差关系等,往往会灵机一动,灵感突至,有意想不到的收获. 因此,对初一的学生来说,教师在引导学生探索规律之前, 平时要多注重学生对偶数(2n)、奇数 (2n-1,2n+1)等 一些特殊数的表示的知识积累和铺垫,这样才能不至于有 “书到用时方恨少” 的感叹. 其次,教师还要引导和帮助学生分析给定的一列数是否是等差数列或等比数列.
再看分子、分母之间有什么关系,或分子与分子、分母与分母之间有什么关系,再进一步看它们之间和序号有没有平方、立方、和差关系、倍数关系,这样,复杂的问题也会变得轻而易举和得心应手.
通过列表,分析数据特点和联系
通过列表,把数据列出来,分析数据的特点(平方关系、立方关系等),再找出数据与序号之间存在着怎样的关系系 ,便可 探究 出这 一 类题 的规律 ,收到触类旁通的效果. 例如折纸、拉面问题等.
例3% 将一张长方形的纸对折,可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行. 连续对折6次后,可以得到几条折痕?想象一下,如果对折10次,有多少条折痕? 那么对折n次呢,会有多少条折痕?
分析 因为从第二次折叠起, 每一次折痕的条数等于在保留前面折痕的条数的基础上,再加上上一次新增的折痕条数的2倍,列表如表1.
表1
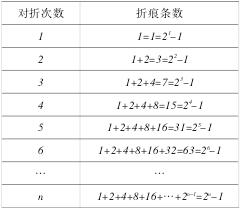
分析图形关系,培养探究能力对于图形问题,主 要 引导学生分析并寻找图形中的包含关系、对称关系 、倍 数 关 系 、递 增 关 系 、衍 生 关 系等,“快刀斩乱麻”, 透过现象发现规律,从而 培养 学 生 的观 察能力 、探 究能力.
例4% 图1中的图形是由边长为1的小正方形按照某种规律排列而成的.
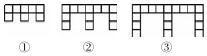
图1
观察图形,填写下表:
表2
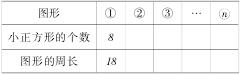
分析% 教师可引导学生观察这组图形中的任意一个是以中间这一列长方形(由小正方形构成)为对称轴的轴对称图形. 中间这一列长方形中小正方形的个数是序号加1, 即中间这一列有(n+1)个小正方形,中间这一列长方形的每一边(左、右)都有2n+1个小正方形,两边共有2(2n+1)个小正方形,因此图中小正方形的总数是(n+1)+2(2n+1)=5n+3. 而 图形的周长的计算方法则有多种. 这里只举一种:图形的周长等于横的正方形组成的这个长方形的周长加上三个竖的长方形(不包括已算过的横的长方形中的小正方形)的长的6倍.
图形中横排长方形的长为2n+3,三个竖排长方形的长为n, 因此图形的周长就等于(2n+3+1)×2+6n=10n+8.
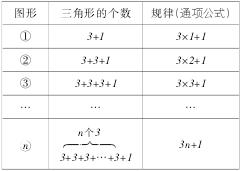
例5% 如图2, 图①中互不重叠的三角形共有4个; 图②中互不重叠的三角形共有7个, 图③中互不重叠的三角形共有10个,………则第n个图形中,互不重叠的三角形共有______个(用含n的代数式表示).
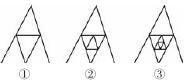
图2
分析% 在这个题中, 教师要引导学生观察并发现每一个图形中最里面的一个三角形, 在下一个图形中又包含(3+1)个三角形,这样不断衍生下去,我们就不难发现其中的规律:
表3
运用综合分析的方法,帮助和引导学生探究数学规律
在图形难以直观和一目了然的情况下,我们要帮助学生另辟蹊径,寻找探究数学规律的方法. 但这种综合分析的方法对学生思维的要求较高,学生不易掌握. 但一经掌握,便能左右逢源,使许多数学问题迎刃而解,这对学生来说获益匪浅.
总而言之,初一数学有关数学规律方面的问题林林总总、包罗万象,教师要引导学生探究数学规律,就必须首先帮助 和 引 导 学 生 寻 找 问 题 的 切 入点,这是探究数学规律的突破口. 其次,教师要鼓励和引导学生发展有条理的思考. 只有这样,才能使学生有的放矢,有章可循,便于学生发现和探究数学规律.





