2.3 图示法理解函数用幂级数逼近和用傅立叶级数逼近的区别。
学生常常不明白函数用幂级数逼近和用傅立叶级数逼近有什么区别,若单纯从理论上来分析解释,学生是难以接受和理解,利用 matlab 软件作图,可以帮助学生区分二者不同,化解难点。
我们可以利用前文中的 y=codx 的麦克劳林展式为例,帮助学生理解,函数的幂级数逼近只在某一点附近的逼近效果较好。对于函数的傅立叶级数逼近,我们可以采用下面的例子:g(x)是以 2π 为周期的周期函数,它在[-π,π]表达式为:
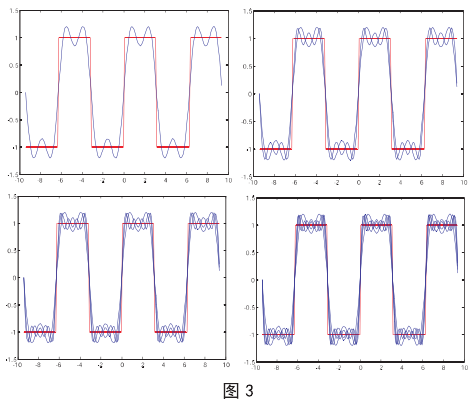
将 g(x)展开成傅立叶级数,并用 matlab 作图,分别比较 g(x)的傅立叶级数的前 3、5、7、9 项与 g(x)的接近情况。程序和图如下:
f='sign(sin(x))';
x=-3*pi:0.1:3*pi;
y1=eval(f);
plot(x,y1,'r’)
pause
hold on
for n=3:2:9
for k=1:n
bk=-2*(((-1)。^k)-1)/(k*pi);
s(k,:)=bk*sin(k*x);
end
s=sum(s);
plot(x,s)
pause
hold on
end
图 3 的四幅图中红色线为 g(x)的图形,是一方波,蓝色线为展开的 g(x)的傅立叶级数的不同项数的函数曲线,从图中可以看出,n 越大,整体逼近效果越好。通过 matlab 作图帮助学生理解了和函数的幂级数逼近只在某一点附近的逼近效果不同,函数的傅立叶级数逼近是整体的逼近。
【0
果越好。通过 matlab 作图帮助学生理解了和函数的幂级数逼近只在某一点附近的逼近效果不同,函数的傅立叶级数逼近是整体的逼近。
3 结束语
MATLAB 为多层次教学、演示教学、实践教学等现代化教学提供了一个良好的平台,通过 MAT-LAB 强大的符号计算功能和图像处理功能,调动了学生学习的积极性,起到了事半功倍的效果,真正体现了虚拟课堂的作用,为进一步提高教学水平和教学质量,推动高等数学教学改革提供了新的思路。
参考文献:
〔1〕吴磊。Matlab 在《高等数学》中的应用[J].阴 山学刊,2014,12.
〔2〕黄炜。MATLAB 在高等数学中的典型问题应用探索[J].江西科学,2010,2.
〔3〕张国辉。Matlab 在高等数学中的应用探析[J].当代教育理论与实践,2009,6.
〔4〕张栋恩,马玉兰,徐美萍,李双。Matlab 高等数学实验[M].北京:电子工业出版社,2006.







