
数学是自然科学研究和工程技术应用的重要工具,在理工科院校中,高等数学是一门非常重要的基础课,是学生学好其他基础课和专业课程学习的基础。然而,高等数学中涉及大量的计算,学生在掌握理论知识的基础上,要演算某个例题或者推算定义定理的时间较长。如果学生大部分时间都花在不必要的机械性的计算上,就会忽略对定义和定理的理解。Matlab 中包括大量的函数,直接调用这些函数可以方便实现高等数学中的极限、求导、积分、以及微分方程等计算问题。Matlab 指令表达式与数学、工程中常用的形式十分相似,学生稍加理解就能上手。在教学中引入 Matlab 提高了学生运用数学知识解决实际问题的能力。本文以同济大学数学系编着的《高等数学》为例,主要介绍符号计算和图形处理功能在高等数学教学中的应用。
1
符号计算在高等数学教学中的应用
1.1 求极限。
高等数学教学通常会介绍等价无穷小求极限、洛必达法则求极限、两个重要极限等方法求极限。
对理工科学生以及部分经济管理类学生在极限的应用中更关心的是所求极限的结果。这时学习一个Matlab 命令要比学习这些数学方法要快得多。
如求极限
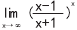
。此题用到的是两个重要极限求极限的方法,学生难于理解,而 matlab 命令为:
syms x
limit(((x-1)/(x+1))^x,x,inf)
回车即可返回结果:ans=exp(-2)
1.2 求积分。
高等数学求积分的内容涉及不定积分,定积分,重积分,以及积分的应用,但是在讲不定积分、定积分内容授课学时中 2/3 之二的时间都在介绍计算方法,包括凑微分、换元、分部积分、有理函数积分、反常积分。而 Matlab 的求积分命令只有一个却可以解决各类积分方法的积分求解问题。
如求积分
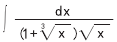
。 此题用到换元的方法求解,计算比较复杂,而 matlab 命令为:
syms x
int(1/((1+x^(1/3))*sqrt(x)))
回车即可返回结果 ans=6*x^ (1/6)-6*atan(x^(1/6))
1.3 求解微分方程。
高等数学微分方程这一章主要介绍微分方程求解方法,如齐次方程,一阶线性微分方程,可降阶的高阶微分方程,高阶线性微分方程,常系数齐次和非齐次线性微分方程。 对于具体的微分方程问题,学生往往不知道采用哪种方法去求解。Matlab微分方程求解也只有一个命令。
如求微分方程 y“=+y=xcos2x. 此方程为常系数非齐次线性微分方程,求解方法为先求得其所对应的齐次方程的通解,再求其一个特解。计算量较大,而一个。Matlab 命令就可以解这个微分方程,并且所有的微分方程求解都用这个命令。此题 Matlab 命令为:
dsolve(‘D2y+y=x*cos(2*x)','x’)
返回结果为:ans=sin (x)*C2+cos(x)*C1+4/9*sin(2*x)-1/3*x*cos(2*x)
2
绘图功能在高等数学教学中的应用
Matlab 强大的绘图功能可以帮助学生从直观上理解高等数学中抽象的概念,将逻辑思维与形象思维有机的结合起来。

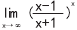 。此题用到的是两个重要极限求极限的方法,学生难于理解,而 matlab 命令为:
。此题用到的是两个重要极限求极限的方法,学生难于理解,而 matlab 命令为: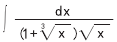 。 此题用到换元的方法求解,计算比较复杂,而 matlab 命令为:
。 此题用到换元的方法求解,计算比较复杂,而 matlab 命令为:




