
高等数学是一门重要基础课,它既是学习专业的后续课程与工程计算的工具,又是学生探索和创新的必备素养。然而由于它的内容的逻辑性强、抽象性高,并且内容多而课时少,再加上许多学生的基础普遍较差,而且水平差异大,因此该课程一直都被认为是老师觉得非常难教、学生觉得难学的课程。怎样提高教学质量和学生的学习效率,从而改善课堂教学效果,数学教师一直在不断地研究和探讨。在科学技术不断发展的新形势下,教育改革不断深入,高等数学已从传统的理论教学发展为注重它的实际应用性,将 Mathematica 软件用于辅助教学中,可以高效率的完成高等数学中的符号运算、公式演算、数值计算、函数作图等工作,强化代数几何的直观性,使得学生在观察数学现象的过程中不断地了解高等数学理论的基本思想和基本方法,从而对数学抽象概念的感性认识不断加深。
Mathematica 是由美国的 Wolfram Research 公司开发的一套软件,它是世界上应用非常广泛的进行数学计算和数学分析型的专业系统,具有简单易学的交互式操作方式,很好地结合了编程语言、数值和符号计算引擎、文本系统、图形系统、和与其他应用程序的高级连接。其在图形、数值、代数等方面应用广泛,它是世界上通用计算系统中最强大的系统,在数学、物理学、化学、生物、工程计算等许多领域都有广泛应用,自从 1988发布1.0 版本开始逐步更新改进,直到2016年3 月发布了10.4简体中文版本,功能更加完善,使用更加方便快捷。下面通过一些实例来介绍 Mathematica 软件在辅助教学中的应用。
1 Mathematica 解决极限的问题
所谓极限的思想,是指使用极限的概念分析和解决问题的一种数学的思想,极限思想方法是必不可少的一种高等数学的重要的方法,也是其与初等数学本质的区别之处。高等数学正是由于采用极限的思想方法才能解决许多初等数学无法解决的问题(如曲面体体积、曲边形面积、求瞬时速度等)。高等数学里的极限的概念非常抽象,学生在理解无限接近的数学思想时备感吃力,借助于 Mathematica 软件理解起来会更加容易。
计算函数极限的命令格式为:
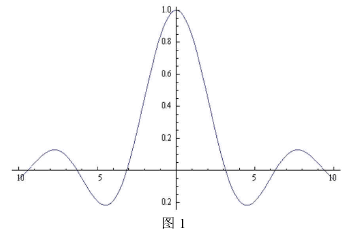
得到图像,通过观察函数的图像(图 1):
也可以看出来在无限接近 0 的过程中,函数会无限接近于常数 1,即以 1 为极限。对于用软件计算极限速度快而准确,让学生惊呼不已,大大提高了学生的学习兴趣,取得良好的教学效果。
2
Mathematica 在微积分中的应用
微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支,它推动了近代数学的发展,同时也推动了经济学、天文学、化学、物理学、工程学、生物学等自然科学、社会科学和应用科学的各个分支的发展。微积分中大量的习题都是非常复杂的,非数学专业学生大可不必花太多的时间去做,如求函数的导数,特别是学生计算容易出错的求复合函数的导数,用Mathematica 计算复杂函数的导数就非常简单。
例:求y =x^x*sin x 的导数和二阶导数。
Mathematica 软件的求导数的命令格式是D[f(x),x],求n阶导数的命令格式是D[f(x),{x,n}],通过在命令窗口分别输入D[x^x*sin[x],x]和D[x^x*sin[x],{x,2}]的求导命令运行就轻而易举地得到了正确结果x^x*Cos[x] +x^x(1 + Log[x])Sin[x]和 2x^x*Cos[x](1+Log[x])-x^x*Sin[x] +(x^(-1+x)+x^x(1+Log[x])^2)Sin[x].
定积分的求解主要命令也是用 Integrate.
只是要在命令中加入积分上下限 Integrate [f,{X,Xmin,Xmax}],也可以使用工具栏输入【1

例如:只
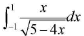
要输入 Integrate [x/√(5-4x) , {x,-1,1}],就能很快得出结果为1/6.学生掌握 Mathematica 软件大大缩短了抽象严谨的数学与学生认知水平之间的距离,可以减轻学生学习高等数学的学习负担,节省了大量的学习时间,掌握必需的高等数学知识,也为学习其他知识空出了大量时间。
3
Mathematica 用于几何作图
高等数学中的许多概念是需要靠图形来理解的,描绘函数的图像变得必不可少,函数的图像不仅能够体现出数学的美,也能直观地表示出许多重要的数学概念及函数性质。很多时候教师只是单纯地利用“描点法”作图既耗费大量的课堂时间,又只能做出粗略的函数的草图,缺乏图像精确性。甚至有些作图“描点法”是不可能实现的,这就要靠计算机,而这正是Mathematica 数学软件的强大功能,包括一维、二维、三维图形甚至动画。如讲完函数极值与最值的手工求法,马上就可以介绍计算机求法。例如需要绘制函数:sin(x*y)的三维图形就只需在命令窗口输入:
Plot3D[Sin[x*y],{x,0,3},{y,0,3}].
然后运行软件就得到图像(图 2):
应用 Mathematica 软件,只需要使用简单的命令就能轻松迅速地描绘出直观、准确的函数图形,而且能够运用动画的形式演示函数图像连续变化的过程,把抽象的数学式子与直观形象的图像有效联系起来,能够使学生对函数本质有更直观、更深刻的了解。
总之,传统高等数学课堂以教师为中心,学生的主动参与是有限的,引入 Mathematica 软件进行高等数学课程的辅助教学,解决了高等数学课程中教学缺乏直观性、概念抽象晦涩难懂的难题,给传统教学注入了活力,但是计算机计算也是一把“双刃剑”,过度依赖计算机计算,会使学生手动计算相对减少,久而久之会削弱学生的计算能力,在教学过程中,教师不但要强调学生牢固掌握高等数学中的基本概念和基本运算,也要培养学生利用计算机、利用 Mathematica 软件解决各类数学计算问题的应用能力,不断地强化学生的数学思想。只有把理论与实践很好地结合,才能更有利于改善学生的知识结构体系,提高学生的综合素质和能力。
参考文献:
[1] 王莱用。Mathematica 处理和分析实验数据[J].核电子学与探测技术,2000.20(2):142-144.
[2] 陈亮, 王显金。 Mathematica 软件在高等数学教学中的应用 [J]. 科教文汇,2007.12.
[3] 富成华,崔殿军。利用 Mathematica 数学软件实现高等数学教学的数形结合[J].辽宁师专学报,2007.12.
[4] 裘宗燕。Mathematica数学软件系统的应用及其程序设计[M].北京:北京大学出版社,1994.
[5] 顾培江。数学软件在高职数学教学中的应用[J].科技信息,2010.1.



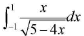 要输入 Integrate [x/√(5-4x) , {x,-1,1}],就能很快得出结果为1/6.学生掌握 Mathematica 软件大大缩短了抽象严谨的数学与学生认知水平之间的距离,可以减轻学生学习高等数学的学习负担,节省了大量的学习时间,掌握必需的高等数学知识,也为学习其他知识空出了大量时间。
要输入 Integrate [x/√(5-4x) , {x,-1,1}],就能很快得出结果为1/6.学生掌握 Mathematica 软件大大缩短了抽象严谨的数学与学生认知水平之间的距离,可以减轻学生学习高等数学的学习负担,节省了大量的学习时间,掌握必需的高等数学知识,也为学习其他知识空出了大量时间。





