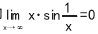2.1 图示法观察泰勒级数和原函数的逼近。
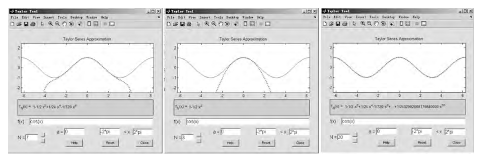
在教学过程中,很多学生对泰勒公式的含义理解不清楚,如果引入 Matlab 中的:taylortool 通过图形从直观上帮助学生加深对泰勒公式的理解,加深对泰勒级数逼近函数这一思想方法的理解。
如求 y=cosx 的麦克劳林展式。在命令窗口输入taylortool 回车,打开 taylor tool 窗口,函数 f(x)输入cos(x),a 输入 0,x 的变化范围输入 -2*pi,2*pi.分别给出 N=3,N=7,N=20 函数的逼近图形。 让学生理解,离 x=0 处越近函数的逼近效果越好,N 越大,函数逼近效果越好。
2.2 图示法理解振荡间断点和无穷小量与有界量乘积仍是无穷小量。
函数 y=sin(1/x)在 x=0 点处无定义,故 x=0 是间断点。但如何确定函数在该点的间断点类型呢?这时可以借助 matlab 绘图功能,帮助学生理解振荡间断点。
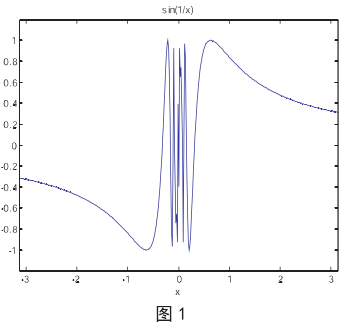
输入:ezplot(‘sin(1/x)',[-pi,pi]) 输出为图 1
输入:syms x
limit(sin(1/x),x,0)
输出:ans =-1 . . 1
从输出结果可以看出函数函数 y=sin(1/x)在 x 趋于 0 时,函数 y=sin(1/x)值在 -1 和 1 之间振荡,极限不存在,因此,x=0 称为振荡间断点。
先看一下函数 y=xsin(1/x)的图形:
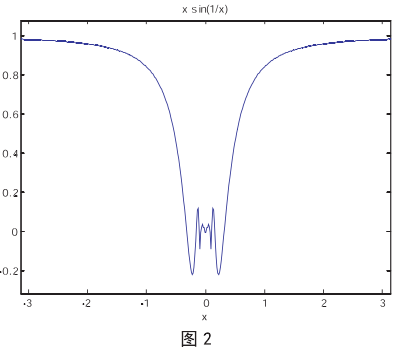
输入:ezplot(x*sin(1/x),[-pi,pi])
输出为图 2. 图 2 表明函数 y=xsin(1/x)的值不断振荡,但 |sin(1/x)|≤1,即 sin(1/x)在(-∞,+∞)之间是一个有界的函数,并且在 x 趋于 0 时,函数 y=xsin(1/x)图形离 0 的值越来越近,即趋近于 0.
再求函数在 x 趋于 0 时的极限:
输入:syms x
limit(x*sin(1/x),x,0)
输出: ans=0
即
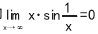
通过函数 y=xsin(1/x)。
的图形和极限可以帮助学生理解无穷小量与有界量的乘积仍为无穷小量。