科学阐释逻辑在知识研究中的重要作用

　　知识是智能行为的核心,以显性形式体现的获取知识、知识加工以及利用知识进行交流的能力,是人和其它动物的区别。任何对智能行为的研究,无论是理论上的或者是经验上的,都有一个共同的出发点,即知识科学,主要研究知识的基本形式以及如何获取和处理知识。而逻辑是处理知识科学的重要的工具。

　　知识在日常生活中发挥着非常重要的作用。事实上,每个人的行为都基于自己的知识。关于知识问题的思考已经由来己久,古希腊的哲学家就曾经问道:“我们究竟能够知道什么?”“说一个人知道什么的意思是什么?”这属于认识论的范畴,主要研究知识的不同定义、知识的基本形式属性、外在主义和内在主义观点之间的争论,同时还面临着怀疑论者的挑战。柏拉图将知识定义为“正当性得到证明的真信念”,欣迪卡则认为知识是“在可能性的逻辑空间中为真”,欣迪卡的主要目的在于用形式化的方法研究知识的本质属性。德雷特斯克则将知识定义为“由可靠的相互关联所支持的信念”等,但关于知识尚无统一的认识。知识的稳定性不只是作为单个主体或单个命题的孤立的特征,而应该在包括更多的认知态度、认知主体和丰富的认知行动的指令框架中进行解释,知识的稳定性在于它能够在复杂的认知环境中成功地得到运作。逻辑往往可以看作是通往知识的一座桥梁,同时也突显了逻辑的重要作用。知识科学包括自然科学和社会科学,如物理、化学、计算机科学等。下面就针对这些具体的知识科学阐释逻辑在知识研究中的重要作用。

　　19世纪的逻辑学家们所研究的归纳推理部分地涉及到经验科学,可将其视为知识科学。但是,在20世纪末,逻辑发展成为数学的特殊分枝,即逻辑的数学转向。

　　20世纪中期为“逻辑的黄金时期”:弗雷格(Gottlob Frege)在1893年的《概念文字》中发展了谓词逻辑;罗素 (Russell)和 怀 特 海(Whitehead)在1910年至1913年出版了他们的三卷本的《数学原理》,以逻辑的方法重建了纯数学的基础;而哥德尔(Kurt Godel)证明了任意一个包括自然数在内的逻辑系统都是必然地不完全的(即,允许真值形式的逻辑系统在系统内是不可证明的)。这严重地打击了逻辑学家们的积极性。尽管如此,仍然不能阻止逻辑学家们前进的步伐,随后逻辑学家丘奇(Alonzo Church)发展了更有表达力的逻辑系统(例如组合逻辑和高阶逻辑),塔斯基(Alfred Tarski)构造了最重要的现代逻辑,即独立的语义理论。希尔伯特证明了协调性,主要是受数学的影响。拉姆齐描述了理论的作用,特别是经验理论,主要是从语义学角度进行的研究。普谢温茨基对科学理论的形式语义学方面的研究做出了巨大的贡献。而斯尼德运用形式化机制对经典量子力学进行了分析。早期的逻辑论题和一般科学方法论是紧密结合在一起的,包括穆勒、皮尔士、塔斯基、卡尔纳普、欣迪卡等。同时,逻辑和科学哲学之间也存在着密切的关系,当今逻辑也关注信息的一般结构和推理的多主体行为等论题。

　　一、逻辑

　　语义和语形之间的关系是逻辑、语言和计算机科学研究的核心。逻辑主要是对推理的研究,故逻辑学家既要研究推理行为也要研究推理结果,既研究推理的规范也研究对规范的刻画,既研究推理的归纳论证,也研究推理的演绎论证。

　　逻辑学既与哲学、数学以及语言学关系密切,也与心理学、法学相互促进。逻辑对于科学理论的研究主要表现在以下几个方面。

　　(1)句法。埃因霍温的自动数学理论可应用于数学的实际计算机形式化中。(2)结构。在量子力学的逻辑研究中,运用到了希尔伯特空间“隐藏的变元”的结果。阿什比在讨论有穷机器时就用到了句法理论,得出“相互同态的力是同构的”结果。(3)语义学。语义学在几何学、语言学和机械“决定论”领域中都具有重要的作用。(4)语用学。欣迪卡的“博弈论语义学”具有广泛的用途。

　　在数学和计算机程序中发挥着重要作用的语义关系是一种逻辑等价关系,在语形运算中试图随意删除或者增加语义是不可能的。例如,逻辑定理的等价描述(例如“不存在最大的素数”和“存在有无穷多的素数”)实质上都可以看作是同一个定理,此时更看重的是推演或者逻辑蕴涵。两个表达式是逻辑等价的,当且仅当每一个表达式都可以推出另一个表达式。语形转换是弱蕴涵表达式,称为可靠的转换,但逻辑学家们更关注语形转换的完备集,运用这种形式可以生成所有可能的蕴涵表达式。

　　可靠性和完全性是评价数理逻辑优劣的标准,转换或者推理规则,也是计算机科学中的许多领域研究的重点。同时数学公理、语法或者特殊程序,在抽象层面上是完全的。在数学中的推理形式只能是可靠的推理或者演绎。

　　二、非演绎推理形式

　　在经验科学中,绝大多数推理都不是演绎的。通过观察而得到的推理理论通常不可能是可靠的,而严格地说结论可能是或然的。所以放弃可靠性或许会使推理变得更有用,但这样就无法保证结论是必然真的。

　　事实上,非演绎推理是普遍存在的,在大多数情况下,非演绎推理时常是正确的。可见,不可靠推理具有一定的作用,推理中对不正确的推理和(例如在观察到10只白天鹅之后得出所有的天鹅都是黑色的)不可靠但可能是正确的推理(例如经过同样的观察推出所有天鹅都是白色的)进行区分。

　　在不可靠推理中存在有不同的形式:对于缺少前提的推理,可利用假设分析的方法,通过观察概括出结论;另一种是对特殊对象的观察行为做出解释。概率是对不可靠推理的可靠性进行预测以确定其观察所依赖的基础的重要方法。

　　可以对哪些不可靠推理进行有意义的区分?如何根据演绎对每一个不可靠推理进行区分?对于任意的演绎推理,都可以区分出必要条件和充分条件吗?归纳可靠性和演绎可靠性有哪些区别?这些问题是大多数逻辑学家所关心的中心论题。

　　在逻辑发展过程中,推理的主要形式究竟是哪一个?其主要特征是什么?通俗地说,推理处理的是形式论证,即从前提推出结论。根据前提和可接受的结论之间的关系,可以得到不同的推理形式。例如,如果增加新的知识之后,结论仍然是有效的,那么该论证就是演绎的。如果只允许演绎论证,那么该推理形式就是演绎的,演绎推理是不可废止的(non-defeasible)。逻辑系统是特殊的形式化的推理形式。

　　逻辑的形式化有许多特殊的推理形式:例如,模态逻辑、时态逻辑、相干逻辑和直觉主义逻辑,其中每一种形式化都是一个确定的演绎推理。这些演绎逻辑并不能必然地确定哪一个论证是演绎有效的,哪一个论证不是演绎有效的。

　　另一方面,非演绎推理形式是可废止的:尽管作为结论根据的前提不能被驳倒,但结论却可能被新增的知识所驳倒。例如,论证“鸟通常会飞;X是鸟;因此X会飞”是非演绎的,因为X可能是一个企鹅。论证“在一生中每天太阳都升起;我确实不知道太阳在最后的某一天没有升起;因此,太阳将在未来的每一天都升起”不是演绎的,因为如果太阳明天没有升起,结论就是无效的,但前提却是真的。关于X的论证称为似然推理(plausible reasoning):关于一般情况和异常情况的推理。似然推理包含演绎推理:如果知道X是一个普通的鸟,该论证将是演绎有效的。这种似然推理称为“超演绎的”(supra-deductive),或者称之为准演绎的(quasi-deduc-tive)。另外一个准演绎推理就是反事实推理,或“假设分析”(what-if),即以虚假前提为开始。例如,论证“如果你在早晨不叫醒我,我将确信会错过晨练”是一个反事实论证,因为前提和结论在预期的解释中都是假的。如果确定环境条件已经发生了变化,这样的论证用来说明将会发生什么样的变化。

　　另外还有称为“非演绎的”(a-deductive)的推理形式。上面的“太阳升起”的例子属于归纳推理,非演绎的推理形式就是将特殊的观察(也称为证据)概括为一般的规则或者假说(hypotheses),要求前提和可接受的结论之间具有形式化定义的推理关系,这一点和演绎中的衍推相类似。

　　非演绎推理形式还包括溯因推理(abduction),该概念是由皮尔士(C.S.Peirce)提出来的,表示把某些证据作为解释性的前提(即前提可从证据推演出来)。例如,“所有从袋子中取出来的豆都是白色的;这些豆是白色的;因此,这些豆是从该袋中取出来的”是一个溯因推理。近年来,溯因推理在逻辑程序研究领域比较流行,表示已经知道了一般的解释之后,但并不能确定其前提是否是真的;溯因推理则可看作是前提缺失的假设分析。溯因推理和归纳推理可以相互补充:在特殊的情况下,如果已知前提和结论都成立,利用归纳推理可以推出一般的规则;而已知一般的规则和特殊结论,以及它的某些前提,溯因推理可推出特殊的前提。另外,在溯因推理和似然推理之间也存在有很强的关系:溯因推理可以回答“如果希望推出鸟会飞,就需要假设鸟X是一只普通的鸟”。

　　以上对推理的分类形式可用图1表示。

　　【图1】

　　三、似然推理

　　非单调推理也称“似然推理”。单调性指随着前提集的增加(或减少),结论集也随着相应的增加(或减少)。换言之,单调性就是指如果在已知前提中增加一个新前提,那么结论仍然是有效的,该性质也称为不可废止性。任意非演绎推理形式都是可废止的,故任意非演绎推理形式都是非单调的。非演绎推理形式中的非单调性在使用时需要进行某种限制,例如缺省推理(default reasoning)。

　　似然推理是“根据已知信息所进行的推理比演绎推理更优越”,比演绎推理更自由或者更可信。相应地,根据似然推理主体可接受的论证集(也称为推理关系consequence rela-tion,可定义为L×L的子集,其中L为语言)可以分成演绎部分和似然部分。演绎部分对应的论证不包括某些特殊规则。

　　似然推理中的非单调推理类似于:从鸟可以推出会飞,但从鸟和企鹅就不能推出会飞。Kraus等人提出,通过允许例外的规则,除了单调性规则外,演绎推理还有其它性质。

　　一般地,命题演绎推理可以通过下面的规则刻画:

　　

　　在这些规则中,对应于有背景知识的隐性主体,αβ表示推理者存疑地接受从α到β的推理。另一方面, 表示经典演绎推理(关于同样的背景知识)。可以对这些规则进行组合:例如,根据自返性和右弱性,每当α γ蕴涵α γ,即后承关系 是超经典的(supra-classical)。

　　Krau等人证明上面五条规则刻画了演绎推理。存在等价规则集:例如,切割可以用下面的右并且进行替换,左或者可用右蕴涵替换。

　

　　这两条规则显然都是通过单调性———谨慎单调性推出的,特别地,利用似然推理,使前提得到了增强,这种似然推理可称为偏好(preferential)推理,因为可以通过假设状态间的偏好序来模型语义,其中的状态为模型集,且规定αβ当且仅当每一个最大偏好状态满足α同时也满足β(一个状态满足一个公式当且仅当它的所有模型满足该公式)。通过减弱偏序状态之间的偏好关系条件使得偏好推理变得更弱;这使得左或者规则无效,但其它的规则不变,该种推理称为累积(cumulative)推理。切割和谨慎单调性可推出:如果αβ,那么α γ,当且仅当,α∧βγ,即似然推理可以在前提中得到累积。

　　据前可推出演绎推理者是有偏好的(对应于空偏好关系),偏好推理者是可累加的。通过对推理形式X和Y进行对比。如果可以构造,对每一X推理者,满足规则Y的论证的唯一最大子集,这样就可以将偏好推理归约(reduction)为演绎推理。反之,单调性(如果γ α且γ/β,那么α/β)论证不是演绎判断。

　　许多逻辑学家经过论证,得出逻辑是必然单调的,非单调性逻辑显然是矛盾的。但是,基于数学推理性质的单调性和逻辑的单调性之间是有区别的。

　　Kraus等人利用演绎的元逻辑的推理关系对多种形式的非演绎推理进行了形式化。

　　例如谨慎单调性规则事实上是合理性假设(rationality postu-lates),需要被任意理性推理的主体类所满足。这一点至关重要,他们构造的方法也可以作为分析其它形式推理的方法。

　　四、归纳和溯因推理

　　归纳是将特殊证据概括为一般规则的过程。简单的归纳形式就是从样本到总体的推理:观察到Fs中有百分之Y是Gs;因此,(近似地)所有的Fs的百分之Y是Gs。

　　该论证模式和下面的推理非常类似:所有的观察Fs是Gs;因此,所有Fs是Gs。

　　该归纳规则不需要利用实质蕴涵:样本中所有对象都满足P(y);因此,总体中所有对象都满足P(y)。

　　这些归纳生成的公式存在有关键性的问题:通常地,在一般规则中所使用的谓词P并没有在观察中显性地给出。

　　下面谈谈假设概括(hypothesis generation)。

　　在科学哲学中,经常忽略假设概括。例如,在《猜想与反驳》(Conjectures and Refutations)一文中详细地描述了这样一种情况:希望验证猜想,但却无法回答在猜想开始的第一步是如何提出的。另外,如果希望主动地进行科学发现或者学习(在人工智能的子领域中称为对机器学习的对象的研究),必须利用假设概括这条规则。假设概括并不是完全非理性的,且该问题转化为:理性假设对什么样的归纳进行限制才能假设概括呢?

　　事实上,美国哲学家Charles Sanders Peirce在1903年已经考虑到该问题。其推理的形式如下。观察到了奇怪事情C:但是如果A是真的,C将当然是真的,因此,根据似然推理有:A是真的。

　　这样,对A并不能进行溯因推理“如果A是真的,C理所当然是真的”[5]57。

　　Peirce称该假设概括的过程是溯因推理(abduction),并将溯因推理定义为“解释假设的形式化过程”,即“溯因推理纯属于构造某些可能的事实”。

　　现在的“溯因推理”具有多层含义,在哲学上,已经习惯上将溯因推理看作“关于最佳解释的推理”。在人工智能领域中,溯因推理通常被视为从结果到原因的推理,或者从证据到解释的推理,但并没有做出概括。另一方面,归纳的目的是在个体进行观察之后再做出概括。而在归纳论证模式中,同样并未用原因来解释结果。

　　Peirce认为溯因假设概括的逻辑形式可以简化为“从C,A C,溯因A”或者,引入符号 表示溯因推理,“如果AC,那么C A”。利用Kraus等人的后承关系方法来对理性假说进行形式化表示假设概括。首先给一般的规则:

　　

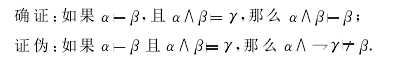
　　确证和证伪指如果β是可能的前提,已知观察α和γ是建立在β(和α)上的预测,那么β无法通过观察γ为真的规则得到确证,但可以通过观察γ是假的得到证伪。

　　五、证实的归纳

　　前面的公理集主要关注的是归纳以及基于解释推理的溯因,还有就是推理假说,可以通过观察加以证实。该观点是由亨普尔(Carl G.Hempel)最先提出,并给出推理的公理集(或者称为充分条件)和证实的实质定义。

　　下面是亨普尔给出的充分条件,主要是对元语言进行了形式化的处理:

　　

　　这些公理是合理的,如果证据太弱无法将不相容的公理排除———换言之,需要把观察看作是完全性公理。

　　亨普尔对充分条件进行形式化处理的主要原因是为了验证确证的实质定义,但并不能保证它们在任何含义下都是完全的。下面的理性公理集表示确证归纳相对于恰当的语义设计是完全的。

　

　　如前,不允许矛盾观察(和亨普尔的不同)———一个弱衍推形式可以从预测右弱化推出,且将弱自返性变为独立规则,同时增加了两个新的规则。验证(verification)指将预测γ增加到证实观察α中推出前提β,强证实指的是任意γ都可被α所确证。右并,其基础假定是观察完全足以使所有的“在同向上的点”得到确证。左或可以看作是在解释推理中所讨论的对左弱化的一个变形。而左弱化指在确证情况下无效。左或是通过单独观察确证前提可以通过对析取进行弱化推出。

　　和公理相对应的语义是可证完全的,该语义是由Kraus等人通过对似然推理的偏好语义的变形得到的。事实上,关于确证归纳公理和在3部分中所考虑的公理具有紧密的联系:例如,强证实和谨慎单调性完全等价。

　　不足之处在于,如果将右弱化和右增加进行组合将会导致该系统的坍塌,即任意的观察都可以证实任意的假设。解释假设却可以进行任意增加,但并不必进行弱化;证实假设可以任意地弱化,但仅在确定条件下得到增强。为了证实假设概括的公式,使假设都得到解释,并且能通过观察得到证实。解释和证实归纳之间的区别涉及到证实悖论。

　　六、结论

　　逻辑学有特定的学科范围吗?至少可从两个方面来思考:一是方法论的,即逻辑学是关于信息表达和推理中普遍存在的模式;其二为以内容为导向的,即逻辑学是某种认知科学,并伴有与其经验范围间的某些特定联系。也有的将逻辑学看作是一种研究“思想的规律”、语言和意义的“普遍语法规则”、全部可能本体论的柏拉图全域、人类认知的基础或者人类或机器所做的信息过程抽象的结构的科学等。

　　总之逻辑的推理形式除了演绎之外,还有非演绎的推理,这些推理也可以采用适当的方法进行形式化的处理。逻辑应该关注形式化的事情,比如语言和系统限制、多样性的结构等。逻辑学主要部分包括表达力、演绎力和计算力等问题。同时逻辑也应该是一般的法则,包括语言与本体论的平衡、组合性、复杂性的保持、翻译等内容,总之逻辑应该是一个多元的跨学科的专业。