3.4 我国货币政策对不同类型城市房地产价格的影响程度分析
3.4.1 城市类型的划分
3.4.1.1 城市类型划分标准
对我国区域的传统划分方式是以地理位置为依据,将我国划分为东部、中部以及西部地区,但是这种传统划分方式,并不适用于房地产市场,因为地理位置并非影响房地产市场的主要因素,同是一个地区的城市,房地产价格存在显着差异,因此,为了准确的分析货币政策对于不同类型城市影响的差异,本文要对我国房地产市场进行细分。参照我国社会科学院财政与贸易经济研究所提出的划分标准,以政治地位、经济实力、城市规模、区域辐射力为划分依据,将我国城市划分为一二三四线。具体划分结果如下:
一线城市:北京、上海、广州、深圳、天津二线城市,具体又细分为四类,即二线强:南京、武汉、沈阳、西安、成都、重庆、杭州、青岛、大连、宁波二线中:济南、哈尔滨、长春、厦门、郑州、长沙、福州、乌鲁木齐、昆明、兰州、苏州、无锡二线弱:南昌、贵阳、南宁、合肥、太原、石家庄、呼和浩特准二线:佛山、东莞、唐山、烟台、泉州、包头三线城市,具体又细分为三类,即三线强:银川、西宁、海口、洛阳、南通、常州、徐州、潍坊、淄博、绍兴、温州、台州、大庆、鞍山、中山、珠海、汕头、吉林、柳州。
三线中:拉萨、保定、邯郸、秦皇岛、沧州、鄂尔多斯、东营、威海、济宁、临沂、德州、滨州、泰安、湖州、嘉兴、金华、泰州、镇江、盐城、扬州、桂林、惠州、湛江、江门、茂名、株洲、岳阳、衡阳、宝鸡、宜昌、襄樊、开封、许昌、平顶山、赣州、九江、芜湖、绵阳、齐齐哈尔、牡丹江、抚顺。
三线弱:本溪、丹东、辽阳、锦州、营口、承德、廊坊、邢台、大同、榆林、延安、天水、克拉玛依、石河子、南阳、濮阳、安阳、焦作、新乡、日照、聊城、枣庄、蚌埠、淮南、马鞍山、连云港、淮安、丽水、衢州、荆州、安庆、景德镇、新余、湘潭、常德、郴州、漳州、清远、揭阳、梅州、肇庆、玉林、北海、德阳、宜宾、遵义、大理。
四线城市:上述城市以外的所有城市3.4.1.2 研究对象的选择
根据上述划分标准,考虑到房地产价格的地域差异性,以及数据的可得性,本文在一线、二线强、二线中、二线弱、三线城市中选择各省省会城市、直辖市、自治区首府城市、计划单列市共 35 个,作为研究对象进行实证研究,具体类别如下:
第一类:北京、上海、广州、深圳、天津第二类:沈阳、大连、南京、杭州、宁波、青岛、武汉、重庆、成都、西安第三类:长春、哈尔滨、福州、厦门、济南、郑州、长沙、昆明、兰州、乌鲁木齐第四类:贵阳、南宁、南昌、合肥、呼和浩特、太原、石家庄第五类:海口、西宁、银川.
3.4.2 数据的收集与处理
鉴于数据的可得性,本节选用我国 35 个大中城市的新建住宅价格指数、金融机构各项贷款余额、地方财政一般预算性收入以及全国的广义货币供应量、银行间30 天同业拆借加权平均利率、存款准备金率 2006 年-2012 年的年度数据作为样本。
为了分析我国货币政策对不同类型城市房地产价格的影响程度,需要将我国 35个大中城市的新建住宅价格指数、金融机构各项贷款余额、地方财政一般预算性收入,按照城市类别分别取平均值,来代表五类城市各指标的数值。
为提高数据的可比性,需要将价格因素的影响予以剔除。其中,对银行间 30天同业拆借加权平均利率 R 进行价格因素影响剔除时,采用的是银行间 30 天同业拆借加权平均利率 R 减去通货膨胀率的方法得到实际利率。对其他各指标则采用各指标除以居民消费价格指数的方法剔除价格因素的影响。
为了降低异方差的影响,对除银行间 30 天同业拆借加权平均利率的所有数据进行对数化处理,处理后的数据分别用 LPi、LM2、LLi、LRd、LYi表示,其中 i 表示城市类别。
3.4.3 实证分析结果与讨论
3.4.3.1 平稳性检验
为了避免出现伪回归,要对模型中各变量进行平稳性检验。对于非面板数据,使用 ADF 法检验其平稳性,对于面板数据,使用 levin,lin&chu 法检验其平稳性。
仔细观察表 3-4 不难发现,所有原序列拒绝原假设所犯错误的概率均大于 0.05,所有原序列经一阶差分后的序列拒绝原假设所犯错误的概率均小于 0.05,给定显着性水平 5%,则所有原序列均无法拒绝原假设,而一阶差分序列均拒绝原假设,也就是说所有原序列均是非平稳序列,而一阶差分序列均是平稳的,即所有原序列均是一阶单整序列。
3.4.3.2 协整检验
由于单位根检验中各变量同阶单整,因此各变量间可能存在长期的均衡关系。
为了确定各变量之间是否存在长期稳定的关系,则需要对进行协整检验。协整检验结果如表 4-2 所示:
面板数据协整检验的方法分为两大类,一类是建立在 EG 两步法的基础上的Pedroni 检验和 Kao 检验,另一类是建立在 Johansen 检验基础上的 Fisher 检验。由于本文所选取的样本时间跨度较短,不能运用 Fisher(combined Johansen)方法进行面板数据协整检验,因此,本文使用了 Pedroni 检验和 Kao 检验来对变量之间是否协整关系进行验证。Pedroni 检验共有 7 个检验统计量,如果大多数统计量均拒绝原假设,则我们可以认为变量之间是存在协整关系的,与此同时,在小样本下,Pedroni检验的 ADF 更为有效。从表中不难看出,在 Pedroni 检验的 7 个统计量中有 4 个统计量的 p 值均小于 0.01,也就是说给定显着性水平 0.01,大多数统计量均是统计意义上显着的,同时 Pedroni 检验的 ADF 统计量均是统计意义上显着的,也就是说,各变量之间是存在长期协整关系的。此外,Kao 检验的协整检验的 p 值为零,这也表明各变量之间存在长期的均衡关系,由此,可以建立面板数据模型。
第一,确定面板模型的估计形式。
在固定效应模型还是随机效应模型的选择中,使用 Hausman 检验,其 p 值为 0.0003,也就是说给定显着性水平 5%,拒绝“随机效应模型有效”的零假设,因此,固定效应模型更为有效,同时本节研究的是货币政策对房地产价格影响的城市差异性,选择固定效应模型也是适宜的。因而,可以建立面板固定效应模型:
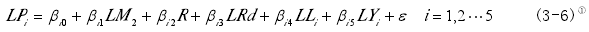
第二,面板模型的估计。
考虑到截面异方差问题,使用 Cross-section weights 法进行加权,并将数据代入式(3-6)中,则可得到的协整关系的估计结果见表 3-6:
从固定效应部分可以看出,在无其他因素影响的条件下,各类城市的房地产价格水平。其中,一线城市和二线强城市的房地产价格水平普遍较高,而后三类城市的房地产价格水平相对较低。这与城市发展水平的高低息息相关。一线、二线强城市的各方面发展水平都要远高于二线中、二线弱以及三线城市,其房地产价格水平必然会比后三类城市的房地产价格水平要高。
从长期均衡模型的拟合结果可以得出以下结论:
第一,长期模型的拟合优度为 95.85%,也就是说模型所选择的变量能较好的解释房地产价格的变动。F 统计量 p 值为 0.0007,DW=1.87,也就是说,给定显着性水平 0.05,模型中变量是联合显着的,且不存在一阶自相关。
第二,模型中某些变量是不显着的,说明该变量不是影响该类城市房地产价格的主要因素。对于一线和二线强城市来说,财政收入不是影响该类城市房地产价格的因素;货币供应量因素对二线中城市的房地产价格没有显着性影响;而存款准备金率不是二线弱城市房地产价格水平的影响因素。
第三,各类城市房地产价格影响因素及大小的分析。
其一,货币供应量与金融机构各项信贷余额是对各类城市房地产价格影响的主要因素,对房地产价格的变化起到了重要作用。一方面,一线、二线强、二线弱及三线城市的货币供应量弹性分别为 0.5060%、1.7052%、1.1306%、1.3052%,也就是说货币供应量每增加 1%,各类城市的房地产价格分别增加 0.5060%、1.7052%、1.1306%、1.3052%.货币供应量对二线强城市的房地产价格影响相对最大,而对一线城市的影响相对最小,也就是说,货币供应量对一线城市房地产价格的调控效果相对有限;另一方面,金融机构各项信贷余额每增加 1%,各类城市的房地产价格分别增加约 0.7802%、1.2194%、1.1068%、1.0098%、1.3097%,金融机构各项贷款余额对三线城市的房地产价格影响相对最大,而对一线城市的房地产价格影响相对最小,这表明金融机构各项信贷余额对一线城市的房地产价格的长期调控效果十分有限。
其二,利率水平与存款准备金率大小对各类城市的房地产价格均有影响,但不是很大,并且利率与存款准备金率对各类城市房地产价格的影响幅度大体相同。利率每增加 1 个单位,各类城市房地产价格会大体下降 0.0334%,特别地,利率对二线强城市的房地产价格影响幅度相对最小,利率每增加 1 个单位,二线强城市的房地产价格会下降 0.0140%.而存款准备金率每增加 1%,各类城市房地产价格会下降约 0.076%左右,存款准备金率对二线强城市的影响幅度相对最大,存款准备金率每增加 1%,二线强城市的房地产价格会下降 0.0951%.
其三,财政收入因素对综合发展水平较低城市的房地产价格影响更为明显。一方面,诸如与房地产市场相关的税种:土地增值税、城市土地使用税、房产税等的增加,会增加房地产的购买成本,从而减少居民对住房的需求,使房地产价格有一定程度的下降;而另一方面,个人所得税的增加,会使居民的可支配收入减少,从而降低居民购买住房的需求。因此,地方财政收入是各类城市的房地产价格有着显着性的影响,而各类城市的地方财政收入的不同,致使我国房地产价格存在城市差异性。长期均衡模型正好反映出了这一点。国家财政收入每增加 1%,二线中、二线弱及三线城市的房地产价格分别降低 0.0407%、0.0461%、0.0669%,作用效果依次增强。
其四,从各影响因素对各类城市房地产价格的影响大小来看,影响一线城市房价的主要因素为利率与存款准备金率;货币供应量与存款准备金率是影响二线强城市房价的主要因素;影响二线中城市房价的主要因素为利率、金融机构各项贷款余额及财政收入;影响二线弱城市房价的主要因素为财政收入与货币供应量;金融机构各项信贷余额及财政收入是影响三线城市房价的最主要因素。
3.4.3.3 向量误差修正模型
通过数据平稳性检验及协整检验,所有变量均是 I(1)变量,由此可以进一步建立向量误差修正模型,来分析变量间的长期均衡与短期波动的关系。
根据长期协整模型,可得其残差序列:
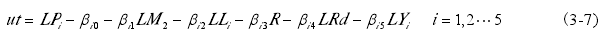
将式(3-7)滞后一期,代入并估计式(3-8),则可建立向量误差修正模型

从向量误差修正模型的拟合结果不难看出:
总体来看,首先,误差修正项的调整系数在统计意义上均是显着的,且均为负值,这表明滞后一期的非均衡误差对房地产价格具有反向调整作用,当产生负的非均衡误差时,房地产价格上升,反之则房地产价格下降。同时,误差修正项的系数大小大体相同,均在 2.05 左右,这表示各类城市的变量由短期关系转回长期均衡状态的速度是大体相同的。
其次,在影响方向上来看,货币供应量对房地产价格在短期内具有正向影响,而利率、存款准备金率、财政收入因素对房地产价格具有负向影响。
最后,在影响程度上来看,影响房地产价格最主要的短期因素为货币供应量,各类城市金融机构各项信贷余额因素不是房地产价格的短期影响因素。而造成各类城市金融机构各项贷款余额对房地产价格长期有影响而短期无影响的原因是我国货币政策传导渠道不畅通,以及金融机构各项信贷余额的变化对房地产市场产生影响具有时滞性而引起的。
具体来看,第一,货币供应量因素对五类城市都有显着性的影响,其中对一线城市的房地产价格影响最大,货币供应量每增加 1%,该类城市的房地产价格约上涨 1.5516%.在长期,货币供应量因素并不能影响二线中城市的房地产价格,而在短期,该因素对二线中城市的房地产价格有显着性影响,货币供应量每增加 1%,二线中城市的房地产价格约上涨 0.9164%.综合来看,在短期内货币供应量对一线城市房地产价格的影响要大于对二线城市房地产价格的影响,而对三线城市的房地产价格的影响相对最小,这主要是因为一线城市为我国最发达地区,各方面的发展都走在我国的前列,这使得房地产升值空间大,投资机会多,二线城市近年来虽快速崛起,吸引了众多投资商,但其房地产市场仍要取决于消费市场,而三线城市经济发展相对落后,投资较少,货币政策传导能力较差,房地产价格主要依赖于经济发展状况。
第二,在短期内,利率、存款准备金率以及财政收入因素对三线城市的房地产价格没有显着性的影响,也就是说这三个因素不是短期内影响三线城市房地产价格的主要因素,而对一线、二线城市的房地产价格的影响在统计意义上是显着的,但影响幅度不是很大。对一线城市来说,利率每降低 1 个单位,该类城市的房地产价格上升 0.0568%;存款准备金率每降低 1%,该类城市的房地产价格上升 0.0628%;财政收入每降低 1%,该类城市的房地产价格约上升 0.0068%.
纵向来看,利率、存款准备金率、财政收入因素对一线城市房地产价格的影响要大于对二线城市房地产价格的影响,也远高于三线城市,但总体来讲,各因素对各类城市房地产价格的影响幅度差异都不是很大。一方面,在短期内通过利率、存款准备金率来调控房地产价格是不太有效的。其原因主要表现在:我国三线城市房地产市场的发展较一、二线城市仍是不成熟的,各类金融机构、金融系统包括制度体系的发展都是不够完善的,再加上经济发展的相对落后,致使货币政策传导渠道不畅,货币政策效果不显着。另一方面,通过调整财政收入来改变房地产价格,在短期内效果也不显着。这是因为财政收入的主要来源是税收,财政收入的调整很大意义上是税收收入的变化,这就与我国的财政政策紧密相关。增加税收的财政政策对于一线城市来说,由于其本身的发展水平相对较高,其增加的税收收入的数额一定会大于二、三线城市的数额,同时一线城市无论从体系、制度、机构等各方面的完善性,以及政策执行力上来说,都要高于二、三线城市,因此财政收入对于房价的调整效果出现差异。此外,财政政策的实施也是具有一定时滞性的,因此,财政收入对房价的短期影响效果并不显着。
3.4.3.4 Granger 格兰杰因果检验
分别对各类城市通过基于 VAR 模型的 Granger 因果检验来判断我国货币政策与房地产价格之间的因果关系,并根据 AIC 和 SBC 准则确定模型的滞后阶数为 1,结果如下所示:
从上述结果不难看出,给定 5%的显着性水平,利率分别是一线城市、二线强城市、二线中城市及二线弱城市房地产价格的格兰杰原因,而其他因素均不是其房地产价格的格兰杰原因。也就是说,利率有助于解释一线城市、二线强城市、二线中城市及二线弱城市房地产价格的未来变化。而三线城市的金融机构各项贷款余额及地方财政一般预算性收入是其房地产价格的格兰杰原因,而其余因素均不是三线城市房地产价格的格兰杰原因。





