我们从中有针对性的选取了电气机械和器材制造业、食品制造业、水的生产和供应业、批发业和零售业等 18 个重点管理行业进行分析。
4.3.3 建立面板数据模型
面板数据模型根据截距项向量和系数向量中各分量的不同可以划分三种类型:无个体影响的不变系数模型(混合模型)、变截距模型、含有个体影响的变系数模型:形式一:无个体影响的不变系数模型的单方程回归形式可以写成【2】

判定规则:如果不拒绝假设2H 则可以认为样本数据符合不变系数模型,检验结束;如果拒绝假设2H ,则检验假设1H .如不拒绝假设1H ,则认为样本数据符合变截距模型;若拒绝1H ,则认为样本数据符合变系数模型。
根据以下公式计算:【3】
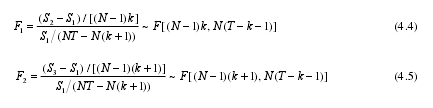
其中,1S2S3S 分别为变系数模型、变截距模型和混合模型的最小二乘残差平方和,k 表示解释变量个数,N 为观测单元个体数,既截面的个数(行业个数),T 为样本期数。
4.3.4 实证分析
在建立面板数据模型之前,我们首先进行单位根检验,来判断序列的平稳性。单位根检验结果如下:【4】
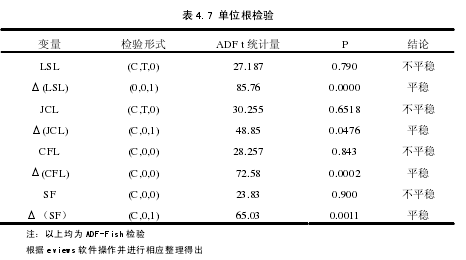
从上面的单位根检验可以发现这些变量都是一阶单整,对他们进行协整检验,结果如下:【5】
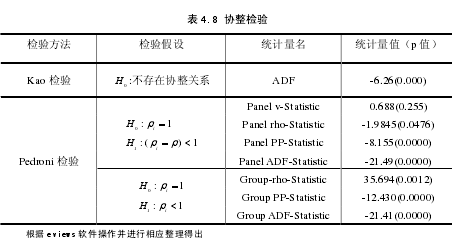
上述检验结果检验的样本区间为 2006-2011 年,从以上结果可以发现 Panelv-Statistic 的检验量的 p 值是 0.255,其他的都拒绝原假设,我们可以认为昆明市18 个重点行业的面板数据存在协整关系。
根据 2006-2011 年,昆明市 18 个行业的面板数据,使用 Eviews 6.0 计算得到1S =0.0267,2S =0.0688,3S =0.3026,T =6,k =3,N =18.由公式(4.4)和(4.5)可得检验统计量1F =1.05,2F =5.47. 利用函数得到 F 分布的临界值,其中 d 是临界点, 和 是自由度。在给定 5%的显着性水平下(d=0.95),得到相应的临界值为: (68,36) =1.67; (51,36) = 1.68.
由于 1.68,所以拒绝 ;又由于 1.67,所以不拒绝 .因此,通过计算我们发现拒绝变系数模型和不变系数模型,因此采用变截距模型。根据对个体影响的形式不同,变截距模型又分为固定影响模型变截距模型和随机影响变截距模型两种。通过 Hausman 检验可以看出,模型的 W 统计量大于临界值,这说明模型拒绝个体影响与解释变量不相关的原假设,再结合具体情况,本文选取了昆明市 18 个重点行业的截面数据,故应当将模型中的个体影响确定为固定影响模式。
使用 Eviews6.0 软件,计算结果如下:【6】
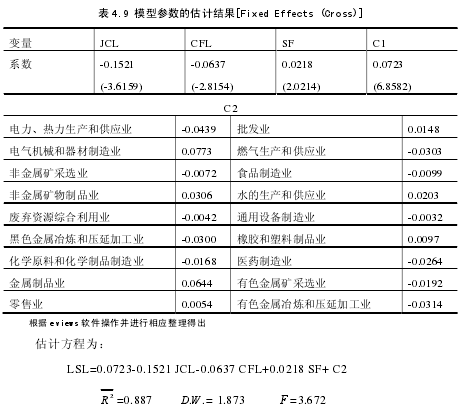
由2R 和 F 的值可知,模型拟合优度很高且总体线性关系显着。 DW 接近 2说明模型不存在自相关。JCL,CFL,SF 的系数均能通过 t 检验,这说明检查率,处罚力,税负对流失率的影响显着。
由上式可以看出,检查率,处罚率与流失率成反向关系,而税负与流失率成正向关系。而检查率对流失率的影响程度最大,税负对流失率的影响程度最小,因此,在实际操作中,可以通过提高检查力度来达到降低增值税流失率。





