
近年来随着高层建筑功能的多样化,各种竖向不规则的复杂高层建筑结构大量涌现,其中主要包括带转换层的结构、带加强层的结构、错层结构、连体结构和多塔结构等.
这些结构竖向布置不规则,传力路径复杂,有些工程平面布置也不规则.
我们将建立具有代表性的平面不规则底层框支剪力墙结构为分析对象,对于转换层设置在1层、2层的框支剪力墙结构,可近似采用转换层与其上层结构的等效剪切刚度比γe1表示转换层上、下层结构的结构刚度变化,γe1宜接近1,非抗震设计时γe1不应小于0.4,抗震设计时γe1不应小于.我们所建的模型属于平面不规则结构,根据规范规定应计算双向水平地震作用下结构的扭转效应.
通过改变上部剪力墙的厚度来改变转换层上、下侧向刚度比,并对结构进行相应的计算分析,从中总结出转换层上、下刚度比对结构扭转效应的影响.
1、周期比和位移比对扭转的影响
周期比是指结构扭转为主的第一周期Tt与平动为主的第一周期T1比.结构扭转第一自振周期与地震作用方向的平动第一自振周期之比值,对结构的扭转效应有明显影响,当二者接近时,结构的扭转效应显著增大.徐培福推导出了考虑平动—扭转耦联反应的计算公式,并给出了考虑平动—扭转耦联的计算公式.他根据考虑平动扭转耦联的计算公式绘制了θr/u与Tt/T1的关系图(θr/u为结构相对扭转响应,该比值反应扭转振动效应的程度).从中可以看出耦联反应对结构的扭转效应有明显的放大作用,设计中应考虑平动—扭转耦联反应.同时可以看出当周期比>0.8以后,结构相对扭转响应增大很快.
为了控制耦联反应对结构的扭转效应的放大作用,文献中做了如下规定:在考虑偶然偏心影响的规定水平地震作用下,复杂高层建筑(包含带转换层结构)扭转为主的第一周期Tt与平动为主的第一周期T1之比不应大于0.85.位移比是指在考虑偶然偏心影响的水平地震作用下,楼层竖向构件的最大水平位移(层间位移)与该楼层平均位移(平均层间位移)的比值.研究表明,扭转效应越大,位移比越大.假定楼板为平面内无限刚,当一个结构发生平动和扭转时,将发生如图1所示的变形.
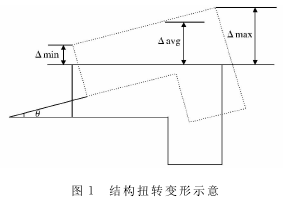
从图1可以看出,当位移比逐渐增大时,整个结构的变形受力将变得非常不均匀.结构在地震作用下将在变形最大的竖向构件处首先破坏,从而造成结构破坏.为了控制楼层变形的均匀性,文献中做了如下规定:在考虑偶然偏心影响的规定水平地震作用下,复杂高层建筑结构(包含带转换层结构)不宜大于该楼层平均值的1.2倍,不应大于该楼层平均值的1.4倍.从另一个角度来分析,控制结构扭转变形的实质是控制结构扭转变形小于结构平动变形或者控制结构扭转变形的绝对值比较小,控制地震作用下结构扭转振动效应不成为主振动效应,避免结构扭转破坏.
2、算例及基本参数
模型共26层,平面布置分别见图2、图3.各跨长度均为8m,平面凹进l=16m,l/Bmax=0.5,所以平面凹进尺寸大于相应方向总尺寸的30%,模型为凹凸不规则结构.
转换层位于第二层,底部两层为框支结构,由落地剪力墙和框架组成,层高4.5m;转换层上部为剪力墙结构,共24层,层高为3m,结构总高为81m.
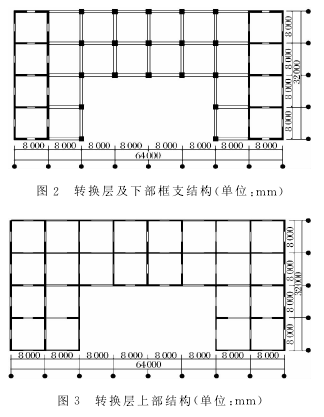
算例1结构各跨长度均为8000mm,底层框架梁截面尺寸为400mm×800mm;二层转换梁分为两种:上部两侧均布置剪力墙的转换梁截面尺寸为700mm×1000mm,上部一侧布置剪力墙的转换梁截面尺寸为700mm×1200mm;底部两层的柱截面尺寸均为1200mm×1200mm;底部剪力墙厚度为400mm,转换层上部剪力墙的厚度为350mm;转换层楼板的厚度为250mm,其余各层楼板厚均为150mm.
转换梁、柱及底部两层剪力墙的混凝土强度等级为C50,底层框架梁及上部剪力墙的混凝土强度等级为C40,楼板的混凝土强度等级为C35.算例2~4分别为将上部剪力墙的厚度变为300mm、250mm、200mm,其余部位不变,结构的整体模型见图4.
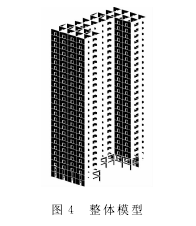
3结构的动力分析
运用大型分析软件SAP2000对结构进行分析,本框支剪力墙结构按8度(0.2g)设防,场地类别为Ⅱ类场地,设计地震分组为第二组,特征周期Tg=0.4s,恒荷载组合值系数为1,活荷载组合值系数为0.5.
3.1动力特性分析
采用Rits向量法对结构进行模态分析,计算取24阶振型,得到结构对应的自振周期、模态振型参与质量比、固有振型等动力特性,由4种结构模型的分析结果得振型参与系数的累计值均为0.99,满足规范当中90%的参与系数的要求,说明所取的振型数能够满足计算精度的要求,模型1~4的自振周期及模态振型参与质量比见表1(取前3阶振型).
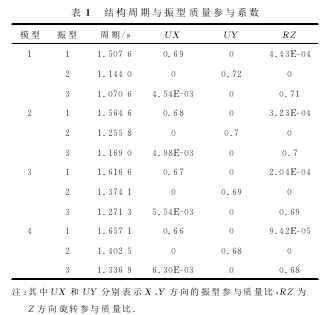
通过表1可以判断:
(1)结构的第一振型是X方向的平动,第二振型为Y方向的平动,第三振型为绕Z轴的扭转振型,振型存在平动—扭转耦联现象;(2)当上层剪力墙厚度分别为350mm、300mm、250mm、200mm时结构的周期比分别为0.7101、0.7471、0.7864、0.8068.
3.2反应谱分析及弹性时程分析
高层建筑结构宜采用振型分解反应谱法进行分析,而对于带转换层的结构应采用弹性时程分析法进行多遇地震下的补充计算.
地震波的合理选择是时程分析的基础,选择EL-Centro(N-S)地震波(记录时间为30s,加速度峰值为341.7cm/s2,记录时间间隔0.02s)、Taft地震波(记录时间为54.38s,加速度峰值为175.945cm/s2,记录时间间隔0.02s)、兰州波共三条地震波记录作为激励,地震持续时间定为20s.
当取三组时程曲线进行分析时,结构地震作用效应宜取时程分析法计算结果的包络值与振型分解反应谱法计算结果的较大值.(1)扭转效应分析经分析得出结构竖向构件X向位移值,见表2.
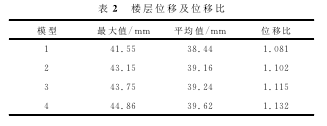
均匀改变转换层上部剪力墙厚度对结构竖向构件最大水平位移及平均位移影响不大,上部剪力墙厚从200mm增至350mm时结构的位移比有一定降低.
3.3层间位移分析
经分析对比所得层间位移如图5所示.
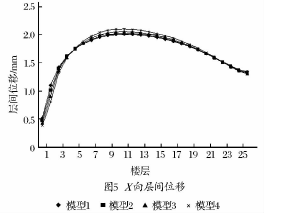
由图5可得各模型的层间位移角均能满足文献的要求.4种模型的楼层层间位移最大值都出现在11层,对于上部墙体较厚的结构由于转换层上、下的侧向刚度变化较大、地震作用大等原因,下部框支层层间位移大于较薄剪力墙的结构的层间位移.由于侧向刚度较小,模型4的中间楼层最大层间位移明显大于其他模型.
4、结论
(1)均匀增大墙厚改变转换层上、下侧向刚度比对结构的低阶振型周期有一定影响,可以降低结构的位移比及扭转效应.
(2)对平面不规则长形和平面尺寸较大的结构,应在考虑位移比的同时充分考虑扭转对结构周边构件的影响,防止构件扭转破坏.
(3)对平面不规则带梁式转换层结构应在考虑控制转换层上、下侧向刚度比的同时,适当增大结构周边抗侧刚度,合理调整刚心附近抗侧构件的刚度.





