
空间结构的技术水平是一个国家土木建筑业水平的重要衡量标准,也是一个国家综合国力的体现,因此世界各国对空间结构技术的发展一直给予高度的重视。改革开放30多年来,随着国民经济的高速发展和综合国力的提高,我国空间结构的技术水平也得到了长足的进步,正赶超国际先进水平。大跨度空间结构的社会需求和工程应用逐年增加,空间结构在各种大型体育场馆、剧院、会议展览中心、机场候机楼、各类工业厂房等建筑中得到了广泛应用。特别是近几年,随着北京2008奥运会、上海2010年世界博览会等国家重大社会经济活动的展开,我国在近10年内建成的一大批高标准、高规格的体育场馆、会议展览馆、机场航站楼等社会公共建筑,这给我国空间结构的进一步发展带来了良好的契机,同时也对我国空间结构技术水平提出了更高的要求。
平板网架结构在工程实际中已经得到了广泛的应用,经过多年的经验积累和摸索,其设计理论和计算方法基本上已经十分成熟。但是随着人们对建筑物净空距离要求的不断提高,网架结构的跨度也在不断的增大,致使整个工程项目造价增加。一个好的工程结构不但要做到美观实用,而且还要做到精简、节约。这样便要求在工程项目的设计过程中,适时地引入优化设计,以达到降低工程造价的目的。目前,网架结构的优化设计存在的主要问题有:①在现有的网架结构优化设计研究中,往往是针对确定性情况下的优化设计,通常将工程实际中大量存在的不确定性因素和模糊因素忽略不计。②多数的网架结构的优化设计模型,并没有考虑结构可靠性。
本文的主要目的是应用模糊数学方法,尝试建立网架结构的模糊优化设计模型;并在此基础之上引入可靠度约束条件,建立基于可靠性的网架结构模糊优化模型。主要包括以下3方面:结构内力的计算;模糊优化模型的建立;编制程序及算例分析。
1 结构内力的计算
假定网架结构的计算模型为空间铰接杆系结构,即节点铰接,杆件仅承受轴向力,忽略节点刚度的影响,不计次应力对杆件内力所引起的变化。模型试验和工程实践都说明这个假定是完全许可的,所带来的误差可忽略不计。结构材料为线弹性、各向同性。网架结构的外载荷按静力等效原则集中作用在网架节点上。荷载作用下,杆件变形很小,符合小变形原理。
任何结构的设计计算包括优化设计都是以工程结构的简化计算模型为基础,在明确了实际结构将要承受的荷载,通过不同的方法计算得到结构中各个构件的内力之后展开的。平板网架结构也不例外,常用的计算方法有交叉梁系差分法、拟夹层法、空间析架位移法(空间杆系有限元法)等。其中,空间杆系有限元法是目前网架结构计算精度最高的一种方法,适用于各种类型、各种支撑的网架计算,本文中算例的内力采用有限元软件ansys加以计算。
2 模糊优化模型的建立
(1)建模中单元类型及实常数的确定。网架结构的有限元模型杆件单元和弦节点质量单元的类型分别采用link8单元及Mass21质量单元。link8是三维杆单元,模拟工程中三维空间桁架、绳索、铰链以及弹簧单元,可以承受单向拉伸或压缩。该单元具有2个端部节点,每个节 点上 有3个自由度。Mass21质量单元为一个有6个自由度的质量单元,作为节点力加载。网架结构有限元模型杆件单元的实常数即指单元的横截面面积。
(2)模糊优化变量的选择。与常规优化模型不同的是,在模糊优化模型中设计变量、目标函数、约束条件,三者可以都是模糊的,也可以只有某一个方面是模糊的而其他方面是确定的。只要包含了一个方面的模糊性,该优化模型就是模糊优化问题。本文所建立的网架结构模糊优化模型中,只有设计变量、约束条件是模糊的,目标函数是确定的。
3 网架的内力和变形分析
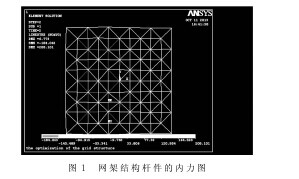
该钢网架结构ansys分析得到的内力如图1所示,从中可以看到,由于是对称加载,应力图对称分布。上弦杆受压,下弦杆受拉,斜杆拉压。最大应力杆件 编 号 为96,杆 件 受 压 为 斜 腹 杆 对 应 应 力 为-208.09MPa.最小应力杆件编号为33,杆件受拉为下弦杆对应应力为176.72MPa.利用ansys分析得到的该钢网架结构的变形图如图2所示,从中可以看到各个截面位置处的挠度,整体延x轴上下对称,支点处挠度都为0.最大位移位于 编 号 为7的 节 点 (图2中MX处),数 值 为6.773mm.从力学上分析,该节点位于4个支撑点之间,同时该节点输入的节点荷载也比较大,所以位移最大是有可能的。【图1.2】

4 模糊优化算例对比分析
通过定义杆件壁厚T1~T6为设计变量DV,节点变形DZMAX和杆件应力SMAXE为状态变量SV,整个网架结构的总体积VTOT作为目标函数OBJ的优化程序以达到优化的效果。其中假设Fj、Xj和Fj-1、Xj-1分别为目标函数、设计变量第j次迭代和第j-1次迭代的结果(Xj为矢量),Fb和Xb分别是当前的最优目标函数和其相应的设计变量值。
如果满足|Fj-Fj-1|≤τ或者|Fj-Fb|≤τ,τ为目标函数的公差(取0.01),那么认为迭代收敛,于是迭代停止。假设|Xj-Xj-1|≤τ或者|Xj-Xb|≤τ,那么也认为设计变量的搜索已经趋于收敛,于是迭代停止。优化求解定义为一阶优化,迭代次数为20次。
表1所列是优化迭代次数1~21部分数据,由于迭代过程中10次以后数据的变化在很小的范围内,所以省略9~19次的优化结果。原始数据为迭代循环次数为1的结果,所以共有21次迭代。将最优化的结果与原有设计数据进行对比,如表2所列。整体用钢量的变化趋势,如图3所示。从表1数据可以看出,在满足强度和刚度以及在确定范围的情况下,优化设计的目标函数值比原设计值减小了将近8.26%,从图3也可以直观看出用钢量经过优化的变化趋势,可见模糊优化设计的经济效益是比较可观的。【表1图3】
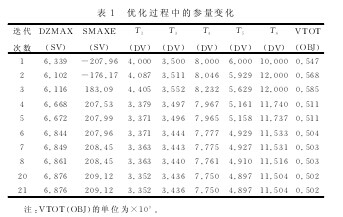
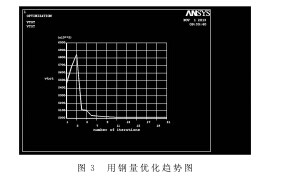
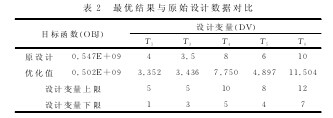
表2所列第6种杆件的壁厚比原设计值有所增加,这是在约束模糊化的情况下,为保证应力和刚度的要求而重新协调的结果。【表2】
5 结束语
采用通用工程分析软件验证专业软件设计的网架结构,增加了设计结果的可信度。先进行整体分析,找出关键的节点对其进行局部分析,有利于结构的优化和创新。在不知道具体设计变量的最优解时,可以预先定义一个值,再通过优化设计定义设计变量的取值范围,满足设计要求的情况下以得到最优解,对实际的工程具有一定的指导意义。本文正是运用这种方法对网架结构的计算和分析,在满足强度和刚度以及在确定范围的情况下,考虑模糊因素的网架结构模糊优化设计是可行的,并且经济效益可观。
〔参考文献〕
[1] 董石麟,赵阳.论空间结构的形式和分类[J].土木工程学报,2004,37(1):7-12.
[2] 董石麟,马克俭,严慧,等.组合网架结构与空腹网架结构[M].杭州:浙江大学出版社,1992.
[3] 张炳华,侯昶.土建结构优化设计(第2版)[M].上海:同济大学出版社,1998.
[4] 王云仓.基于ansys的结构优化设计方法[J].水科学与工程技术,2005(S1):11-12.
[5] 韩维涛,张亚新.ansys优化技术在零件结构设计中的应用[J].机械研究与应用,2005(6):92-94.
[6] 刘建明.基于可靠性的网架结构模糊优化设计[D].大连:大连理工大学,2005.
[7] 完海鹰,黄炳生.大跨空间结构[M].北京:中国建筑工业出版社,1994.
[8] 王新敏.ansys工程 结 构数 值 分析 [M].北京:人民交通出版社,2007.
[9] 刘涛.精通ansys[M].北京:清华大学出版社,2002.
[10]邢静忠.ansys7.0分析实例与工程应用[M].北京:机械工业出版社,2004.
[11]杨松林.工程模糊论方法及其应用[M].北京:国防工业出版社,1996.





