
随着汽车工业的迅猛发展,中国废旧轮胎的产量大幅上升。废旧轮胎因具有很强的抗热、抗生物、抗机械性,很难降解,因而被人们称为黑色垃圾,且易引发诸多环境问题。利用废旧轮胎制作橡胶,并加入混凝土中生产橡胶混凝土,成为近年来备受关注的一种新型材料。虽然胶粉的加入使得混凝土的各项力学性能降低,但不可否认的是橡胶混凝土却在抵抗变形,防止开裂,提高韧性方面有积极作用。由于橡胶混凝土材料是多相、非均质的复合材料,其构件的开裂,发展及最终破坏所表现出来的表面裂缝分布的不确定性,模糊性等特点,同时还要考虑到结构所处实际环境条件等一系列因素,使得构件表面各种性质裂缝交错混杂,难以有效描述。
近20年来,由Mandelbrot创立的分形理论不断发展,应用到多个学科,这主要是由于它可以将难以定量描述的复杂对象用一种较为便捷的定量方法表述出来。笔者就通过对橡胶混凝土梁进行抗弯性能试验,用分形维数定量描述荷载与梁裂缝之间的关系,为橡胶混凝土梁的开裂和破坏过程的非线性研究提供一种新思路。
1、实验描述
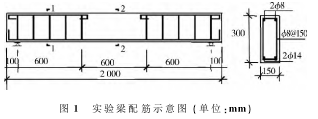
在试验的过程中,做一根普通混凝土梁和一根橡胶混凝土梁。试件的尺寸为长×宽×高=150mm×300mm×2 000mm,分别编号为L-0、L-15。混凝土的配合比为水泥∶砂∶石子∶水=1∶1.21∶2.46∶0.42,选用热轧钢筋HRB335(屈服强度为390Mpa),配筋率为0.766,设计等级为C30,梁的配筋情况如图1所示。其中,橡胶混凝土梁用胶粉代替原来15%体积的沙子,试件制备好后在标准养护室养护28d,依据《GB 50152-92混凝土结构试验方法标准》对试件进行三点受弯试验,利用智能裂缝测宽仪测定不同荷载下裂缝的宽度,并用黑水笔勾勒出裂缝开展趋势,直至梁破坏.
2、实验装置
利用油压千斤顶采用单调静载法,通过压力传感器控制荷载等级。试验主要测试橡胶混凝土梁的受弯性能,所以加载方式是三分点法。千斤顶的荷载通过分配梁作用,对称的加载在试验梁上,形成试验梁跨中600mm的纯弯段,排除剪应力对橡胶混凝土梁的受弯性能影响。实验现场布置图如图2。

3、混凝土梁裂缝分形维数的计算
裂缝生长细节虽然是不规则且随机的,但它是否具有分形特性尚需进行验证,只有裂缝发展满足自相似性才认为具有分形特征。计算分形维数的方法主要有:标尺法、盒计数法及分岛法。其中,盒计数法较为方便可行。其具体做法是:以边长为r的正方形网格去覆盖整个裂缝分布区域,计录含有裂缝的网格数目N(r),通过不断改变格子尺寸r来改变网格密度并计录覆盖有裂缝的格子数。如果对不同的r,式(1)成立则认为裂缝分布具有统计意义上的子相似性,式(2)中D就是裂缝分布的分维数。
根据黑水笔勾勒出的裂缝开展趋势线以及破坏后的裂缝分布照片,利用CAD将其绘出,如图3。
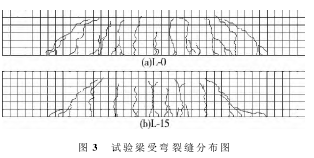
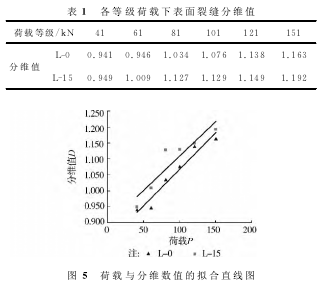
对梁表面裂缝分布采用盒计数法进行分维统计,并进行线性拟合,图4为绘得的两根梁在破坏状态下的lnN(r)-lnr图,并将两根梁在不同荷载下计算出的分维数值列于表1
通过对试件裂缝进行lnN(r)-lnr线性拟合,lnN(r)-lnr成良好的线性关系,从而可以得出裂缝分布具有统计意义上的自相似性,证明了采用分形理论来描述裂缝发展情况的可行性。
4、实验结果分析
4.1裂缝分形维数与荷载之间的关系研究
表1为两根梁荷载等级与分维值之间的关系,从表1中可以看到,随着荷载的增大,分形维数也逐渐增大,将荷载与分维数值进行拟合,得到图5
从图5中通过混凝土梁与橡胶梁的对比,橡胶混凝土梁裂缝的分维数值大于普通梁的裂缝分维值。造成这一现象的原因可能是胶粉的加入,一方面提高了混凝土变形能力,降低了混凝土内部应力集中现象;另一方面胶粉同混凝土材料分别属于有机与无机,两者交界面是薄弱面,受力后易产生细小裂纹。另外,各根梁的分形维数数值与荷载等级之间呈线性递增关系。由于实验数据有限,难以定量描述胶粉掺入量与分维值之间的关系。
4.2裂缝分形维数与裂缝宽度之间的关系研究
表2是根据实验记录的两根梁裂缝宽度的数据结合试验梁各个荷载等级下分维值D(由于151kN时弹性梁已破坏,故不参与讨论)列出的数据,并绘制出并绘制出D-ωmax关系曲线,如图6
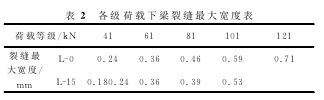
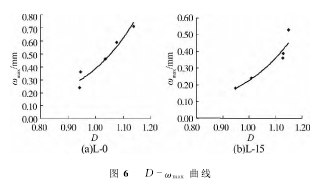
从表1和表2中看出,随着荷载的增大,分形维数逐步增大,裂缝宽度也逐渐增大,在小荷载下橡胶混凝土的裂缝宽度在同等级荷载作用下明显小于普通混凝土梁,但当达到破坏荷载后,橡胶梁的最大裂缝宽度又大于普通混凝土梁。可能的原因是初始时,试件在小荷载作用下,裂缝发展较慢,胶粉的掺入使得混凝土的抗裂性能变强,但却降低了混凝土的抗压强度,因而首先达到破坏荷载,在151kN力的作用下破坏,裂缝宽于普通梁。

L-0和L-15最大宽度和表面裂缝分维值之间的关系分别由公式(3)、(4)给出

式中:
D为各等级荷载作用下试验梁表面裂缝分维值;?恚幔?橇逊炜矶茸畲笾怠Mü?耸剑?梢缘玫搅逊熳畲罂矶扔敕治??抵?浯笾鲁手甘?菰龉叵档某醪浇崧郏?谑潜憧筛?荼砻媪逊旆治?道赐频汲隽旱鼻昂稍叵铝逊炜矶鹊拇笾路段АJ芟抻谑匝槭?荩?荒芄坏贸鱿鸾夯炷?亮逊煊敕治?档亩ㄐ怨叵担??玫较鸾翰袅慷曰炷?亮逊炜矶燃胺治?档牧炕?叵祷剐韪?嗍笛楹透?钊氲难芯俊?
5 结论
实验应用分形理论研究橡胶混凝土梁的裂缝发展程度,通过研究得到以下主要结论:
1)通过对两根混凝土梁最终破坏时裂缝的发展结果分析,进一步研究了混凝土梁表面裂缝分布的统计自相似分形性质,验证了采用分形理论研究橡胶混凝土梁裂缝的发展情况的可行性。
2)利用盒计数法计算具有自相似性的两根混凝土梁表面裂缝的分形维数,研究了裂缝分形维数与裂缝宽度之间的对应关系,并得到试验加载的荷载等级越高,混凝土表面裂缝分形维数增大的结论。
3)研究表明,橡胶混凝土梁表面裂缝分形维数随裂缝宽度的增大而增大,因此,橡胶混凝土梁表面裂缝的分形维数可以作为评价橡胶混凝土梁破坏程度及安全程度的一个指标。
4)橡胶混凝土梁的裂缝分形维数大于普通混凝土梁,裂缝宽度小于普通混凝土梁,有效提高了混凝土梁的抗裂性。
参考文献:
[1]张昊,张小亮,乐金朝.废旧轮胎橡胶改性混凝土材料性能试验研究[J].浙江水利水电专科学校学报,2008,(1):39-41.
[2]孙家瑛,高先芳,朱武达.橡胶混凝土研制及物理力学性能研究[J].混凝土,2001,(5):30-32.
[3]孙洪泉.分形几何与分形插值[M].北京:北京科学出版社,2011.
[4]Sun H Q,Ding J,Guo J,et al.Fractal research on cracks ofreinforced concrete beams with different aggregates sizes[J].Advanced Building Materials(Advanced Materials Research).2011:1818-1822.
[5]李维涛,孙洪泉,邢君.分形几何理论在混凝土研究中的应用[J].河北工业大学学报,2003,32(6):13-16;
[6]Mandelbrot B B.Fractal geometry of nature[M].SanFrancisco:W.H.Freeman and Co.,1982.
[7]李维涛,孙洪泉,邢君.混凝土中的分形效应初探[J].水利与建筑工程学报,2004,2(3):17-19.
[8]崔亚平,陈宝义.分形理论在混凝土损伤表面的应用[J].山西建筑,2005,(12):53-54.
[9]国强,邓学钧.水泥混凝土微裂纹演化的混沌分析[J].重庆交通学院学报,1996,(3):22-26.
[10]曹茂森,任青文,翟爱良,等.混凝土结构损伤的分形特征实验分析[J].岩土力学,2005,26(10):1570-1574





