
4.2.1 平稳性检验
由于时间序列数据大多是非平稳的,因此在进行协整分析前必须检验数据平稳性,否则可能会出现伪回归现象,使协整关系失去意义。若一个非平稳的时间序列经过 d 次差分之后平稳,则该序列为 d 阶单整,记做 I(d)。本文选取得检验方


首先根据样本数据的趋势图大致判断 Ln JOB、Ln Z 和 Ln GDP 的平稳性。从趋势图 4-1 至 4-3 可以看出,三者均呈现了随时间增长而上扬的趋势,并非围绕均值上下波动,因此均为非平稳时间序列。为了进一步确定差分阶数,我们根据 ADF检验值与临界值作一个比较。


由表 5-1,各个时间序列的 ADF 检验结果显示,在显着性水平为 1%的条件下,各变量均接受原假设,即存在单位根,说明该序列为非平稳时间序列;在一阶差分条件下,ADF 值小于 1%时的临界值,即拒绝原假设,不存在单位根,时间序列平稳。
4.2.2 协整检验
协整检验是对非平稳的时间序列进行分析,探究各变量之间的长期均衡关系。其思想是:如果各变量的时间序列是非平稳的,但他们的线性组合具有平稳性,则他们存在协整关系。目前协整检验有 EG 两步法和基于 VAR 的 johansen 检验等方式,EG 两步法主要针对两个变量,而多个单整变量的协整检验一般采用 johansen协整检验。Johansen 检验并非一次独立检验,而是针对变量的连续检验,共检验N 次,最多存在 N-1 个协整关系,其优势在于可以发现全部的协整关系,并且检验功效更稳定。本文将采用 johansen 检验方法,然后运用 ADF 检验残差的平稳性。
ADF 检验结果表明,所有时间序列均为一阶单整,因此可以进行协整分析。下文运用 johansen 检验法对就业总量、GDP、财政总支出进行协整分析。由于协整方程对滞后期的选择十分敏感,因此首先根据 AIC 和 SC 准则确定最优滞后阶数;在得到协整方程后,为避免虚假协整,还需对残差进行单位根检验。
首先,对 Ln JOB 和 Ln GDP、Ln Z 进行 VAR 模型的滞后期检验,确定最优滞后期。检验结果如表 4-3.从表中可以看出,SC 准则选择 P=2,LR 检验统计量和其余 4项准则均选择 P=3,综合考虑 VAR 模型的最优滞后阶数为 P=3.然后对各个变量进行协整关系分析,结果如表 4-4 所示: 协整检验表明在 5%的显着水平下,就业量和 GDP、财政支出总量之间存在长期均衡关系,协整方程如下:
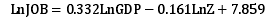
为确保协整关系有意义,针对上述协整结果对残差进行平稳性检验,从趋势图中可以看出残差值围绕零值上下波动,具有平稳性;ADF 的检验结果也表明在1%的显着水平上,残差的 ADF 值为-5.12<-3.67 残差序列平稳。这表明根据johansen 检验方法得到的就业量和 GDP、财政支出总额之间的协整关系具有统计学意义。同样,对世界银行和统计年鉴的就业量进行检验,得到结果如表 4-5.

从表 4-5 可以看出,上述三种就业量数据得到的协整关系都反映了相似的结果,即我国 GDP 长期以来和就业呈正相关关系,系数为 0.33 至 0.59 之间,而财政支出总量对就业为负相关,系数为-0.16 至-0.20.
4.2.3 格兰杰因果关系检验
协整检验表明我国就业量和 GDP、财政支出总量存在长期均衡关系,但不能得出就业量和 GDP、财政支出总量的因果关系,因此下面用格兰杰因果关系检验方法,验证因变量和自变量的因果关系。检验结果如表 4-6 所示:
检验结果表明,在 10%的显着性水平下,GDP 和财政支出总量的改变是引起就业量变化的格兰杰原因,而就业量改变不是导致财政支出变化的格兰杰原因,即GDP 和就业之间是双向因果关系,财政支出总量与就业是单向因果关系。
4.2.4 VAR 模型和脉冲响应分析
在变量存在长期均衡关系的基础上,进一步对变量做脉冲响应分析,以探究财政支出总额对就业量的动态影响。为确保脉冲响应分析结果的准确性,首先建立VAR 模型并进行单位根检验。
1.VAR 模型
通过对就业量、GDP、财政支出总额三者建立 VAR 模型,将参数估计的结果写成如下矩阵形式:

得到 VAR 模型后,对模型进行单位根检验,检验结果如表 4-7.由于模型的滞后长度为 3 并且有 3 个内生变量,所以模型存在 9 个单位根,其中 1 个实根 8 个复根。这些根的模都小于 1,即所有的根都在单位圆内,说明估计的 VAR 模型是稳定的,可以进行脉冲响应分析。
2.脉冲分析
通过脉冲响应分析,可以得出财政支出总量变化时,对就业量的动态影响,即一单位的财政支出总额的冲击对就业量的影响。
从图 4-5 可以看出,GDP 始终对就业产生正向影响,影响效果呈波动趋势,并在第 5 年时达到最大,此后呈先减弱后增强趋势;财政支出总额对就业具有抑制作用,其负向冲击在第 3 年时达到最大,此后冲击效果逐渐减弱并趋于 0.
4.2.5 结果说明
通过对 1981-2013 年数据的实证分析,对就业量、财政支出总量和 GDP 的检验结果得出如下结论:
(1)就业量、财政支出总量、GDP 三者长期均呈现上升趋势,原序列都为非平稳时间序列,但一阶差分后的序列平稳,并且能够通过 ADF 检验和协整检验,说明三者长期中存在均衡关系。
(2)从协整方程可以看出,我国的经济增长和就业二者之间存在正向的关系,GDP 每增加 1%就会带动就业量约 0.332%至 0.586%的增加;财政支出总额对就业量有负向影响,财政支出每增加 1%就会引起就业量约 0.161%至 0.197%的减少。从脉冲图来看,财政支出总额短期和长期对就业都具有抑制效果,并在第 3 年达到顶峰,随后负向冲击效果减弱并逐渐趋于 0.
4.3 财政支出结构的就业效应

4.3.1 平稳性检验
为避免虚假回归,在协整分析前要检验数据的平稳性,当所有变量处于同阶单整时方可进行协整关系检验。下面仍采用 ADF 单位根检验方法,对上述 6 个变量进行单位根检验,检验结果如下表所示:


由表 4-7 看出,各个时间序列的 ADF 检验结果显示,在显着性水平为 10%的条件下,各变量均接受原假设,即存在单位根,说明序列为非平稳时间序列;在一阶差分条件下,ADF 值小于 10%时的临界值,即拒绝原假设,不存在单位根,时间序列平稳。
4.3.2 协整检验
ADF 检验结果表明,所有时间序列均为二阶单整,因此可以进行协整分析,下文运用 johansen 检验法对就业总量和财政投资性支出等进行协整分析。由于协整检验对于滞后期十分敏感,不当的滞后期选择会使结果有很大差异,本文根据 AIC和 SC 准则确定最优滞后阶数为;为避免虚假协整,在得出协整方程之后对残差进行单位根检验。
首先,对 LnE 和 LnTZ、LnJY、LnKJ、LnSB 进行 VAR 模型的滞后期检验,确定最优滞后期,检验结果如表 4-9.从表中可以看出,LR 检验统计量和其余 4 项准则选择 P=1,综合考虑 VAR 模型的最优滞后阶数为 P=1.然后对各个变量进行协整关系分析,结果如表 4-10 所示:
协整检验表明在 5%的显着水平下,就业量和财政投资性支出等 4 个变量之间存在长期均衡关系,并给出了包含以上 5 个变量的协整方程:

为确保协整关系显着,避免虚假协整,对上述等式的残差进行平稳性检验,检验结果表明,在 1%的显着性水平上残差的 ADF 值为-5.28,小于-3.67,说明残差序列平稳,就业量和各项财政支出之间的协整关系具有统计学意义。同样,对世界银行和统计年鉴的就业量进行检验,得到结果如表 4-11.
从表 4-11 可以看出,上述三种就业量数据得到的协整关系都反映了相似的结果,即我国财政教育支出对就业的促进作用相对明显,系数达到了 0.46 至 1.12;社会保障支出对就业虽然有正向作用,但系数仅有 0.004 至 0.078 之间;同样,财政投资支出对就业影响较小,系数基本在零值附近;财政科技支出对就业有负向影响,除统计年鉴的数据系数较小,可能与 1990 年前后就业量统计标准有关,其他两个数据的系数分别达到了-0.405 和-0.759,负向影响较为显着。
4.3.3 格兰杰因果关系检验
协整检验表明我国就业量和以上五类财政支出存在长期均衡关系,但不能得出就业量和财政支出的因果关系,即财政支出增加导致就业量改变,还是就业量改变导致财政支出增加,因此下面用格兰杰因果关系检验方法,验证因变量和自变量的因果关系。检验结果如表 4-12 所示:
检验结果表明,在 5%的显着性水平下,财政教育支出、的改变是引起就业量变化的格兰杰原因,而就业量改变不是导致以上两项支出变化的格兰杰原因,即上述两项财政支出与就业之间是单向因果关系;而财政科技支出和投资支出的改变是引起就业量变化的格兰杰原因,同时就业量改变也是引起他们变化的格兰杰原因,这两项支出与就业之间是双向因果关系。这就意味着,可以根据财政支出和就业量之间的格兰杰因果关系,合理的调整财政支出结构,从而达到增加就业的目的。
4.3.4 VAR 模型和脉冲响应分析
在变量存在长期均衡关系的基础上,进一步对变量做脉冲响应分析,以探究财政支出各个变量对就业量的动态影响。为确保脉冲响应分析结果的准确性,首先建立 VAR 模型并进行单位根检验。
1.VAR 模型
通过对就业量与财政投资支出、教育支出、科技支出、社会保障支出、行政管理支出建立 VAR 模型,将参数估计的结果写成如下矩阵形式:
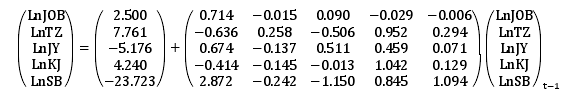
得到 VAR 模型后,对模型进行单位根检验,检验结果如表 4-13.由于模型的滞后长度为 1 并且有 5 个内生变量,所以模型存在 5 个单位根,其中 3 个实根 2个复根。这些根的模都小于 1,即所有的根都在单位圆内,说明估计的 VAR 模型是稳定的,可以进行脉冲响应分析。
2.脉冲分析
通过脉冲响应分析,可以得出财政支出的各个变量变化时,对就业量的动态影响,即一单位的财政支出的冲击对就业量的影响。
从图 4-6 可以看出,在短期中财政投资支出和社会保障支出对就业为负向冲击,两者均在第 6 年前后冲击达到峰值,此后逐渐减弱;财政教育支出和行政管理支出对就业一直保持正向冲击;财政科技支出开始为负向冲击,在第 6 年时冲击为 0,此后转为正向冲击。
4.3.5 结果说明
通过对 1981-2013 年数据的实证分析,对就业量和财政投资支出、教育支出、科技支出、社会保障支出、行政管理支出的检验结果得出如下结论:
(1)就业量和上述 5 项财政支出长期均呈现上升趋势,原序列都为非平稳时间序列,但二阶差分后的序列平稳,并且能够通过 ADF 检验和协整检验,说明就业量和财政支出长期中存在均衡关系。
(2)从协整方程可以看出,长期中财政教育支出对就业量有正向的影响,并且效果较为明显;财政科技支出对就业量具有明显的抑制作用,而社会保障支出和投资支出对就业量产生的影响微弱,系数不到 0.1.从脉冲图来看,在短期中财政投资支出和社会保障支出对就业为负向冲击,财政教育支出和行政管理支出对就业一直保持正向冲击,财政科技支出开始为负向冲击,在第 6 年时冲击为 0,此后转为正向冲击。
4.4 实证分析结论
通过对我国 1981-2013 年的数据分析,可以得到如下结论:
(1)就业量和 GDP、财政支出总量三者存在长期均衡关系,其中 GDP 对就业的带动效果明显,GDP 每增加 1%会使就业量增加 0.332%至 0.586%;财政支出总量长期中对就业有抑制作用,财政支出总量增加 1%会使就业减少 0.161%至 0.197%.
(2)从财政支出结构来看,就业量和财政投资支出、科技支出、教育支出、社会保障支出具有长期均衡关系,其中教育支出对就业的促进作用相对明显,系数达到了 0.46 以上,社会保障支出对就业虽然有正向作用,但系数仅有 0.004 至0.078 之间;同样,财政投资支出对就业影响较小,系数基本在零值附近;财政科技支出对就业有负向影响,并且较为显着。





