摘 要: 组合图形面积教学是小学数学教学内容中比较重要的一部分,也是教学中的重点和难点内容。组合图形是由几个简单的图形组合而成。组合图形的面积教学本身涉及的知识点较多,学生在解决求几何图形的面积时,往往觉得看花容易绣花难,讲得头头是道,下笔错误连篇。究其原因,是缺乏有序的思考过程和正确的解题格式。本文就如何有序引领学生思考与规范答题,谈谈自己的实践与思考。
关键词: 小学数学; 组合图形面积; 教学实践;
一、小学数学组合图形面积教学现状
1. 基础不牢,公式错用
小学数学图形面积公式虽然不多,但一旦综合运用却很容易出错。如教学五年级上册组合图形的面积时,学生运用三角形、梯形面积公式时老是忘记除以2,导致公式错用。究其原因,不是不理解公式中为什么会除以2,更不是不会背公式,而是受平行四边形面积公式的影响,受图中数据的干扰——图中数据没有2。所以学生一见到题目中的数据,也就没有深入动脑去想是什么图形用什么公式了,直接就把图中数据拿来组合算式,全然不顾公式推导过程中强调的除以2了。过后让这类学生分析错题错因,他们往往一看就知道自己错了,倍感遗憾地说都是“粗心”惹的祸。作为教师,决不能将学生的错误简单地归结为粗心,深挖粗心背后深层次的原因,仍是答题习惯不好所致。
2. 教学枯燥,缺乏创新
组合图形本身涉及的知识点和内容较多,学生们掌握起来有一定难度。如果单凭老师讲学生听,学生被老师牵着鼻子走,一直处于一种被动状态,必然导致很多学生听课效率低,这样是起不到很好的效果的。教学时,如何启发学生有序思考,调动学生主动去动脑,这是教学的关键。
以往老师对于这一个难点教学,较多采用讲授法,往往容易落入牵着学生走的俗套。如在教学五年级上册求下面组合图形的面积时,老师通常会带领学生一起思考这个图形不是我们学习的规则图形,怎样使它变成规则图形呢?学生自然会想到分割法、添补法,进而再按老师的引导分别求出转化后的规则图形,即分别求出长方形和梯形的面积,最后再求总面积。这样的教学方式,表面上看似顺利到位,实际上学生的思考更多地被老师代替,故一下笔错误百出。
二、小学数学组合图形面积教学的具体措施
1. 教学采用“总——分——总”思路
这一难点问题,总结学生的错因如下:有的只算了其中的一个部分,尤其是图形复杂,分割出两个以上的图形时,部分学生往往会漏算其中的一个平面图形,或者所有的图形都分别算完了,但最后求组合图形总面积时又漏加其中的某一个图形,还有的同学错用公式导致算错。仅仅是粗心吗?粗心背后的根源是:1.部分学生思路散乱,思考无序。2.解题习惯不好,公式能记住但又用错,解题只看题目中的数据,没有深入去思考题目以外的公式中的数据。如三角形、梯形面积老是忘记除以2。

为了避免同样的错误再次发生,这里的关键在于:如何启发学生去解决这一问题?在解决这一问题的过程中,学生应该经历怎样的思考过程?这才是我们要重点关注的;而所谓解决问题,则是“醉翁之意不在酒”——解决问题只是一个“驱动性任务”,任务驱动背后的数学思考,才是这一学习任务的关键。在教学中,我尝试了用“总——分——总”的思路引导学生学会思考,收到了不错的效果。首先是“总”,即设计总体思路。面对一个组合图形,采用什么办法把它转化成学过的规则图形,并在图上分一分、画一画、添一添,然后列出解决问题的总体规划。这样的问题能真正启发学生主动思考,激起学生思维的火花,学生的思维过程很快便会显现出来。在相互碰撞中,有的采用割补法,有的采用添补法,生生互动,师生互动,创如朝阳。接下来便是“分”,即在总体思路的指引下,应该分别计算哪些规则图形的面积。最后又回到“总”,将分别计算到的图形面积再次回应总体思路,按总体规划的思路解决求组合图形的面积。通过这样的思路引领,学生的思维激活了,思考更有序了。
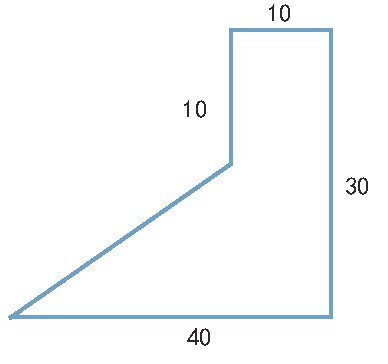
2. 答题采用“总——分——总”格式
良好的书写格式是提升学生解题正确率的重要条件。为提升学生的解题正确率,我要求学生严格用“总——分——总”的格式解答组合图形的面积。如上图的“总”可以是分割法:S总面积=S长方形+S梯形;也可以是添补法:S总面积=S长方形_S梯形。“分”,即分别计算,上题如果用分割法,则要分别计算出分割出来的一个长方形与一个梯形的面积.计算过程中,为了学生准确利用公式,我特别强调利用公式代入求值的方法进行计算,即公式写在前,计算跟在后,这样,忘记除以2的学生大大减少。第三步再次回到“总”,即又回到第一步总体规划,将分别计算到的图形面积再次回应总体思路,要么是用加法求总面积,如果是添补法,则是用减法求总面积。
三、取得的效果
通过“总——分——总”的教学模式,“总——分——总”的答题步骤,学生解决组合图形的兴趣大大增强,正确率也大大提升,学生的解答书写如下图:

当学生们沉浸在一道道需深度思考,才能解决的组合图形面积的题目中时,他们尝到了思考的乐趣;当他们欣赏着一道道自己用“总——分——总”三步法解决好的组合图形面积题目时,他们尝到了成功的喜悦。
观察上述学习过程,当求组合图形面积的“被动学习”因“总——分——总”三步法而主动化后,学生必然会自觉地根据问题的需要,主动地对已有素材进行观察、分析、比较,进而或抽象、或符号化、或模型化。这一过程,发展的恰恰是学生的各项核心素养。利用“总——分——总”解决组合图形的面积问题,过程貌似艰辛,但它却锤炼了学生的数学思考,发展了学生的数学创造,有效提升了学生的数学核心素养。





