计量经济学模型论文（优选范文6篇）

　　计量经济学模型可以简洁有效地描述、概括某个真实经济系统的数量特征，更深刻地揭示出该经济系统的数量变化规律，所以本篇文章就为大家介绍几篇计量经济学模型论文范文，供给大家参考一下计量经济学模型论文的写作手法。

计量经济学模型论文优选范文6篇之第一篇：计量模型下我国钢材产量的影响因素分析

　　摘要：钢材是工业生产重要的原材料成分， 任何重工业中都需要用到钢材。通过我国2006年-2017年钢铁产量以及其影响因素的时间序列数据， 利用计量经济学模型分析我国钢铁产量以及其影响因素的关系。结果表明， 粗钢产量与焦炭产量对钢材产量有明显的影响关系， 并针对结论从政府、钢材生产企业以及钢材贸易企业三方面提出了未来钢材市场的建议。

　　关键词：钢材产量； 计量经济学模型； 最小二乘法； 逐步回归法；

　　1 引言

　　钢材是工业生产中重要的原材料成分， 主要分为螺纹钢、卷板、线材三大类， 在工业中房地产投资， 桥梁建造， 汽车、船舶等交通工具建造都需要用到钢材。随着我国钢材行业规模的不断扩大， 每年钢材产量不断提高， 在国民经济众多方面都起到了很好的作用。

　　但是我国钢材行业也存在着很大的问题， 钢材排放气体不达标严重污染环境， 钢材生产量没有管制等， 所以， 通过研究钢材产量的影响因素， 可以很好地解决我国钢材存在的问题。

　　2 理论分析

　　根据钱纳里工业化阶段理论， 人均国内生产总值 （GDP） 在800~4800美元时处于工业化阶段中期， 城市化率在30%-60%之间；人均GDP在4800~9000美元处于工业化阶段后期， 城市化率在80%以上。我国目前正处于工业化后期阶段， 峰值可能在2020年前后。我国2017年人均GDP8836美元， 但我国经济发展不平衡现象非常严重， 尽管东部地区工业化和城市化已达到较高水平， 但中西部地区发展还具较大潜力， 我国钢材消费潜力还很大。并且我国钢材行业面临着各种问题， 国家优惠政策消除开始限产、没有核心领导企业等， 通过钱纳里工业理论可以找到我们现存的阶段， 从而可以更好的分析钢材产量问题。

　　3 模型的设定

　　利用经济学知识分析可知， 钢材生产总量要受到粗钢产量、固定资产投资、国内生产总值和建筑业总产值等的影响， 因此可以将钢材生产产量 （Y） 看作被解释变量， 粗钢产量 （X1） 、全社会固定资产投资 （X2） 、国内生产总值 （X3） 、建筑业总产值 （X4） 、焦炭产量 （X5） 看作解释变量， 建立线性回归模型：

　　Y=C+β1*X1+β2*X2+β3*X3+β4*X4+β5*X5+μ

　　4 样本的收集

　　4.1 被解释变量

　　25-我国钢材产量， 代表每个月生产的钢材量。

　　4.2 解释变量

　　X1--粗钢产量 （粗钢， 即制造钢材的原材料， 由生铁经过火炉氧化脱去碳和其他杂质后得到的钢水， 之后在钢水中加入合金和碳， 浇铸成粗钢， 粗钢经过加过生成钢材， 粗钢是钢材生成的必经过程之一） .

　　X2--全社会固定资产投资 （全社会固定资产投资是以货币形式表现的建造和购置固定资产活动的工作量， 这些活动均需要钢铁来支撑， 对钢铁具有需求） .

　　X3--国内生产总值 （即GDP, 用来衡量一个国家或地区的经济状况的指标， 钢材是工业中的主要材料， 对一个国家或地区的经济状况有较大影响） .

　　X4--建筑业总产值 （建筑业总产值是以货币形式表现的建筑业企业在一定时期内生产的建筑业产品的总和。钢铁的主要用途为建筑， 建筑业的发展也会带动钢铁的生产量） .

　　X5--焦炭产量 （焦炭是钢材生产中重要的原材料之一， 钢材生产需要加入焦炭） .

　　表1 我国钢材产量及其影响因素

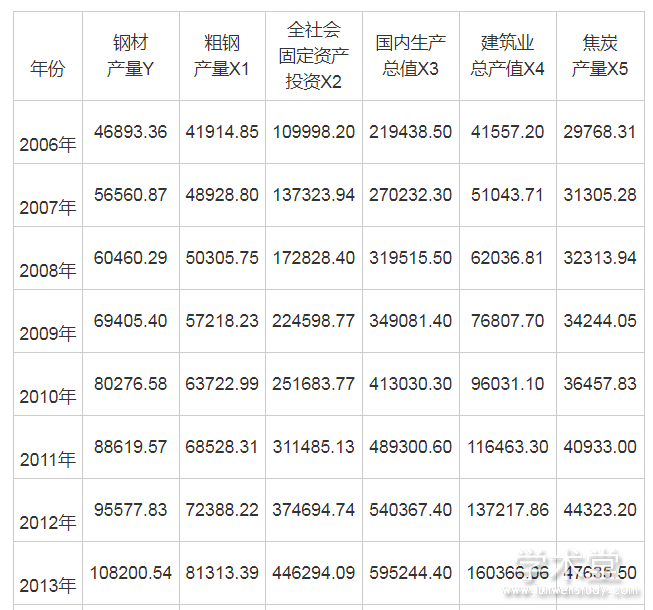
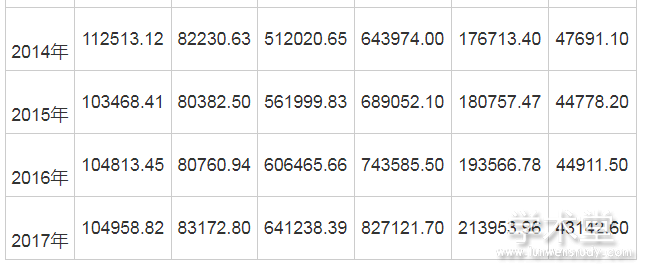
　　通过国家统计局网站搜集了2006年-2017年的钢材产量 （万吨） 、粗钢产量 （万吨） 、全社会固定投资 （亿元） 、国内生产总值 （亿元） 、建筑业总产值 （亿元） 、焦炭产量 （万吨） , 数据如上。

　　5 模型参数的估计

　　将上述数据导入Eviews利用OLS法得出以下结果：

　　变量C, X1, X2, X3, X4, X5的相关系数分别为-28565.43, 1.325011, -0.012777, -0.017904, 0.060938, 0.781406, Prob结果分别为0.0302, 0.0016, 0.6799, 0.6404, 0.7569, 0.0926, t-Statistic 结果分别为-2.823338, 5.462109, -0.433388, -0.491681, 0.324058, 1.998525, R-squared =0.997953, F-statistic=584.9149, Prob （F-statistic） = 0.000000

　　可以得出：

　　Y=-28565.43+1.325011*X1-0.012777*X2-0.017904*X3+0.060938*X4-0.781406*X5.

　　6 模型的检验

　　6.1 经济意义检验

　　X1的相关系数为正， 表明粗钢产量与钢材产量呈正相关， 从经济意义上来讲较合理。

　　X2的相关系数为负数， 表明全社会固定资产投资与钢材产量为负相关， 但从经济意义上来讲， 全社会固定资产投资越大， 钢材产量越多， 故从经济意义上来说不合理。

　　X3的相关系数为负数， 表明国内生产总值与钢材产量为负相关， 但从经济意义上来讲， 国内生产总值越大， 钢材产量越多， 所以从经济意义上来说不合理。

　　X4的相关系数为正， 表明建筑业生产总值与钢材产量为正相关， 从经济意义上来讲合理。

　　X5的相关系数为正， 表明焦炭产量和钢材产量呈正相关， 从经济意义上来讲合理。

　　6.2 统计检验

　　R2=0.997953, 表示拟合度高度相关

　　F值=584.9149, F检验高度相关

　　T检验中X1的T检验显著， 其他变量t检验显著性水平均大于0.05, 故t检验不通过， 可能存在多重共线性。

　　6.3 多重共线性检验

　　6.3.1 相关系数矩阵

　　根据理论分析可得共有5个解释变量， 包含过多的解释变量且T检验不通过， 可能存在多重共线性， 利用 Eviews 的相关系数矩阵得出各解释变量之间的关系， 相关系数矩阵表如表2.

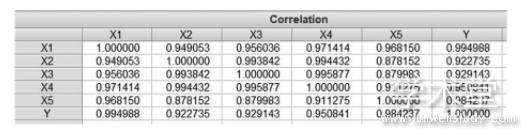
　　表2 相关系数矩阵表

　　由此表可看出钢铁产量与其他5个解释变量相关系数较大， 均为高度相关， 其他因素之间也是高度相关， 故存在多重共线性。

　　6.3.2 多重共线性的修正

　　采用逐步回归法， 根据参数估计结果得出， 拟合效果最好的为X1变量， 故以Y=C+β1*X1作为基本模型， 将其他解释变量逐一代入基本模型， 可以得出， 两个因素时X1, X5的R2最大， 且t检验最为显著， 之后在X1, X5两个因素中， 分别引入X2, X3, X4得出均无现实意义， 故拟合度最高且t检验显著水平高的模型为F （X1, X5） , 得出如下结果：

　　Y=-29021.62+1.024706*X1+1.149951*X5

　　将X1, X5相关数据代入Eviews中利用OLS法我们可以得出：

　　C, X1, X5的相关系数为-29021.62, 1.024706, 1.149951, t-Statistic的Prob分别为0.0000, 0.0000, 0.0013, F-statistic=1493.170, Prob （F-statistic） = 0.000000, R-squared=0.996995.可看出， 修正后的F检验较大， 且t检验概率均小于0.05, 都通过， R2拟合度也较好， 并且DW值=2.065284.接近于2, 表明变量接近正态分布， 这个方程可以很好地反应钢材产量主要受粗钢产量和焦煤产量因素的影响， 都是正向相关， 其他因素影响效果较差。

　　6.4 异方差性检验

　　通过多重共线性结果利用Glejser方法异方差检验， 得到以下结果：

　　F-statistic的值=0.170681, Obs*R-squared的值=0.438518, F检验以及Obs的伴随概率大于0.05显著性检验， 未通过异方差检验， 故不存在异方差性。

　　6.5 序列相关性检验

　　由于样本容量n=12, 无法进行D-W检验， 故用图示法来进行， 通过参数估计结果按照时间顺序绘制出残差如图1.

　　图1 残差图  

　　由以上图可以看出该数据可能存在负序列相关， 故运用Eviews进行迭代法， 假设存在一阶序列相关， 输出结果如下：

　　AR （1） 的Coefficient=-0.087732, t-Statistic=-0.251642, t检验不显著， 故不存在序列相关性。最终模型为

　　Y= -29021.62+1.024706*X1+1.149951*X5

　　7 结论

　　粗钢的产量以及焦炭的产量对钢材的产量影响是最明显的， 显然， 粗钢以及焦炭作为钢材生产过程中的原材料， 对于其产量影响是最为显著的， 其中， 最显著的是粗钢的产量其次是焦炭的产量， 而其他解释变量并没有想象中的那么显著， 可以看出， 我国钢材产量主要受供给因素 （粗钢产量、焦炭产量） 的影响， 而需求因素 （固定资产投资、国内生产总值等） 对其影响程度并没有供给因素那么明显， 可以看出我国钢材目前产能过剩问题严重。

计量经济学模型论文优选范文6篇之第二篇：基于计量经济学分析我国粮食产量的影响因素

　　摘要：粮食问题关系民生， 是各国普遍关注的问题。中国人口基数大、增长速度快， 保障粮食安全对促进社会和谐具有重要意义。根据官方数据， 通过模型设定、估计、检验、调整， 得出影响我国粮食产量的计量经济学模型。分析了影响我国粮食产量的主要因素， 提出了相关建议。

　　关键词：粮食产量； 影响因素； 计量经济学模型；

　　1 模型设定

　　基于对粮食产量影响因素的初步认知， 采用粮食作物播种面积 （千公顷） X1、水土流失治理面积 （千公顷） X2、农业机械总动力 （万千瓦） X3、自然灾害经济损失 （亿元） X4、耕地灌溉面积 （千公顷） X5、化肥施用量 （万吨） X6为解释变量， 用于解释粮食产量 （千公顷） Y.建立多元线性回归模型如下：

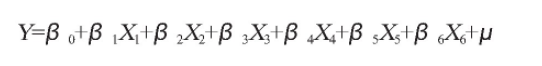
　　在初步建立模型基础上， 依次进行最小二乘估计、经济意义检验、统计学及计量经济学检验， 作相应调整， 得出我国粮食产量影响因素的计量模型。

　　2 数据收集

　　模型数据摘自中国国家统计局2017年公布的《中国统计年鉴》， 信息真实可靠， 以此为基础建立模型较有信服力[1].

　　3 模型估计、检验及调整

　　3.1 最小二乘估计

　　操作Eviews6.0软件对模型进行最小二乘估计 （OLS） , 回归结果如下：

　　3.2 检验与调整

　　3.2.1 经济意义检验

　　回归结果显示， 该模型中除X3农业机械总动力、X5化肥施用量除外， 其余解释变量的系数符号与实际经济理论符合， 初步通过经济意义检验。

　　3.2.2 统计检验

　　最小二乘估计结果显示， 可决系数调整后的R2=0.979 235, 表明粮食产量变化的97.92%可以由选取的6个因素共同变化来解释， 模型拟合程度较好。5%的显著性水平下， F=236.784 5>2.51, 通过F检验， 方程整体显著程度好。

　　但是从斜率项t检验值来看， X3、X5、X6的t检验值小于临界值， 3个因素对被解释变量影响不显著。

　　操作Eviews6.0软件制作各解释变量间的相关系数表， 初步判断出X1和X5、X3和X6之间存在较大相关性， 判断模型存在多重共线性。通过逐步回归进一步检验与修正， 逐步回归中， 剔除了解释变量X5、X6, 解决了多重共线性问题， 修正后回归结果为：

　　3.2.3 计量经济学检验

　　满足统计检验后， 采用怀特检验方法， 对模型进行异方差检验， 判断解释变量与随机干扰项之间是否存在关系影响同方差基本假定。根据怀特检验显示， 1%显著性水平下， P值大于α值， 模型通过P检验， 接受原假设， 即同方差假设， 修正后模型为：

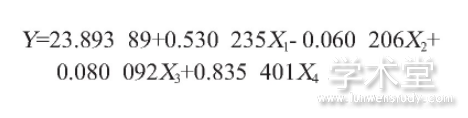
　　其中：Y为粮食产量；X1为粮食作物播种面积；X2为水土流失治理面积；X3为农业机械总动力；X4为自然灾害经济损失。

　　4 相关建议

　　一是加强防灾减灾意识， 通过成灾机理研究， 认识灾害发生发展规律， 进行监测预警。

　　二是恢复生态， 保护植被， 减少水土流失面积， 因地制宜配置资源。

　　三是优化农业基础设施， 完善水利灌溉， 推广节水灌溉技术， 提高防洪能力。

　　四是促进农业生产机械化， 提高农业生产效率。

　　参考文献
　　[1] 焦宇航。影响我国粮食产量因素的计量分析[J].魅力中国， 2014 （4） :303.