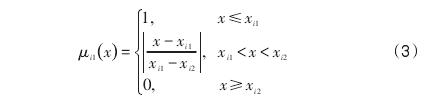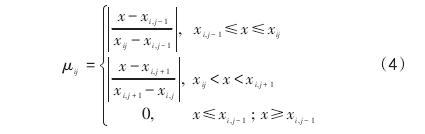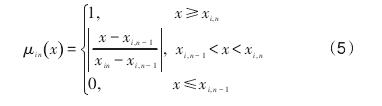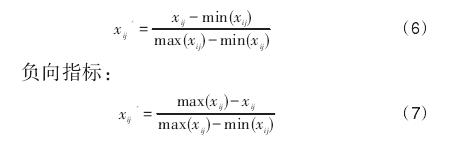0 引言
0 引言
2013 年 11 月在中国共产党十八届三中全会的纲领性文件 《中共中央关于全面深化改革若干重大问题的决定》 中提出了“探索编制自然资源资产负债表,对领导干部实行自然资源资产离任审计,建立生态环境损害责任终身追究制”的重大决策[1],探索编制自然资源资产负债表是新时期加强生态文明体制机制、健全资源节约利用、建设美丽中国的根本战略需求所在[2]. 水资源资产负债表是自然资源资产负债表在水资源主体上的具体应用,是今后落实最严格水资源管理制度、对领导干部实行自然资源资产离任审计和终身追究生态环境损害责任等的重要依据[3]. 水资源价格是编制水资产负债表的前提条件,如何对水资源赋予经济价值是其核心与难点所在。 目前采用直接出售价格法、水权交易法、供水成本法、完全成本法、影子价格法、CGE 模型法等方法,但不同估价方法对同一资产估算结果存在不尽相同、可靠性以及可比性不强等缺陷,水资源价格核算仍然是一个充满探索、实验的研究领域[4-5].
水资源是生态环境可持续发展的决定性因素,在水上如何合理、高效地利用有限的水资源是张掖市发展需要解决的根本问题,其中合理制定水价是基本手段之一[6-7]. 本文综合考虑水资源、水环境、经济社会等影响因素,将熵权法和层次分析法相结合,采用模糊数学综合评价模型,确定张掖市2010-2014年5 a水资源价值及价格动态变化趋势,为水资产负债表的编制提供方法数据参考和支撑。
1 水资源资产价格核算指标体系
1. 1 研究区域
甘肃省张掖市位于祁连山北麓黑河流域中游地段,属于典型的干旱绿洲农业区,张掖市集中了全黑河流域95%的耕地、90%以上的人口和89%的国内生产总值,是黑河流域中游社会经济发展和水资源利用最具影响的区域[8],该区域具有干旱区内陆河流域的典型特征,平均多年人均水资源量为 1 350 m3,地均水量为 7 950 m3·km-2,分别占全国平均值的 60%和 30%,水资源短缺,是中国首批建设节水型社会试点城市之一[9].
1. 2 数据获取
根据 2010-2014 年的 《张掖市统计年鉴》 和2010-2014 《张掖市水资源公报》,依据采用《国家地面水环境质量标准》(GB3838-2002)的污染程度分类制定水质等级标准以及 2010 年张掖市环境质量报告书,借鉴文献有关研究成果[10-12],指标选取代表性好、针对性强,易于量化,选择水量、水质、人口、社会经济、生态环境5个方面的准则层和 18 个指标作为张掖市水资源价格评价指标体系(表 1)。 各指标的分级情况可根据各评价因素的实际数值,对照各因素的分级指标推求,分为高、较高、中等、较低、低5类。
2 水资源价格模糊综合评价
模糊综合评价的基本思想是应用模糊关系合成的原理,根据被评价对象本身存在的形态或类属上的亦此亦彼性,从数量上对其所属给以刻画和描述[13]. 鉴于水资源系统的复杂性和模糊性,用模糊数学的概念和方法对水资源资产价值进行动态定量评价,由水资源价值评价模型和水资源价格计算模型两部分组成。
2. 1 水资源价值模糊综合评价模型
(1) 建立评价对象的指标集 V = f {X1,X2,X3,…,Xn},水资源价值要素集 V = {水量,水质,人口,社会经济,生态环境};
(2) 建立评价集 U = {μ1,μ2,μ3,…,μn},水资源价值的评价向量 W={高,较高,中等,较低,低};
(3) 单因素评价矩阵单因素评价矩阵Ri是分别以水量、水质、人口、社会经济、生态环境各评价指标的评价向量。 Ri定义如下:
Ri=ωо μ (1)
式中: ω为单因素中各评价因子的权重;μ 为通过各自的隶属度函数确定的各评价因子的隶属度矩阵。
(4) 模糊综合评价
V=Aо R (2)
式中: A =(a1, a2,…, an)为各因素对水资源价值的指标权重,且满足
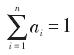
。R 为以水量、水质、人口、社会经济、生态环境各评价指标评价向量 Ri为基础构造的综合矩阵 .
2. 2 相对隶属度的确定
选用降半梯形分布,建立一元线性隶属函数:
当j=1时,
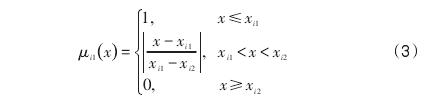
当j=2、3、4时,
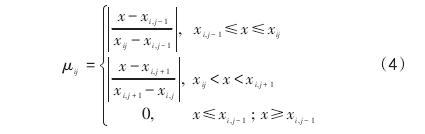
当j=5时,
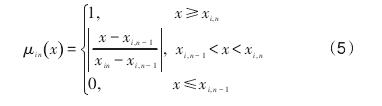
式中: x 为评价因子的实际值; xi,j- 1、xij为评价因子相邻两等级的设定标准值; i 为评价因子标号;j=2,3…n,n=5; μn(x)为评价因子 i 的隶属度。
2. 3 确定权重
2. 3. 1 层次分析法步骤
(1)对 每 一 层 次 各 因 素 的 相 对 重 要 性 1,2,…,9 及它们的倒数作为指标间相对重要性标度,构建指标两两对比判断矩阵;(2) 计算判断矩阵的特征根和特征向量,得到指标层对于要素层的重要性权值进行层次单排序;(3) 对判断矩阵进行一致性检验;(4) 进行层次总排序,得出各个评价指标对目标层的重要性权值。
2. 3. 2 熵值法应用步骤[14-15]
(1) 对 R 矩阵中的 Xij进行级差标准化处理得到新的矩阵R':
正向指标:
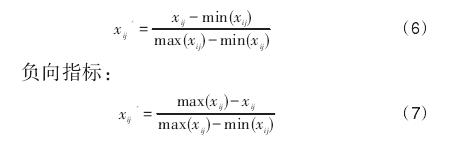
式中: xij为指标初始值;xij‘为标准化处理后的值;max(xij)、min(xij)为相应指标初始最大值、最小值。

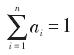 。R 为以水量、水质、人口、社会经济、生态环境各评价指标评价向量 Ri为基础构造的综合矩阵 .
。R 为以水量、水质、人口、社会经济、生态环境各评价指标评价向量 Ri为基础构造的综合矩阵 .