本篇论文目录导航:
【题目】人口红利对城乡收入的作用探析
【第一章】人口红利下城乡收入问题探究绪论
【第二章】城乡收入差距的测定方法及人口红利影响
【第三章】人口红利期我国城乡收入差距现状分析
【第四章】人口红利对我国城乡收入差距的实证分析
【结论/参考文献】基于人口红利的城乡收入差距研究结论与参考文献
4 人口红利对我国城乡收入差距的实证分析
由第三部分中对人口红利期的判定中,我们得知 1993 年至今为我国人口红利期。本部分将通过选取 1993-2012 年的时间序列数据,运用计量软件、建立合适的经济计量模型来实证人口红利对我国城乡收入差距的影响。在本部分里,将着重介绍以下三个方面:①通过第二部分中的理论分析途径来构建实证模型。②选择实证模型中需要的相关数据及相关指标,并对其数据选择进行说明解释。③通过对模型的实证分析过程进行说明和解释人口红利对我国城乡收入差距的影响程度。
4.1 实证模型构建
根据第二部分的理论分析来进行实证模型的构建。在人口红利期,存在最显着的两个特征是:高劳动参与率和低抚养比。在理论分析中,高劳动参与率会影响到城乡收入差距的变化。在人口红利期,由于特殊的人口年龄结构,存在大量的适龄劳动力,基于城乡工资的预期差异,会引起农村剩余劳动力的转移。在转移的过程中,产业结构的重心会向第二和第三产业的转移,产业结构的优化升级会促进城乡收入差距扩大。由于产业结构的优化升级会使城乡收入差距扩大,故选择第二三产业总比重作为第一个变量;在关于低抚养比的理论分析中,人口红利期需要负担的抚养人数比较少,基于人力资本投资预期,总抚养比下降会引起家庭人力资本投资的增加,但是由于城乡人力资本投资差异,会导致城乡收入差距扩大。根据上述分析,选择城乡人力资本投资差异为第二个变量进行研究。所以基于上述分析,通过选择第二三产业总比重和城乡人力资本投资差异来构建VAR 模型,来做出人口红利对我国城乡收入差距的实证分析。
4.2 相关数据选择与说明
本文选取的样本区间为 1993-2012 年,相关数据来自历年的《中国统计年鉴》。对相关的变量都取对数,不仅可以消除数据的异方差性;还可以在取对数之后,将之前的指数趋势变换为线性趋势、从而更好的去进行弹性分析。为了对相关数据的选择做出解释,决定赋予这些指标英文名称来进行描述。其中,IT 表示城乡收入差距,由上述分析可知,城乡收入差距有城乡居民收入差、城乡居民收入比、泰尔指数和基尼系数来作为指标进行衡量。在本文中,决定采用最常用的城乡居民收入比作为指标来测度我国城乡收入差距,其计算方法是城镇居民家庭人均可支配收入与农村居民家庭人均纯收入的比值,农村居民家庭人均纯收入为分母;用 DZ 来表示第二和第三产业的总比重,关于这各指标的选取采用第二和第三产业就业人数之合占总就业人口的比重;CT 表示城乡人力资本投资差异,由于城乡人力资本投资收益率难以去衡量和量化,所以关于该城乡人力资本投资差异的公式中忽略掉城乡人力资本投资收益率的部分,只用城市和乡村人力资本投资各部分的总量之比来衡量,得到的关于城乡人力资本投资差异的计算方法为:
城市人均人力资本投资与农村人均人力资本投资的比值,农村人均人力资本投资为分母。在本文的数据中,由于人力迁移投资方面的数据得到存在困难并且该方面在人力资本投资中占的比重不太大,故本文中关于城乡人力资本投资用城乡文教娱乐和医疗保健之和来衡量。上述所需要的相关数据如下表 4.1.
4.3 实证分析结果与结论
4.3.1 单位根检验
因为我们在经济领域中所获得的很多时间序列观测值都不是在平稳的过程中产生的,即为非平稳的时间序列,该序列的均值或自协方差函数会随着时间而改变。所以,常用的回归方法并不适用。在这里首先将运用 ADF 单位根检验对相关变量的平稳性进行检验。在该检验中,最佳滞后阶数是根据 SchwarzInformation Criterion(SIC)准则确定,得出的 SIC 值越小,那么相应的滞后阶数带来的效果就越好。在单位根检验的检验形式为(C,T,L),括号中的 C 代表常数项,T 代表时间趋势项、L 代表滞后阶数。例如,在下表中出现的(C,0,0)代表的含义是有常数项、无时间趋势项并且滞后阶数为 0;(C,0,1)代表的含义是有常数项、无时间趋势项并且滞后阶数为 1;(C,T,1)代表的含义是有常数项、有时间趋势项并且滞后阶数为 1.具体结果见下表 4.3.
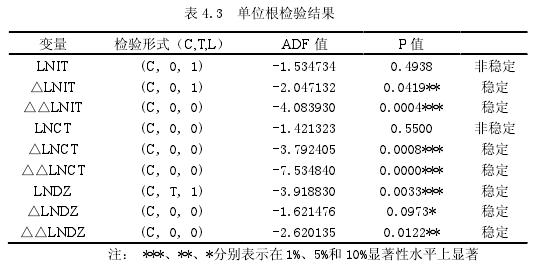
从表中的检验结果看出,第二三产业总比重(DZ),城乡收入差距(IT),城乡人力资本投资差异(CT)的变化率都是二阶单整的单位根检验过程。其中,LNIT 和 LNCT 接受数列非平稳的假设,但是经过一阶差分和二阶差分之后,LNIT、LNCT 和 LNDZ 都拒绝数列非平稳的原假设。所以,上述变量数据符合相关协整分析所需要的条件,可以对其进行协整检验。
4.3.2 协整检验
(1)确定协整阶数
在进行 ADF 检验确定上述变量是平稳之后,然后进行协整检验。要进行协整检验便需要检验这些变量之间是否存在协整关系,本文采用的是 Johansen 协整检验的方法对协整关系进行检验,从而确定变量之间的相关关系。因为为了确定协整关系统计上的可信度,需要确定最佳的协整滞后阶数。所以,在对这些变量做Johansen协整检验之前,必须先确定变量的最佳滞后阶数。确定水平VAR 模型的最佳滞后阶数的方法是:遵循从一般到特殊的原则,先从较大的滞后阶数开始计算测试,根据所得到的 LR 值、FPE 值、AIC 值、SC 值、HQ 值等来确定相应的最佳滞后阶数。如上表 4.4 的检验结果,在 5%的显着性水平上,LR 值、FPE 值、AIC 值、SC 值和 HQ 值都拒绝原假设。因此变量的最佳滞后阶数均为 L=1.
(2)协整向量个数 r 的检验
根据上表 4.4 中的检验结果,确定出的最佳滞后阶数为 L=1,然后对变量进行 Johansen 协整检验。从下表 4.5 中得到的结果,看出在 1%显着水平上,轨迹统计值为 35.94129,因为 35.94129>35.45817,所以应该拒绝没有协整关系(r=0)的原假设。说明在 1%的显着性水平上,拟检验的变量存在一阶协整关系,并且接受最多一个(r=1)和最多两个(r=2)的原假设。根据最多一个(r=1)的原假设也是接受的,据此可以得出在 1%的显着性水平下变量有且仅有一个协整关系的结果。
(3)协整方程
由上面的 Johansen 协整检验结果可以得出这些变量之间只有一个协整关系,其表达式如下,标准化协整向量为(1.0000,-0.716714,-0.381415,C),这些变量之间的协整方程为(各系数下面的括号中的数值为标准差):

上述协整方程各变量的估计系数都通过显着性检验,故在 1993-2012 年,我国的城乡居民收入差距、第二三产业结构总比重、城乡人力资本投资差异 3 个变量之间存在长期均衡的协整关系。并且从长期来看,第二三产业结构总比重、城乡人力资本投资差异与城乡居民收入差距呈正相关关系。其中,正相关程度是城乡人力资本投资差异比第二三产业结构总比重要强。
从回归结果来看,城乡人力资本投资差异对城乡收入差距的相关系数是0.716714,城乡人力资本投资差异每增加一个百分点都会导致城乡收入差距0.716714%.根据第二部分中的研究分析,城乡二元体制引起城乡经济资源配置不均衡和城乡人力资本投资收益的二元性,城市比农村享有更多的资源,更好的经济资源配置使得人力资本投资的收益率城市也是高于农村的,并且由于农村外溢人力资本投资的浪费,都会导致城乡人力资本投资差异的扩大,从而引起城乡收入差距的扩大,是符合理论分析的。
另外一个结果是,第二三产业结构总比重对城乡收入差距的相关系数是0.381415,第二三产业结构总比重每增加一个百分点都会导致城乡收入差距扩大0.381415%.根据第二部分中的研究分析,高劳动参与率会影响到城乡收入差距的变化。适龄劳动人口的比重过大,会引起农村剩余劳动力的转移。在转移的过程中,由于对农业研究投入不足和重工业优先的政策倾斜用农业部门的发展来弥补非农业部门的发展,导致城乡收入差距的不断扩大;并且因为分割城乡劳动力市场户籍制度的存在和农村劳动力流向城市低层次产业同样会造成城乡收入差距的不断拉大,同样符合理论分析。由此可见,两个变量之间的协整关系均与理论分析一致。
4.3.3 误差修正模型(VECM)及其诊断检验
由上述协整检验结果证明这些变量是存在长期均衡的协整关系,并且本文主要检验城乡收入差距和第二三产业总比重、城乡人力资本投资差异的关系。因此,给出关于 LNIT 和 LNCT、LNDZ 的误差修正模型,相关的误差修正模型估计结果见下表 4.6.
接下来应该对该 VECM 模型分别进行稳定性、自相关性、异方差性以及正态分布检验。根据图 4-1 中的结果,很明显看出 VECM 的模型设定的单位根都落在单位圆以内(其中有两个根重合都为 1.000000),证明该模型中的各变量之间存在着稳定的线性关系,该 VECM 模型是稳定的,可以进行下面的脉冲检验。
进行 LM 自相关的检验结果是:LM1=5.891427,P 值=0.7507;LM2=11.22355,P值=0.2607,证明该 VECM 模型并不存在自相关性,可以继续进行其他检验;运用 White 检验模型对该模型是否存在异方差进行检验,所得的结果为:χ2 值=44.10125,P 值=0.6333,该结果证明其不存在异方差;接下来判断该模型是否符合正态分布,通过运用联合正态性检验,得到的结果为:Jarque-Bera 值=7.680538,P 值=0.2625,证明其符合正态分布。
根据上述各类检验结果,能够判断出 VECM 模型不存在设定偏差,并且稳定性十分显着。接下来可以对该 VECM 模型分别进行格兰杰因果关系和脉冲响应分析。
4.3.4 Granger 因果关系检验
上述 VECM 模型经过检验证明 LNIT,LNCT,LNDZ 三个变量之间存在长期的协整关系,但是却不能告诉我们城乡收入差距、第二三产业总比重和城乡人力资本投资差异的因果关系。所以,对模型中的 LNIT,LNCT,LNDZ 三个变量进行 Granger 因果关系检验。
检验结果如上表 4.7,在 2 阶滞后的大条件下,10%显着性水平上,城乡人力资本投资差异对城乡居民收入差距是拒绝原假设,即拒绝城乡人力资本投资差异是城乡收入差距的的原假设,所有城乡人力资本投资差异对城乡收入差距具有单向 Granger 影响;同样的结果也表明出在 2 阶滞后和 10%显着性水平上,第二三产业所占总比重对城乡居民收入差距是拒绝原假设,第二三产业所占总比重对城乡居民收入差距也具有单向 Granger 影响。结果说明城乡收入差距在长期受到第二三产业结构的变动和城乡人力资本投资差异的共同作用。
4.3.5 脉冲响应函数
由于 VECM 模型所得出的结论不能很好地去解释估计系数,并且上述的实证过程中已经通过了协整检验和 Granger 因果检验,所以本文将通过脉冲响应函数来得出结论。图 4-2 中第一个图是以误差修正模型为基础,得到的广义脉冲响应函数曲线。其中,在广义脉冲响应函数中,横轴表示的是滞后阶数,纵轴表示的是城乡居民收入差距受城乡人力资本投资差异的响应程度。第二个图横轴表示的是滞后阶数,纵轴表示的是城乡居民收入差距受第二三产业总比重的响应程度。
因为伴随着时间不断的往后推移,上述的内生变量在被序列冲击时所受影响会逐渐变小,说明对应的 VECM 模型是个十分稳定的系统。根据下面两张图能够判断出,以 14 年为界,广义脉冲响应函数趋于平稳,并且收敛于一个特定值。
依据上图 4.2 的广义脉冲响应函数曲线左边的图可以看出,在 1-14 年的滞后期内,城乡收入差距在受到城乡人力资本投资差异的冲击后,所得出的冲击效应为正,即城乡人力资本投资差异的提高导致城乡收入差距扩大。在滞后期为14 年以后的时期内,城乡人力资本投资差异对城乡收入差距的冲击逐渐趋于稳定;从上图 4-2 右边的图可以看出,在 1-14 年的滞后期内,城乡收入差距在受到第二三产业总比重变动的冲击后,所得出的冲击效应为负,即第二三产业总比重的上升会导致城乡收入差距缩小。这是由于产业结构的变动在当期会导致城乡收入差距的扩大,但是产业结构的优化在滞后期内是会使城乡收入差距缩小。大量劳动力从第一产业转向第二和第三产业的时候,是基于不同产业的相对收入和劳动生产率的差异,随着不同产业中的投资报酬差异逐渐缩小的时候,产业结构渐于稳定的时候,会促使各产业之间的相对收入差距缩小。可以进一步的促进城乡经济协调发展,提高农村的相对收入,使城乡收入水平的差距能够慢慢缩小。
所以,产业结构的优化和人力资本投资差异的变小对滞后期中的城乡收入差距是起着缩小的作用的。





