
一、引言
1952 年,在 Markowitz 的 《投资组合选择》 一文中,创造性的对投资组合均值—方差模型概念进行了相应的论述,这是现代投资理论发展史上的一个重要里程碑式成果,为现代证券投资相关理论的出现和完善提供了基础的理论支持。以此为基础,Sharp 等人于上世纪六十年代首次提出了资本定价模型。而当前阶段,CAPM 模型已经广泛的应用于现代金融理论研究中来。
上海证券交易所诞生之后,我国的股票市场历经数十年发展而逐步趋于完善,逐渐成为一个有效率的市场,特别是金融行业股票发展势头良好,但是相对于西方发达国家来说,市场的完善程度还有着较大的提升空间,因此我们完全有理由可以认为中国股市仍然处于初期阶段,各方面仍然有着大量的不足之处。
在本文的研究中,主要是通过对国外先进的理论研究成果的借鉴和吸收,以 CAPM 模型对沪市 A 股市场金融行业股票数据有效性进行实证分析,从而得出有效数据来支撑资产定价理论,为我国股票市场有效性的提升提供支持。
二、文献综述
Sharp 等人创造性的提出了 CAPM 模型之后,以西方成熟资本市场为主要研究方向的大量成熟实证分析开始大量出现。
Black、Jensen 等人重点分析了纽约证券交易所在 1994 年前后的股票数据资料,通过构建统计噪音模型的方式,重点论述了资产定价模型的有效性。在他们的研究成果中完全意义上的佐证了零 β 资本资产定价模型,实际上其主要的研究成果所提供的 β 值可以有效的为绝大部分投资组合的平均收益率差异提供支持。但是在他们的研究中同样也证明了非系统风险同样会对最终的资产收益率水平产生客观的影响。
Fama 等人的研究成就主要是通过多元线性回归模型来验证 CAPM模型在实际应用过程中的有效性,他们的研究证明了平均收益和 β 呈线性关系,这和该模型的理论是相符合的,而系统风险在这一过程中并不能够得到有效的弥补,也就是说 σ 并不能直接的影响平均收益水平。除此之外,在上世纪八十年代至今,各种负面的验证结果层出不穷,值得我们给予更多的关注。
在 Reinganum、Lakonishok ( 1981) 等人的研究成果中发现平均股票收益和风险在二十世纪七十年代之后所产生的金融数据之中的关联度水平逐步降低并趋于消失; 而在 Banz ( 1977) 的研究成果中同样也说明了市场盈利水平高的公司的组合样本收益并不能真正的高于低市场盈利率公司。
在 Fama 等人针对 CAPM 所进行的一系列深入分析中,他们通过实证分析的方式验证了两个数据之间的影响能力,认为并不像传统观念中两者之间存在着紧密的联系。而这种情况可观存在的主要原因是因为他们对之前一系列的 CAPM 异常现象研究结果进行了归纳总结。同样的,在 Fama 和 French 的研究中也同样论证了 CAPM 理论对近五十年的平均股票收益的解释能力不足。
综上,针对 CAPM 模型所进行的实证分析可以根据内容的差异分为两个历史阶段。早期的研究主要是从方法论角度展开的; 而后期的研究则主要是将目光集中于大量的异常现象上。
我国国内针对这一问题所进行的研究主要将方向集中于国内股市是否有条件应用 CAPM 方面,所进行的研究对于 CAPM 的推广起到了重要的推动作用。
施东辉针对 CAPM 进行了大量的实证分析,选择 1993 年 - 1996 年上交所的五十种股票作为分析对象,论述了系统性风险和预期收益之间具有明显负相关的观点。
杨朝军、邢靖所进行的研究主要是通过对上海股票交易市场的分析展开的,认为该市场本身尚未具备推进 CAPM 的条件,这是因为该市场中的股票定价受到大量的非市场因素影响。
吴颖玲的研究成果中,验证了孙鹏飞等人在 《资本资产定价模型在中国股市的拟合程度分析》,中所提出的观点,认为我国当前股票市场中的系统风险并不能完全意义上的决定收益水平,可流通股票的占比等一系列因素都能够对这一指标产生明显的影响,而且不同要素的影响能力在不同时期也是有着明显的差异的。
通过对我国国内大量专家学者针对 CAPM 的实证分析结果中我们并不能简单的认为 CAPM 是否适应中国国内市场,但是当前的主流观点认为 CAPM 在中国股市的应用尚且缺乏必要的环境基础。
三、实证检验
1、模型简介
作为资本市场中的一种常见均衡模型,资本资产定价模型广泛的应用于风险—收益计算、证券风险评估等领域中。该模型本身所具有的能够可以计量检验的特点为其广泛应用提供了必要的支持,同时本身能够在尚不确定条件的环境下的有效应用能力,为投资者最大效益计算过程中的大量应用也奠定了必要的基础。
正如我们所知道的,当前技术条件下的所有模型都必然要对繁杂的外部环境进行归纳提炼才能提出,从而找出最重要的因素,因此我们在实际的研究过程中必须对外部环境进行相应的简化处理,同时提供相对应的假设条件。CAPM 模型在实际的应用过程中,具体的假设条件应包括如下几方面的内容: ①不存在个人所得税及交易成本; ②资产可无限分割并都可交易; ③投资者不可通过自身的买卖行为对股票价格造成影响; ④投资者仅对投资组合收益率的期望值和标准差考虑,对组合决策的必要投入元素具有一致的期望; ⑤无限卖空不受限制; ⑥可以以无风险利率不受限制地借款和贷款。
按照上述假设条件,我们可以将 CAPM 模型简单的表达为:
E ( Ri) = Rf + βi [E ( Rm) - Rf]
在上式中,E ( Ri) 代表了当前的股票期望收益率水平; 而 Rf 则代表了无风险收益率水平; 其中的 E ( RM) 代表了市场组合的期望收益率水平; 而 βi 则是研究对象的股票收益率与市场指数收益率的协方差与市场收益率方差的比值,这一数据同样用于评估市场风险的总体水平。
根据 CAPM 的相关设定我们可以知道,某一特定资产的期望报酬率水平受到如下三方面要素的共同影响而最终确定: 货币的纯粹时间值、承担风险的具体回报情况、系统风险。这三者分别可以通过无风险利率Rf 和 βi 来计量,这是判定系统风险基本水平的重要数据。
2、数据选取的理由与来源
2012 年中国股市起起落落,宏观形势颇为复杂国内经济走势一直下滑直到年底才有复苏迹象,全年最高点为 3 月份的 2478 点,最低点为12 月份的 1949 点,全年窄幅震荡。2012 年以银行、保险、券商为主的金融行业整体作为股市的主力军,继续领跑市场。银行板块走出前高后高中间低的格局,12 月也是大盘上涨的最大的主力军,显示市场对蓝筹板块的认同,最低至 1509 点,最高至 1793 点。保险板块全年基本走强趋势,年末反弹,最高点 777 点,最低点 579 点。券商信托板块,由于利好消息,全年基本强势走高,12 月份也是大盘上涨的主力军之一,最高至 56358 点,最低至 45156 点。从以上一系列数据可以看出金融行业股票是我国优质股票的代表,区别于一般沪市 A 股具有特殊性,本文希望通过分析金融行业股票数据来检验 CAPM 模型是否适用于分析沪市A 股金融行业股票。
本文以沪市 A 股市场金融行业股票为研究对象,选择了一共 30 只股票,可以体现样本的普遍适用性。同时为了体现近年来沪市 A 股金融行业股票市场行情的最新变化,使检验具有现实意义,本文选取2011 年6 月 15 日至 2014 年 3 月 31 日的 485 个数据作为本研究的主要研究样本数据,同时为了保证研究结果的有效性,采用周数据作为样本数据的方式来提升样本数据的总体数量水平。
正如我们所知道的,CAPM 模型在实际的应用过程中客观上要求市场组合必须能够和市场上的全部资产之间保持最高相关性水平,而这种假设在真实的市场中基本上是不存在的,基于这一情况,在本文的研究中选取上海证券交易所 A 股指数的收益率作为研究中市场组合的收益率。上证 A 股指数包含了上海股票市场的具有代表性的股票,反映市场的总体态势,具有广泛的代表性。而无风险利率,所有研究中涉及到的数据全部采用当年银行一年定期存款利率,同时按照复利计算的模式将其进行周利率转化。 ( 本文采用的数据来自于瑞思数据库。)
3、检验过程
诚如上文中所介绍的,我们可以以如下公式简化的表达 CAPM:
E ( Ri) = Rf + βi [E ( Rm) - Rf]
通过收益计算来求得个股和上证 A 股指数的周收益率,Pit 为第 i 只股票在 t 周的收盘价格,Pi ( t -1) 是第 i 只股票在 ( t -1) 周的收盘价格。
( 1) 单只股票 β 系数的估算
按照如下某型对所获得的数据进行回归分析:
Rmt 为上证 A 股指数在 t 周的收益率,Ri 是第 i 只股票在第 t 周的收益率,βi 为此模型所估计的 β 值。在本文的研究过程中首先通过 excel软件对数据进行了初步的整理,然后采用当前较为流行的 EVIEWS 软件进行相应的回归分析,从而能够得到个股的 β 值。
( 2) 横截面检验
在本文的界面检验过程中,针对经过相应整理的三十只股票以及上证 A 顾指数的 β 值后,对经过回归分析的 β 值带入回归方程中进行二次计算,其方程表达式为: Ri = γo + γ1βi + εi
四、实证结果
1、样本期内沪市 A 股金融行业股票的参数方程和 β 估计值。 ( 见表一)
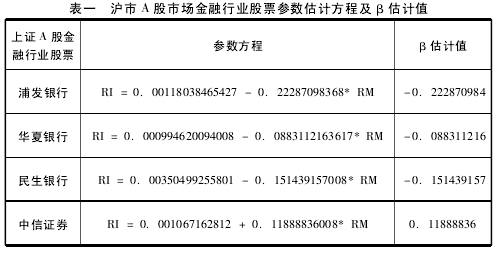
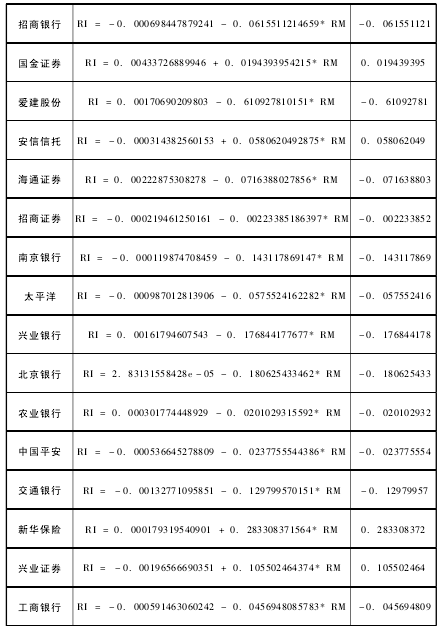

β 在本研究中主要是对系统风险进行衡量,该值和系统风险性水平之间为正相关关系,同时和报酬率水平之间也具有明显的反比例关系。
也就是 β 的大小之间关系到报酬率水平的高低。而在投资策略的选择过程中,如果投资者本身属于风险投资偏好属性,那么有若干 β 较高的股票供其选择,而反之,则可以选择一些 β 值相对较小的股票,虽然相对于前者来说整体的投资回报率水平必然偏低,但是风险也同样偏小,市场变动对其所产生的影响较小。单个证券的 β 的加权平均数构成了证券组合的 β 值。为了降低后续研究的计算强度,我们在这里首先假定目标股票市场的风险为 1,以此为基数来衡量某一证券的风险敏感水平。一般情况下,我们认为防守型证券的 β < 1,本身所蕴含的系统风险相对于外部证券市场来说明显偏低,如果市场出现回落情况,那么收益的跌幅必然会小于市场的平均收益跌幅,当然,增长情况同样具有如上规律。相反,β >1 的证券我们通常称之为进攻型证券,其风险水平明显高于所处证券市场的平均风险水平,这就导致如果市场出现明显的变动情况下,无论是收益水平还是跌落水平都必然高于市场的品均水平。β= 1 的证券,它的系统风险等同于市场风险,与整个证券市场同步。通常情况情况下市场总体跌落的情况下可以选择防守型证券,反之则需要持有进攻性证券。
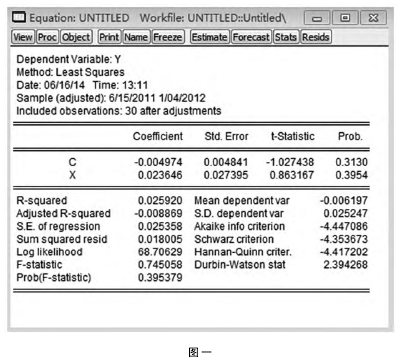
2、横截面检验实证结果回归结果为:
Ri = - 0. 00497433286274 + 0. 023646405115βi
( 0. 004841) ( 0. 863167)
R2 = 0. 025920 F = 0. 745058
通过对上述结果的简单分析我们可以发现,R2 = 0. 025920,这一数据充分证明了该模型的拟合优度水平处于较低的层次上,那么也就意味着系统风险并不能有力的解释股票预期收益水平,且呈现为不显着的正相关,这和收益—风险正相关的情况之间是完全不符的。而通过截距项以及斜率的参数计算数据 t 统计量所对应的 P 统计值进行分析我们可以发现,基本上完全大于 0. 1,在 10% 显着水平下,并能够有效的否定原有假定情况,参数估计值显着为零。又从 P ( F - statistic) 为 0.395379 可知,模型整体的显着性不高。
五、结论
CAPM 模型是资本市场上一个重要的金融资产定价模型,简单而又操作性强,在投资风险分析、资产定价以及股票收益预测中起着重要作用。首先,CAPM 模型仅仅是一种简单总结证券市场的研究方法,必然要求有相对严格的假定为前提。其次,CAPM 理论忽略了其他因素对单个收益率的影响,将所有的系统风险都归咎于一个 ( 相对风险) 因素之中。即使是在已经相对成熟的证券市场中,面对这些条件和假设也同样不能够完全意义上的满足假定条件。基于上述情况,无法提供完全意义上满足假定条件的环境下,CAPM 的应用就必然存在一定的差异,也就是说并不能够符合全部证券市场。
从上世纪九十年代开始,我国国内的大量专家学者就已经开始针对CAPM 进行了大量的研究,并结合我国的证券市场实际情况展开了实证分析。实际上,CAPM 模型中认为系统风险和非系统风险共同构成了市场风险。而其中的非系统风险的消除可以通过投资组合的方式来实现。
而系统风险则无法通过这一方式加以消除。我国当前阶段的证券市场,尤其是股票市场中,整体风险水平偏高是不争的事实,这种情况的客观存在不仅仅由于大量的自然因素的影响,同样还有着国家政策引导、投机问题严重等问题的客观干扰。这实际上增加了系统风险的比重。而为了有效的规避系统风险,我国证券市场中强烈要求增加股指期货。这种典型的金融衍生工具对于保证我国股票市场的长期稳定、健康发展是具有一定的积极意义的。
从本文上述实证分析中得出结论: CAPM 模型在我国沪市 A 股金融行业市场上无效。这主要归咎于以下几点原因。首先在我国证券市场发展相对较晚的情况下,沪市 A 股金融行业股票虽然走势较好但市场还不成熟,并不能完全意义上的提供有效市场环境,尤其是政策影响严重、短期短线投机多于长期持有、投资理性不足等问题的长期存在,更是严重的增加了市场的盲目性。其次,股票市场的效率很低,股票市场的信息机制与价格机制对资源的引导与配置能力还处于非常薄弱的水平之上: 噪声交易对市场的影响能力极大,严重的干扰了市场的有效性。基于上述情况,当前阶段我们想通过 CAPM 模型对沪市 A 股金融行业股票市场风险—收益率二者关系进行预测并指导投资决策是不可行的。
CAPM 模型中的 β 并不能有效的反映出所有影响股票收益率水平的要素,两者之间并不存在明显的相关性。同时股票的收益率解释变量中,β 比例也同样偏低,如股本规模、净资产收益率和成交量之类的要素的影响能力都明显的大于 β。因此,在此后的学术研究和实际应用中我们还需要不断改进 CAPM 模型使之不断趋于完善。
参考文献:
[1] Stattman,Deniss,1980,Book values and stock returns,The ChicagoMBA: A Journal of Selected Papers 4. 25 - 45
[2] Edwin J. Elton,Martin J. Gruber,Stephen J. Brown,William N.Geotzmann. Modern Portfolio Theory and Investment Analysis,2011
[3] Reinganum,Marc R ,1981,A new empirical perspective on theCAPM,Journal of Financial and Quantitative Analysis 16,439 - 462
[4] 林少宫,李楚霖. 简明经济统计与计量经济 [M]. 上海: 上海人民出版社,1996.
[5] 陈柳钦,曾庆文. CAPM 理论在我国证券市场中的应用及改进 [J ] . 中国机电工业,2003 ( 12) .





