
针对第 1 种算法设计,以往研究认为下单速度越快,股价波动的风险越小,但冲击成本就越大。Bertsimas 和 Lo[1]假定投资者有单位的股票要在 T时刻前变现,给定股价波动风险的约束,求解了最小化总执行成本的变现策略。 在静态策略的基础上,Almgren 和 Chriss[2]研究了股价变动因素对变现策略的影响。 类似地Obizhaeva 和 Wang[3]在假定市场冲击为线性且价格冲击随时间呈现指数衰退的条件下求解了最优变现策略。
针对第 2 种算法设计,Alfonsi[4]等研究了限价指令簿( LOB) 弹性模型的最优执行策略,将限价单数量和买卖价差为自变量的 LOB 弹性模型与市价单对 LOB 冲击模型相结合,求解了相应的变现策略。
在以上最优变现策略的研究中,冲击成本函数的构造是一个关键点。 Gatheral[5]综合考虑了线性、指数和幂函数三种衰减方式,通过实证研究发现非线性的冲击函数与数据较为符合。 Almgren[6]估计了非线性冲击函数的参数,美国市场数据表明价格冲击约为交易速率的 0. 6 次幂函数。
本文将研究基于限价指令簿的最优变现策略,而不考虑拆单方式。 考虑投资者试图通过限价指令在 T 时刻前变现份额的头寸,报价越高,则成交概率越低,但收益越高。 投资者的目标是选择最优报价机制使预期收益最大。 在限价指令下,风险主要体现为可能无法在 T 时刻前变现要求的头寸,价格波动和冲击成本的影响都不存在。 Guéant[7]等和Bayraktar 和 Ludkovski[8]在研究限价指令簿的清算策略中采用市场交易密度函数来刻画市场流动性,假定投资者通过选择高于一档买价的价差来控制交易频率。 本文的研究将采用市场交易密度函数的方法讨论限价指令簿下最优变现策略,在现有理论基础上将波动率引入模型,一方面,将卖价报价高一档买价的价差标准化,解决了绝对价格的不同带来的差异,另一方面也体现出,随着股价波动率的增大,卖价被“触及”的可能性增加,相同价差的成交的概率也可能提高。 本文将分为模型创建、数值求解最优变现策略、蒙特卡洛模拟交易曲线以及参数的敏感性分析等几部分进行阐释。
1 模 型定义
概率空间( Ω,F,P) ,滤波( Ft)t≥0服从常用条件。 假设所有随机变量和随机过程都基于该概率空间。 股价服从带漂浮率的布朗运动,定义如下:dSt= μdt + σdWt其中: St为第一档买价,μ 为漂移率,σ 为波动率,Wt服从标准正态分布。
为避免冲击成本,投资者采用下限单的报价方式,q0为其需要变现的股票头寸。 令 Saskt为卖价,s= Saskt- St为卖价高于一档买价的价差。 那么投资者的卖出挂单是否能够顺利成交,就取决于是否存在足够多的市价买单或是愿意购买的“激进的买单”. 因此,投资者的最优变现策略问题就归结为研究如何选择最优的基于一档买价的卖出限价。 本文将针对不同的约束条件对这一问题进行探讨。
1. 1 市场交易密度函数
假定成交以单位数量进行( 单位数量为 1,或某一整数) ,则挂单的状态分为两种: 成交、未成交并继续留在限价订单簿中。 可使用伯努力函数刻画挂单的状态,设为 Λ( s) 成交的概率密度,并定义:

其中: s 为高于一档买价的价差,λ 和 κ 是用来衡量流动性的两个参数,与股票一一对应,在实际运用中用数据校准得出。 显然,密度函数与价差负相关,价差越低则卖价越便宜,挂单的执行速度越快。
1. 2 最大化期望收益目标
函数Nt为 t 时刻前已成交的挂单数量,Nt与 Λ( s)密切相关。 则 t 时的剩余持仓量为 qt= q0- Nt. 因此,投资者收益 Xt的动态形式为:
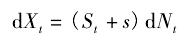
假设投资者需要在 T 时刻内卖出所有的股票,目标是最大化 T 时刻的收益,那么构造如下效用最大化目标函数:
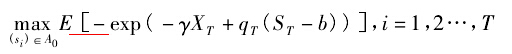
其中: A 为价差可选集合,γ 为绝对风险规避系数,qγ为在 T 时刻尚未成交的股票,ST为在 T 时刻的市价,b 为清算剩余持仓所需的单位成本。 不难发现,效用函数为收益 XT的增函数,T 时刻剩余持仓qT的减函数。 最大化目标函数就是用来求解价差s,即投资者在每一个时刻新提交的卖单价格高于一档买价的价差。 目标函数的求解可以使用 Hamil-ton - Jacobi - Bellman 方程的方法。
1. 3 Hamilton - Jacobi - Bellman
方程转换Hamilton - Jacobi - Bellman( 以下简称 HJB) 方程是用来解决最优控制问题的偏微分方程,它的解是给出了控制系统的最优成本的价值方程。 将 HJB方程引入最优化方程的求解,假设方程 u 是一个未知的价值方程,并且满足:
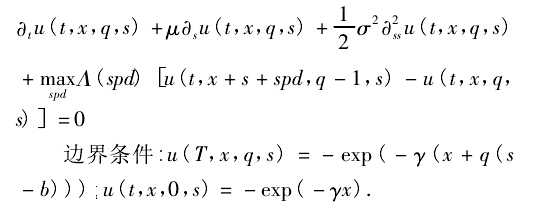
引入一组常微分方程,则 HJB 的价值方程可用这一组常微分方程来写出。 定义( Wq)q∈N为一组常微分方程满足:
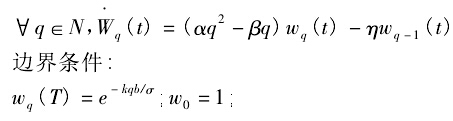


2 数值求解。
2. 1 最优限价单报价。
HJB 方程给出了在不同条件下的最优报价。 图1( A) 描述了给定时间内( 1 ~ 5 min) 卖出相应数量股票( 横坐标,1 至 5 份额) 的最优价差情况( 纵坐标) . 可以发现,股票待交易数量越多,价差越小,是为了保证更快的执行; 随着清算时间的变短,价差也在变小,也是为了在给定时间内卖出更多的股票。 图 1 中可以发现,当时间只有 1 min,而仍然持有 5 份额的股票时,模型隐含的最优价差为零值;而当持有超过 5 份额以上的股票时,模型给出的最优价差将为负值( 图 1 中未显示) ,这在现实中是不可能的,然而由于在模型中并未对价差的符号做出限制,因此价差为负值时我们将它视为即时市价交易指令。 负价差的出现与指令簿密度函数系数γ、λ,股票波动率 σ,未成交的成本 b 有关。 我们可以将成本 b 当作未及时成交的惩罚,当 b 很大时,价差是容易出现负值的; 当投资者是对风险嫉妒厌恶的,或者股票的波动率很大时,投资者都急于清仓,甚至是不惜成本的,所以价差在模型中也会变成负值。
图 1( B) 描述了在 5 min 内( 横坐标 300 s) 分别按限价单卖出 1 到 5 份额股票的各个交易时刻的报价差( 纵坐标) . 在零时刻,持仓量越小,报价越高,投资者不急于立刻成交,想要在更高的价位上卖出以得到更高的回报; 而持仓越多的投资者会降低报价,减少不能及时成交的风险。 从时间的角度而言,价差最终都会趋于一个定值:
 。
。

2. 2 蒙特卡洛模拟与交易曲线
根据 HJB 模型可以求解最大化效用函数的报价,本部分将对这一报价的交易结果进行检验。 由于缺乏可供使用的限价单数据,本文采用蒙特卡洛方法模拟市场情况和报价路径,求得交易的期望值。
图 2( A) 给出了一次随机模拟的交易情况,描述了投资者在零时刻有 8 份额的持仓,如何在 5min 内变现的交易曲线。 我们可以看出交易成跳跃式,并在 240 s 左右就已经完全变现。 一方面由于股票的价格是随机波动的,另一方面最优报价的成交情况也是服从一定概率分布的,所以需要根据蒙特卡洛模拟得出 N 次交易的均值,才能描绘出相对连续的交易曲线。 图 2( A) 为在 5 min 内,不同的持仓量下按限价单报价方式的交易曲线。
Almgren 和 Chriss 表明,在不考虑价格波动风险的情况下,最优市价交易策略是按均匀速率交易,对应的交易曲线应为一条直线。 与此相比,基于限价单的最优报价而形成的交易曲线偏凹形,即在开始交易得更快,并逐渐趋于平缓。 这也是由于我们考虑了股票的波动风险以及无法及时变现的风险。 另外,在 T 时刻,q 并没有减少到 0,这是因为未完全变现的惩罚 b 数值不够大,假如 b 趋向正无穷,那么在 T 时刻前将会完全变现。

2. 3 敏感性分析
本节讨论各参数对最优价差的影响。 基本参数设定为 5 min 内分别变现 1 到 5 份额股票,最优价差结果见图 3.

测试的参数分为 3 类:
1) 描述股票性质的 μ,σ漂浮率 μ 描述的是股票的预期的涨跌情况,μ越大,股票有升值预期,此时的报价会偏高,因为交易越晚,可能收益越高。 波动率 σ 的影响则分为 2部分: 一方面,波动增大意味着在给定报价水平上成交的概率变大,从图 3 可以看出,当待交易数量较少( 即变现压力较小) 时,σ 越大,价差越大; 另一方面,波动率也代表了交易不确定性,所以当待变现数量较多( 图 3 中数量大于 3 份额) 时,波动率越大,报价越低,投资者偏向迅速成交,及时变现。
2) 密度函数参数 κλ成交密度函数定义为: Λ( s) = λe- κs / σλ > 0,κ> 0. 所以 κ 与 Λ( s) 成反比,λ 与 Λ( s) 成正比。 因此,κ 越大,λ 越小,相同价差下成交的概率越小,为保证及时变现,只能降低报价。
3) 效用函数参数 γ,b绝对厌恶系数 γ 既与股票价格波动风险有关,又与未执行风险相关。 所以当越大,投资者更厌恶风险,就会选择更快地卖出股票,降低报价。 b 作为未变现的惩罚,在图 3 中影响不大,是因为 b 已经足够大使得交易在 T 时刻前完全执行。
3 结 语
本文就限价单的报价策略展开了研究,目的是使得期望收益最大化的同时又尽量保证交易的完全执行。 本文以指数函数刻画了市场成交密度函数,探讨了基于限价交易的最优报价策略。 该策略适用于希望锁定成交价格并减少市场冲击的投资者,在其他算法交易( 如 VWAP 策略等) 拆单后的小区间的限价交易中也有应用。
在给定的输入变量( 1) 初始时刻待交易数量q0( 2) 交易时间 T,模型参数( 3) 描述成交概率的参数 λ 和 κ( 4) 绝对风险规避系数 γ( 5) 清算剩余持仓所需的单位成本 b ( 6) 股票漂移率 μ 和波动率 σ,利用 HJB 方程能够将最优策略的求解问题转换为一组常微分方程,就可以求出指令交易中的高于一档买价的卖价价差,进而投资者可以据此卖价下限价单。 使用数值方法可以获得数值解,发现当持仓越高或交易时间越短时,报价越接近一档买价; 当模型给出的报价价差在贴近期末变为负值时,需要转化为市价交易信号。 另外,本文结合蒙特卡罗模拟方法模拟市场交易曲线并讨论了各个参数的变化对结果的影响。 将股价波动率加入市场成交密度函数,既避免了绝对价格的不同带来的影响,又考虑了股价波动幅度的增大可能提高给定限价卖单成交的概率。
目前国内外的限价单策略研究还刚刚起步,最优执行策略的研究在理论和实践中都存在明显的价值。 在将来的研究方向中,一方面可以寻找其他的密度函数方程来刻画市场深度,另一方面,从挂单数量角度考虑,当挂单过多时,也会给市场以反向的信号,这时投资者应该寻求适当的挂单数量。
参考文献:
[1] BERTSIMAS D,LO A W. Optimal control of execution costs[J]. Journal of Financial Markets,1998,1( 1) : 1 -50.
[2] ALMGREN R,CHRISS N. Optimal execution of portfolio trans-actions[J]. Journal of Risk,2001( 4) : 1 - 46.
[3] OBIZHAEVA A,WANG J. Optimal trading strategy and supply/demand dynamics[J]. Journal of Financial Markets,2013,16( 1) : 1 -32.
[4] ALFONSI A,FRUHT A,SCHIED A. Optimal Execution Strate-gies in Limit Order Books with General Functions[J]. Quantita-tive Finance,2010,10( 2) : 143 - 157.
[5] GATHERAL J. No - dynamic - arbitrage and market impact[J]. Quantitative Finance,2010,10( 7) : 749 -759.
[6] ALMGREN R,THUM C,HAUPTMANN E,et al. Direct esti-mation of equity market impact[J]. Risk,2005( 5) : 1 - 25.
[7] GUEANT O,LEHALLE C A,TAPIA J F. Optimal portfolio liq-uidation with limit orders[J]. SIAM Journal on Financial Mathe-matics,2012,30( 1) : 740 - 764.
[8] BAYRAKTAR E,LUDKOVSKI M. Liquidation in limit orderbooks with controlled intensity[J]. Mathematical Finance,2012( 6) : 1 -5.





