
一、引言
自从 1982 年邓聚龙教授提出灰色系统理论以来,灰色预测模型在许多领域得到了广泛应用。它以“部分信息已知,部分信息未知”的小样本、贫信息以及不确定性系统为研究对象,主要通过对“部分”已知信息生成、开发以及提取有价值的信息来实现对系统运行行为的正确的认识和有效控制。另外,此方法并不建立在任何假设基础上。因此,许多的研究工作者对于动态微分方程模型 GM(1,1)进行了广泛的研究,为了提高模型预测的精确度,提出了一些改进的灰色模型。
国内学者对股票市场进行了大量的研究,李国平(2005)在寻找短点的最优组合作为灰色微分方程的背景值时,研究发现传统的 GM(1,1)模型采用均值作为灰色微分方程的背景值与实际值之间存在很大的误差,所以为了提高模型预测的精确度,他提出了一种运用黄金分割方法对传统的 GM(1,1)模型进行了改进,经过实证分析得出该方法在预测短期数据时是非常有效的。
另外,李东(2003)将灰色系统运用于股市,建立了传统的 GM(1,1)模型,通过上证综合指数和深圳综合指数的模拟与预测,得到了比较理想的结果,也反映了该模型的实际应用价值。
同时,该模型的应用领域不仅仅基于金融市场,俞爱斌、张世雄(2011)利用灾变式 GM(1,1)和定权聚类的方法对矿山企业历年的经济运行状况进行了定权聚类,然后根据聚类效果利用灾变式 GM(1,1)模型对经济运行情况较差的年份进行了预测,为矿山企业减少经济损失提供了重要的依据。
近年来,随着我国期货市场的不断完善与跨越式发展,一些传统的经典模型已逐渐在期货市场崭露头角。在期货市场中,黄金和白银同为贵金属,二者之间在某一时期存在着一定的相关性,但如果用传统的价差或比值模型来寻找套利机会实际效果并不佳。原因在于,当一种套利方法为许多人所熟知时,由于大多数交易者的参与,市场会迅速的进行修正,这就是为什么目前进行价差套利或者比值套利效果不佳的主要原因。根据个人观点,套利机会一直都存在。但是所处位置的不同,就会造成结果的不同,而所处的位置,就是看待市场的观点,体现在套利交易上,就是所采用方法的不同。因此,要想通过套利进行持续盈利,对于市场结构不同品种间的观测以及方法的持续更新是必不可少的,基于以上分析,本文利用灰色灾变模型,重新估计了金银之间的相关性,寻找最佳的套利机会。
二、理论介绍
(一)灰色模型介绍
所谓的灰色系统,是指相对于一般的总体层次来说,系统内部的信息部分是未知的,只有部分已知,且系统中数据不一定满足某种特定的分布,即该系统的信息是不完全的。灰色系统理论认为,由于外部环境的不一致性或者不确定性对于系统的影响,使得系统内部具有系统整体特征的数据呈现为一种散乱的分布,但是这种分布的数据序列,在一定程度上对于系统来说具有潜在的某种内在规则。因而,对于任何随机过程来说,在某种程度上都可以看成是灰色量得。一般在实际建模中,所取数据不一样,建立的模型也不一样,即使建立同样的 GM(1,1)模型,选取不同的数据,参数 a,B 的值也不一样。因此,在选取数据样本时,根据自己原先的特定目的,从原始数据中随机抽取一个样本,基于该样本建立一个模型。这种变化正是不同情况、不同条件对系统特征的影响在模型中的反映。
定义 1 设序列X(O)=[X(O)(1),X(O)(1),…,X(O)(n)]
将 X(O)(n)取为时间轴的原点,则称 t<n 为过去,t=n 为现在,t>n 为未来。
定义 2 设序列X(O)=[X(O)
(1),X(O)(1),…,X(O)(n)]则 GM(1,1)为时间响应式的累减还原值为n 时,称 X(O)(k)为模型模拟值。
(2)当 t>n 时,称 X(O)(k)为模型预测值。
建模的主要目的是预测,为提高预测精确度,首先要保留充分高的模拟精确度,尤其是 t=n 时的模拟精确度,因此,建模数据一般应该选取为包括(n)在 X(O)内的一个等距离序列。
定义 3 设原始数据序列X(O)=[X(O)(1),X(O)(1),…,X(O)(n)]
(1)用 X(O)=[X(O)(1),X(O)(1),…,X(O)(n)]建立的 GM(1,1)模型称为全数据 GM(1,1)。
(2)用 X(O)=[X(O)(k0),X(O)(k0+1),…,X(O)(n)]建立的 GM(1,1)模型称为部分数据 GM(1,1)。
(3)设 X(O)(n+1)为最新信息,将 X(O)(n+1)置入 X(O),称用 X(O)=[X(O)(1),X(O)(1),…,X(O)(n+1)]建立的 GM(1,1)模型为新信息 GM(1,1)。
(4)置入新信息 X(O)(n+1),去掉最老信息 X(O)(1),称用 X(O)=[X(O)(2),X(O)(3),…,X(O)(n),X(O)(n+1)]建立的 GM(1,1)模型为新陈代谢GM(1,1)。
新信息模型和新陈代谢模型预测效果会比老信息模型的预测效果好,事实上,在任何系统的发展过程当中,随着时间的变化,将会不断地有一些随机扰动或者驱动因素进入系统,使得系统的发展不断受到影响。因此,用 GM(1,1)模型进行预测,精确度较高的仅仅只是数据 X(0)(n)之后的一到两个数据,一般来说,越往未来发展,GM(1,1)的预测意义就越弱。在实际运用中,必须不断考虑那些随着时间推移相继进入系统的扰动或者驱动因素,随时将每一个新得到的数据置入 X(0)中,建立新信息模型。
从预测角度来看,新陈代谢模型是最理想的模型。因为它在不断补充新信息的同时,及时的去掉了老数据,更能反映系统的特征。因此灰色预测具有所需数据较少以及预测及时的特点。
(二)灰色灾变预测模型的介绍
灰色灾变预测是给出下一个或者几个异常数值出现的异常的时刻,以及预测值的大小。
设原始序列是X=[x(1),x(2),…x(n)]
给定上限异常值(阀值)ξ,则满足 x(q(i))>ξ 的序列Xξ=[x(q(1)), x(q(2)),…, x(q(m))]
为上灾变序列。且称 Q(0)=[q(1), q(2),…,q(m)]为灾变日期序列。
对灾变日期序列 Q(0)日期序列利用 GM(1,1)模型的思路和方法进行建模预测,即累加生成列:
Q(1)=[q(1)(1), q(1)(2),…, q(1)(m)]
以及相应的模型解q(1)(k+1)=[ q(1)-b/a]*e-ab +b/aq(k+1)= q(1)(k+1) -q(1)(k)若 q(m)(m≤n)为最近一次灾变发生的日期,则 q(m+1)为下一次发生灾变的预测日期,q(m+k)为未来第 k 次发生灾变的预测日期。
(三)波动周期性分析
由历史数列:
y ={y(1),y(2),…,y(m)}
建立三阶自回归模型y(t+3) = a0+a1y (t+2)+a2y(t+1)+a3y(t)式中:(a0,a1,a2,a3)‘=(BB’)*B*Y其中,
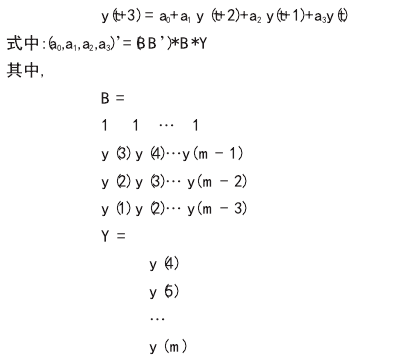
该模型的特征方程为λ3- a1λ2- a2λ - a3= 0当特征根 λ1为实数、λ2,3为复数 a+βi 和 a-βi 时,可得出tgθ0= sinθ0/cosθ0=β/a.
数列{y(t)}的周期性主要由 cosθ0t,sinθ0t 决定,所以数列的波动周期为 T=360/θ0.数列{y(t)}的近期增长规律主要由 b1λ1t决定,λ1越大,{y(t)} 的平均增长率越高。可见数列{y(t)} 的增长规律及波动周期仅与模型的特征根有关。
三、实证分析。
(一)套利可行性分析。
采用黄金(AG)和白银(AU)2012 年 5 月 10 日到 2013 年 12 月18日的日线数据进行分析,发现二者相关性良好,结果如下表一:
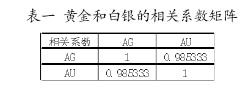
由上表可以得出黄金和白银的相关系数极大,由此可以得知黄金和白银之间的套利具有可行性。
由于黄金和白银在上期所的报价并不一致,黄金是以克为单位,而白银是以千克为单位,因此,为了便于比较,金银单位一致取为 1000 克。由于此时二者价格相差过大,因此采用比价套利的方式进行比较。期货套利的比价指的是套利的两个品种的价格比,此时,用调整后的金价去比银价。在软件中生成相应数列。
(二)灰色分析
采用相应的数据,灰色预测的特点在于其所需数据较少,过多的数据会造成较大的偏差。因而,仅仅只是截取 2013 年 11 月19 日至 2013 年 12 月 3 日的数据如下表二:
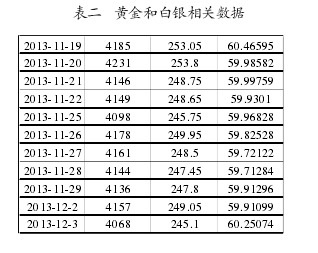
首先,运行相应程序下跌数据发生的时点,结果如下:
q =[ 2 4 6 7 8 10 ]
可以看出,原序列中第二、第七、第八、第九根 K 线下跌。
第二,进行累加生成列Q1 = [2 6 12 19 27 37 ]
进行模拟测试,拟合效果良好第三,运行相应程序,得出系数a= -0.1977 b=3.6991则模型形式为( dQ(1)/dt) 0.1977*Q(1)=3.6991模型解的相应时间函数Q(1)(k+1)= 20.7143*e-0.1977*k经过实际检验可以得出模型的小残差概率 p=1>0.95,同时c= 0.2571<0.35,故模型精确度优。
进行向后三项预测Q3 =[ 2 4 6 7 8 10 12 14 19]
即灾变发生时间为 2013 年 11 月 19 日起,第 12 个、14 个、19 个时点发生下跌,即 12 月 5 日、12 月 9 日、12 月 16 日发生下跌。
结果如下表三:
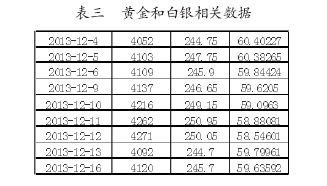
(三)周期性分析
利用以上数据进行周期分析其中,方程系数为 [1.0000 0.3589 -0.0643 -0.8731 ]
λ2,3= -0.6143 + 0.7916i && -0.6143 - 0.7916ia = -0.6143 β= - 0.7916从而解得,时间周期为 4.8753 . 大约 4 到 5 天产生价差下跌现象。
四、结语
(一)本文经过多次预测,在实际操作过程中,即在价比发生减弱的预测当天,进行空金多银的操作,效果良好,然后必须注意到,灰色预测法精确度最好的就是数列向后一到两期,因而,采用新陈代谢,不断淘汰旧数据,收入新数据的方法具有实战性。同时,灾变的定义可以进行更换,本文仅仅只是将价比下跌时点作为灾变时点,同样可以将价比上涨时点作为灾变进行预测,依据头寸方向不同进行调整。同时运用周期性分析进行交易方向的预先安排,提高胜算。
(二)本文虽然是以期货市场的黄金和白银为例来进行预测两者之间的套利关系,但是任何其他具有相关性的期货品种均可以进行套利,因此该方法可适用于其他品种的套利分析。
(三)本文在利用灰色灾变模型预测金银套利分析时,由于采用的数据样本小,因此该模型所得到得结论有待进一步的提高,但是就本文所采用的数据样本而言,其结果比较满意。
参考文献:
[1]邓聚龙。灰色系统基本方法[M].武汉:华中理工大学出版社,1987.





