摘 要: 《欧罗巴西镜录》是明末清初介绍西方笔算的一部着作.梅文鼎偶得此书,认真研读,并为之订注.通过对梅文鼎订注的探讨,并与其所着《笔算》《少广拾遗》做比对,分析梅文鼎对《欧罗巴西镜录》的理解,发现梅氏着作中吸收了《欧罗巴西镜录》中的知识,体现在梅氏对开乘方表、初商表做了扩展,在乘除法中吸收了西算的定位法.结果揭示了梅文鼎对西方数学知识的吸收过程,从新的视角探析梅文鼎的数学思想来源.
关键词: 梅文鼎; 《欧罗巴西镜录》; 《笔算》; 《少广拾遗》;
Abstract: Ouluoba Xijinglu(The Records of Europe's Western Mirror) is an important work for the introduction of western manual calculation in the late Ming or early Qing.Mei Wending, who got this book occasionally,did an intensive studies and made annotation for it.By analyzing Mei's notes and his understanding about the Ouluoba Xijinglu and comparing with his books of Bi suan(Manual calculation) and Shaoguang Shiyi( Supplement to Shaoguang),we found that Mei Wending absorbed from Ouluoba Xijinglu a lot,which were reflected in his expansion of the power table and the initial quotient table and the application of the positioning method of western arithmetic in the multiplication and pision methods by him.The study reviewed the process of Mei's absorption of Western mathematical knowledge and did an exploration for the sources of Mei's mathematical thought from a new perspective.
Keyword: Mei Wending; Ouluoba Xijinglu; Written Calculation; Shaoguang Shiyi;

《欧罗巴西镜录》(下文简称《西镜录》)不知何人所作,至今只有一册孤本传世.这个孤本由清初梅文鼎手抄并写有订注(见图1中“鼎按”),并未刊印.嘉庆五年(1800)李锐(1769-1817)在苏州购得此书.钱大昕(1728-1804)为之亲笔题跋:
图1 《欧罗巴西镜录》中梅文鼎的订注

Fig.1 Mei's Annotations in The Recordsof Europe's Western Mirror
“尚之文学于吴市得此册,中有‘鼎按’数条,盖梅勿庵先生手迹也.《西镜录》不见于《天学初函》,亦无撰人名氏,唯梅氏书中屡见之.梅所着书目中有《西镜录》订注一卷,今已失传.此殆其初稿”[1].
此事并见何元锡1《竹汀先生日记钞》,其卷一称:
“李尚之得《欧罗巴西镜录》钞本,中有‘鼎按’数条,盖勿庵手迹也.是年,焦循与李锐同寓杭州阮元官邸,焦循从李锐处转抄一本,并于书前写下题记.”[2]
《欧罗巴西镜录》能流传至今,与梅文鼎的关系最大.本文通过分析梅文鼎对《欧罗巴西镜录》的注解,考察梅氏同期着作《笔算》《少广拾遗》与《欧罗巴西镜录》之间的关系,从而揭示梅文鼎对西方数学知识的认识过程,以期进一步认识西方笔算知识对中国传统数学演变的作用和价值.
1 、《欧罗巴西镜录》中的梅文鼎订注
梅文鼎(1633-1721)一生着述甚丰,在相关着作中多次提到《西镜录》.《勿庵历算书目》记有“《西镜录》订注”一卷.《勿庵历算书目》共列名目八十八条,内中属于天文历法有六十二种,其中仅有数种单独付梓,一部分失传,一部分被后人汇刻于梅氏丛书之中,篇次名目均有变动,而“《西镜录》订注”属于失传部分之一.另外梅文鼎在《少广拾遗》中亦谈及此书(详见下文).在焦循(1763-1820)所抄孤本中,有七条梅文鼎订注(“鼎按”)尚能见之.收集当时的数学天文着作,并进行研究订注,是梅文鼎阐述自己数学思想的一种方式.例如在《勿庵历算书目》中,记载梅文鼎订注的书籍就有《天步真原订注》《历学会通订注》.正如《畴人传》的评价:“文鼎每得一书,皆为正其讹阙,指其得失.”[3]但值得关注的是,梅氏七条订注集中在《西镜录》最后的金法、双法和定位法.为便于分析,现将梅文鼎的七条订注胪列如下:
金法第一题: 三人共买房一所,用银二千七百两.乙倍于甲,丙三倍于乙,问各出数.
答: 甲三百两,乙六百两,丙一千八百两.
法: 假如甲出六两,乙出十二两,丙出三十六两,共五十四两,以甲六乘二千七百得一万六千二百,为实,五四而一,得甲出数,倍之即乙丙数.
鼎按: 此在衰分自有本法.甲一衰,乙二衰,丙六衰,并得九衰为法,以除二千七百,得三百为甲数,二乘之得乙六百,六乘之得丙一千八百2.
如梅文鼎所言,此题是衰分的一道基本题型,计算也比较简单.
金法第二题: 五个月用银六十两,今一百三十二两,问用得几个月.
答: 十一个月.
法: 以五月乘一百三十二得六百六十[原作六十六,梅改]为实,以六十而一,得一十个月.
鼎按: 五乘一百三十二是六百六十,非六十六也.虽法、实各降一位,未尝不合,然非所以明算理、开来学也.
此处法实各降一位,指660&pide;60=66&pide;6.这种除数和被除数各自降一位的用法,不是不可以这样做,这种做法终究不是明了算理、启示后人之法.
金法第三题: 买马一匹,园一邱,房一所,用银五千两.园四倍于马,房五倍于园,问各该价.
答: 马二百两,园八百两,房四千两.
法: 假如马三十,园一百二十,房六百,共七百五十,以三十乘五千得一十五万,为实,用七百五十而一,得马价,照法倍之得园、房价.
鼎按: 本法马一,园四,房二十,并得二十五为法,以除五千两,得马二百两.四倍之,得园八,又五倍,得房四千.
此题应用的是衰分方法.
金法第五题: 麦五百担,唤人磨.二人家有五磨,尽一时间甲磨七石,乙磨五石,丙磨四石,丁磨三石,戊磨一石,问几时完及各磨数.
答: 二十五时完.内甲一百七十五石,乙一百二十五石,丙一百石,丁七十五石,戊二十五石.
法:假如四个时,甲磨二十八,乙磨二十,丙磨十六,丁磨十二,戊磨四,共八十.以四时乘五百得二千个时,用八十而一得二十五时,以七石乘之得甲磨数,又以乙五、丙四、丁三、戊一各数乘二十五时,得各磨数.
鼎按: 以八除二百亦得二十五时,然非本数,则乘除之理不明,亦非三率本法也.
“则乘除之理不明,亦非三率本法也”.三率法即今有术,《西镜录》这里是把衰分改为今有术,但还保留着衰分的影子.
金法第六题: 一人为商三次,初次本利约有三倍,二次本利约有五倍,三次本利约有四倍,总之得本利四万,问初、次两商本.
答: 初商本六百六十又三之二,并利二千.次商本二千,并利一万.
法: 假如本银十(丙)[两],以三倍乘得三十,以五倍乘三十得一百五十,以四倍乘一百五十得六百,又以十(丙)[两]乘四万得四十万,以六百而一得六百六十六,不尽,为本银.又以三倍乘之得一千九百九十八.其三之不尽.四以三倍乘得十二,与法六正合,二全数,[并上八作十,进左下,鳞次书圜,以实空位,] [多此数语,欲明反悔]得初商二千,以五倍二十得一万为次商.
鼎按: 原法不谬,但文理不畅,以致惑目,西书出于翻译,多有此等耳.
梅文鼎似觉得此处出于西文翻译,导致文理不通畅,并认为这是从西方着作中翻译所产生的问题.
双法第六题: 两人大小分分银一千两,要大分胜小分四十九两.问各该.
答: 大分五百二十四两二分之一;小分四百七十五两二分之一.
法: 假以大分六百,小分四百,大分多二百,除去四十九,尚多一百五十一.假以大分五百五十,小分四百五十,大分多一百,除去四十九,尚多五十一,与一百五十一相减,存一百为法,以五十一乘六百得三万〇六百,以一百五十(二)[一]乘五百五十得八万三千〇五十,与三万〇六百相减,存五万二千四百五十,以一百而一3,得五百二十四两二分之一,为大分;则小分该四百七十五两二分之一.
鼎按: 一而一与一百而一相去远矣,故定位之法不可不谋也.
梅氏订注指明定位的重要作用.
双法第九题: 天子统师四万征夷,恐不胜,与甲、乙二国借师,甲出师比本国及乙师少一半,乙出师比甲与本国仅得三分之一.问各出师.
答: 甲师三万二千,乙师二万四千.
法: 假以甲师三万,乙与本国倍之应六万,今本国师四万,乙师只二万,以三分之一算,则甲与本国六万,今七万,多一万.假以甲师二万四千,乙与本国倍之,应四万八千.本国师四万,乙师只八千,以三分之一算,则甲与本国应二万四千.今六万四千,多四万,与一万相减,存三万为法.以一万乘二万四千得二亿四千万[依梅改].以三万乘四万得一十二亿[依梅改],相减,存九亿六千万,以三万而一得甲师三万三千,乙与本国倍之,得六万四千,除去本国四万,存二万四千为乙师.
鼎按: 算家定位之法不明,每见因乘骤升,辄骇其数之多,而以意名之,以百名亿,以单六名六万,后之学者,又何以得其根元乎?
此处的订注,梅文鼎针对过去的定位不明确,由于乘法位数上升,数目巨多,这里新命名之法使数目众多的问题得以解决.值得注意的是,此段算法中有两处加注“依梅改”(图1),这表明梅氏对本题进行了认真校算.梅氏在其《笔算》特别强调“定位”的重要性,如其“异乘同除定位诀”中所言:“握算者或疑其数之聚升,而不能守其定法,则定位必讹,而其理益晦矣.故复论之.”其下注曰:“诸家筭术,往往有定位不确者,皆由见乘后数多,未免警怖,而辄为酌改,故也.”这段内容与《西镜录》中的上注极相似,应是因上注的算理来源4.
从上述七条“鼎按”,可以发现梅文鼎似是逐题研读,纠正了若干数字错误,给出自己的解答和评论,这些文字反映了梅文鼎研究此书的学习心得.从注文可见,梅文鼎比较关注《西镜录》中的金法,即“今有术”,双法即“盈不足术”,以及定位法.
2 、梅文鼎的《少广拾遗》《笔算》与《西镜录》的关系
梅文鼎如此详细订注《西镜录》,其笔算着作中是否有受到《西镜录》的影响呢?据梅文鼎年谱的记载,1692年梅文鼎订注《西镜录》,之后写成《少广拾遗》,到1693年2月自序所着《笔算》五卷.从时间上看,这两本书中的内容与《西镜录》若有相似的内容,应可判断二者之间有所联系.接下来将考察这两本书[4].
《少广拾遗》是梅文鼎答复朋友关于开高次方的问题,系统阐述了立成释锁法[5].其序言中有:“尝见《九章比类》《历宗算会》《算法统宗》,俱载有开方作法之图,而仅及五乘,并无算例…….《同文算指》稍变其图,具七乘方算法;《西镜录》演其图为十乘方,而举数仅详平立三乘.”[6]按照潘亦宁的分析,从梅文鼎认为《九章比类》和《历宗算会》“并无算例”,可见梅文鼎只是见过这两本书,并没有仔细研究过.因此《少广拾遗》主要参考的是《同文算指》和《西镜录》[7].
在《少广拾遗》的开篇,就有开方求廉率作法本源图(图2),但是此为开八乘方图,后又有开十二乘方图.梅文鼎见过《西镜录》中的开至十乘方,推测其推广至十二乘方自然是合乎情理的.
图2 《少广拾遗》中的开八乘方图和开十二乘方图
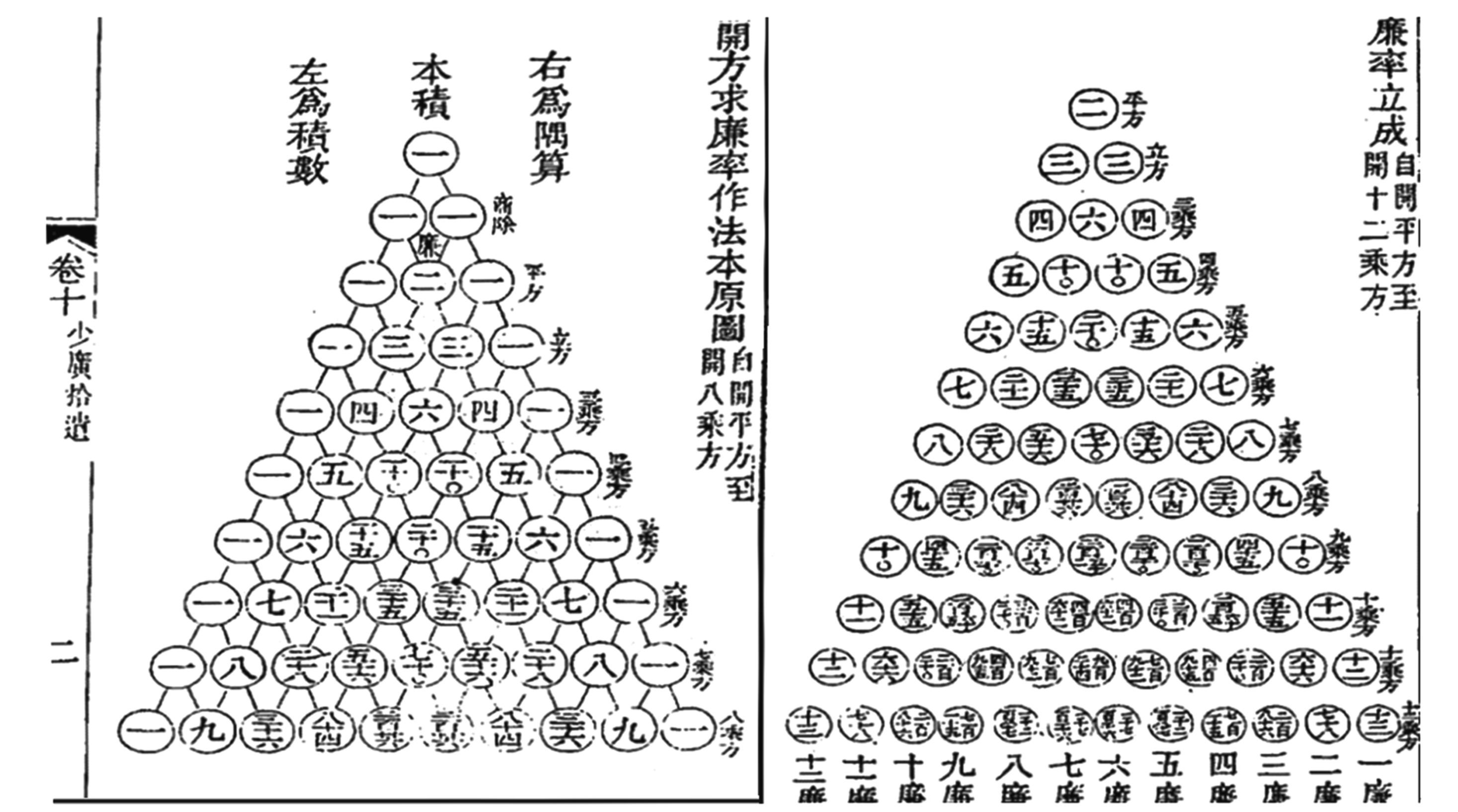
Fig.2 Binominal Coefficient Table for 9th Power and 13th Power in Shaoguang Shiyi
《少广拾遗》中有初商表,它列出了1到9从开平方到开十二乘方的 “各廉率”.在《西镜录》的“见根开三乘方”中有“初商三乘除实立成捷诀”,它给出开三乘方(4次方)的 “各廉率”.可以推测梅文鼎发现先列出初商表,对于之后开方的时候计算带来简便,因而把1到9的十三次方都列表于书中.
关于“做点定之”,即定位问题,梅文鼎自述:
“又按开方分段,古人旧法之精,钱塘吴信民《九章比类》,山阴周述学《历宗算会》悉着其说,而《同文算指》《西镜录》本其意以作点定之,施于笔算为极善也.鼎于三十年前见《同文算指》作点之法,惊叹其奇,后读诸书,始知其祖述,非西人创也.”[8]
这里可以看到梅文鼎对《同文算指》和《西镜录》的以点定位之法的惊叹,以及后来读到古代数学,发现其古已有之.这里梅文鼎把《西镜录》和《同文算指》一样皆看作西法,可见在梅文鼎心里,《西镜录》亦为西方笔算的翻译之书.
《笔算》是梅文鼎按中国人的书写习惯对西方笔算进行中国化改造的一部笔算数学着作.是书分为五卷,分别介绍了四则运算、列位、检验法、约分、通分、开平方、开立方等算法知识.梅文鼎在序言中即言明:
“天方国字,自右而左,欧逻巴字,自左而右,皆衡列为行,彼中文字尽然也.彼之文字既横,故笔算亦横,取其便于彼用耳,非求异于我也.吾之文字既直,故笔算宜直,亦取其便于用耳,非矜胜于彼也,又何惑焉.”[9]
因此在《笔算》中梅文鼎按照中国人习惯的方式对《同文算指》《西镜录》的算式进行了竖排改造.再比如《笔算》第一卷有“透支转减法”“淮仓销算”等实际的问题作为小标题,与实际生活紧密相连,可见梅文鼎“征之于实”的数学思想.
在对乘法定义时,梅文鼎言明:“以数生数,是之谓乘,数不能自生,相得乃生,故乘亦曰因.生则不穷,故乘有升义,生则日积,故乘有载义.有一位乘,有多位乘,或分一位曰因,多位曰乘.”[9]859晚清传教士伟烈亚力所着《数学启蒙》亦引用此说:“乘者,生数也.以数生数,有生生不已之意焉.单数曰因,众多曰乘,通而言之曰乘也.”[10]一位乘法为因,多位乘法为乘,此应来自《同文算指》“既知加减当论因乘,单位曰因,位多曰乘”[11].
但梅文鼎所言“《西镜录》不知谁作,然其书当在《天学初函》之后,知者《同文算指》未有定位之法,而是书则有之.”此定位之法在《同文算指》前编即有“定位第一”,那梅氏为何称“未有定位之法”?下面以乘法中的一题为例探究此问题.
“假如有金九钱八分五厘,每两价银八两八钱,问该若干.答曰:八两六钱六分八厘.先以法八钱乘实数五,呼五八成四十,纪○于本位,纪四于进位.进乘实数八,呼八八六十四,纪四于本位,纪六于进位,乘实数九,呼八九七十二,纪二于本位,纪七于进位.次进一位,以法八两乘实五,呼五八成四十,纪○于本位,纪四于进位.进乘实八,呼八八六十四,纪四本位,纪六进位.进乘实九,呼八九七十二,纪二本位,纪七进位.乘毕,以并法合总.定位法: 原问每两之价,而实无两,当于实九钱上补作○,两位为根,以横对得数定为法尾,钱即上下之位,俱定.定位又法: 此小数也,原问以每两价为法,而实有钱分厘,共小三位,即于得数截去尾三位,定第四位为六钱,法实减余平列左上,相乘而减之,列左下,得数减余列右下,以相同为定.”
从图3与算理可以看出,其做法与《同文算指》《西镜录》等笔算思路一致,只是将横排变成竖排,把法数放在下方,实数放在右方.但定位法是沿袭《西镜录》中的做法,如《西镜录》中类似问题:“金七钱零三厘六毫,每两易银七两六钱五分,问总.”同样是金银兑换,在定位处理上,“定位以实中每两为根,就根位呼法尾为六数向左得两”(图4).而《同文算指》中定位只是区分了大小数、十进制这样的问题[12],且后面的乘除皆是整数乘除,而《西镜录》乘除法皆采用小数的计算,因此可以理解梅文鼎为何称“《同文算指》未有定位之法”.当然还涉及钱的单位,物的量度单位,这样的定位问题,不似《同文算指》中有的只有纯数字计算的问题.
图3 梅文鼎《笔算》中的乘法算例

Fig.3 Multiplication in Mei Wending's Bi suan(Manual calculation)
图4《欧罗巴西镜录》中的乘法算例

Fig.4 Multiplication in The Records of Europe's Western Mirror
图5 梅文鼎《笔算》中的定位法
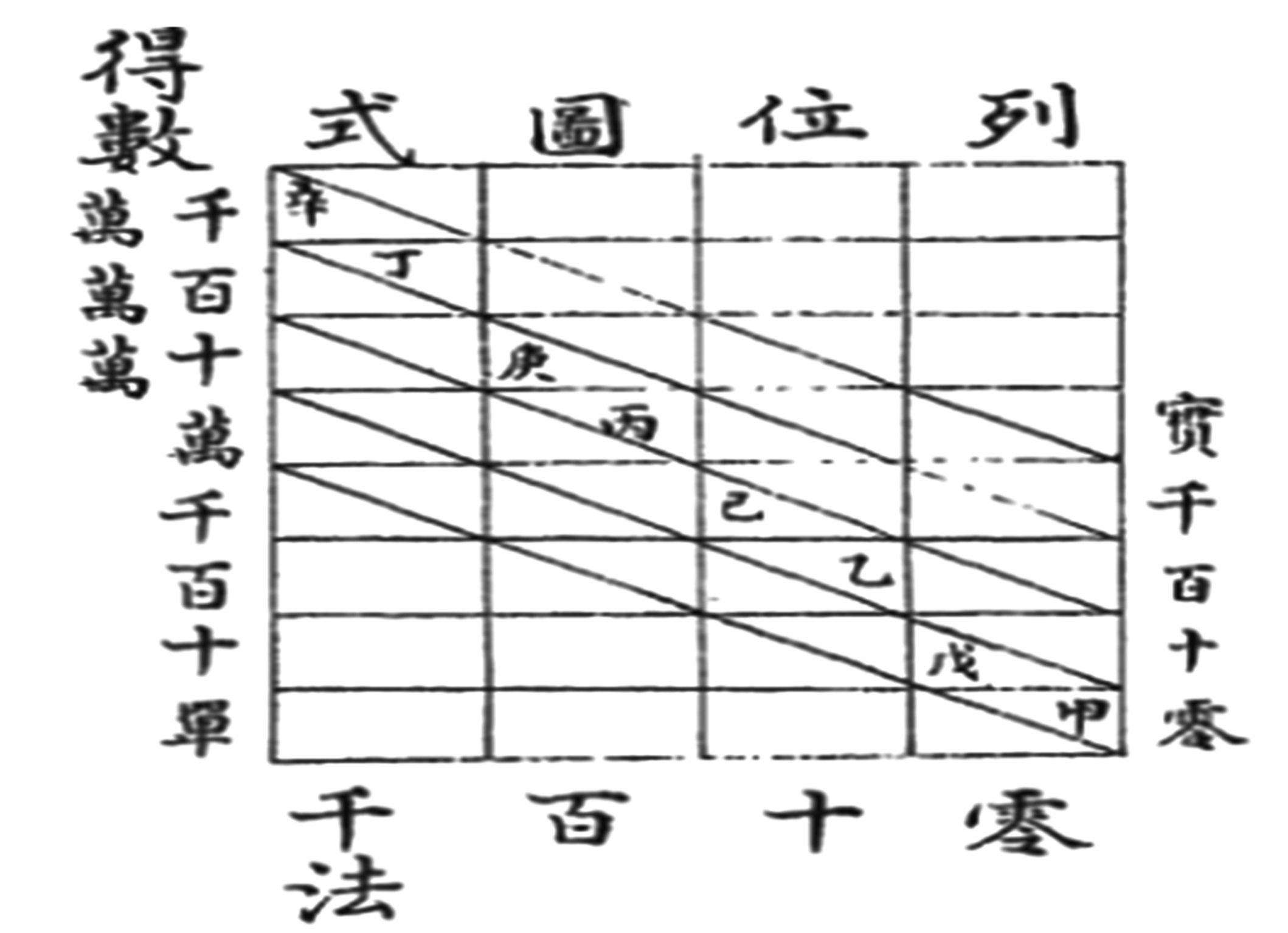
Fig.5 Positioning Method in Mei Wending's Bi suan (Manual calculation)
梅文鼎所用定位又法,应是其自己创新出的列位图式(图5)的应用.
“凡实数纵列于右,凡法数横列于下,纵横相遇而得数生焉.直行所对者法数也,斜行所对者实数也,而纪得数则以横行定之.或问实何以对斜行?曰: 法有进位,故得数斜升,是故右第一行是法单位乘出之数也.其次行,则法十位乘出之数也.又次而百、而千,视此矣.故其乘得数不出斜格,此虚位也,单、十、百、千,周流迭居,皆于临时定之.”[9]867
此段解说应是从格子乘法中脱胎而出.《九章算法比类大全》称之为“铺地锦”(图6).
其他如省乘法、省乘又法、截乘法等皆是珠算中曾有的对某些特殊数字的更简便的乘法计算方式.
在除法的讨论上,“以数剖数,是之谓除.除其原数,以归各数,故除亦曰归.除与乘对,理精用博.近或谓之分,义则浅矣”[9]863.梅文鼎这里对除法的定义与《算法统宗》中“除者以数剖数也,除其原数,以归各数,故曰归”相类似.但对于“分”这样的定义,梅文鼎认为意义有些浅显了.分在《西镜录》和《太西算要》中皆出现过,对此问题的判断,亦可说明作者必仔细研读思考过.“假如有额编地丁银二百一十一两一钱四分,其科则每亩六分.问原地若干”[9]866.《算学发蒙》有相同的题.其他如命分法、省除法、省乘又法、截除法、约分法等都是一些简便的除法计算方式.
图6 吴敬《九章算法比类大全》中的格子算法

Fig.6 The Chessboard Multiplication in Wu Jing's Great classifiedsurvey of the Nine chapters on mathematical methods
在试法部分,梅文鼎提出简法.
“论曰:除法以乘法还原,犹之乘法以除法还原,此旧法珠算所必需.若除法以除法还原,则旧所无也.《同文算指》用九减七减试法可免还原,颇称巧捷.今以并法代之,则试法亦省.故称简法焉.兹各具一则,用相参互,以明筭理,握算者择而用之可也.今定笔除只用简法还原,若笔乘仍用试法.”[9]814
此处其言“并法代之”,应是后面在并除法中所用,例如除以7,除以8并为除以56.
在第三卷关于西人三率法问题,梅文鼎敏锐地观察到了它们和《九章算术》之间的联系:
“以先有之数知今有之数,两两相得,是生比例,莫善于异乘同除,乃古九章之枢要也.先有者二,今有者一,是已知者三,而未知者一,用三求一,故西法谓之三率.”[9]874
《同文算指通编》开篇便是“三率准测法第一”,梅文鼎在《笔算》“变测法”中亦提到《同文算指》:
“凡异乘同除:皆以先有之一率为法,即首率.以先有之又一率乘今有之一率为实,即二率、三率相乘.若同乘异除,则反以今有之一率为法,《同文算指》列于第三,今依法实之序定为首率.以先有之两率自相乘为实,《同文算指》列于第一、第二,今定为第二、第三.虽亦以法除实,得今所求之又一率,即四率.与诸三率同,而法实相反,故曰变测.”[9]865
梅文鼎此卷中亦有不少题目来自《同文算指》,如“变测法”的夏布四十五匹等,此处不再赘述.梅文鼎加以中国化的改造在于“辨法实”:
“然何以定其孰为一率,孰为二率、三率也?曰:此则古人同异名之法,不可易也.”
以哪个作第一率,哪个作第二率、第三率,这件事不能含糊其辞,应按照古人的做法.这与刘徽“今有术”注释所称“因物成率,审辩名分”[13],若合符契.对于开平方、开立方问题,梅文鼎不仅用求初商,次商等一步步求得,也试图采用传统数学中廉隅法构建正方形、正方体来“以图明之”.
3、 结语
本文通过对《西镜录》中梅文鼎的注文来探究西算对梅氏着作的影响,以期窥测清代学者对西方笔算数学的吸收.从梅文鼎对《西镜录》的订注可以看到梅氏点评中所蕴含的思想:
第一,梅文鼎重视算法背后的算理(如“虽法、实各降一位,未尝不合,然非所以明算理、开来学也”“然非本数,则乘除之理不明,亦非三率本法也”).第二,梅氏发现西学翻译中的问题(“原法不谬,但文理不畅,以致惑目,西书出于翻译多有此等耳”).第三,通过对梅文鼎的两本着作《少广拾遗》和《笔算》的分析,梅文鼎对《西镜录》采取了批判和吸收的态度.在对除法本义上,认为采用“分”表示除法,意义尚浅(《西镜录》中采用“分”表示现在意义上的除).而在开乘方表的扩展、初商表的扩展、乘除法中定位法等问题上,能够看到梅文鼎对于《西镜录》的借鉴.由此可见梅文鼎对待西学的态度.
此外,有关《西镜录》与《同文算指》的关系,也可以在梅氏的记录中得知一二.依梅文鼎《勿庵历算书目》所言,“《西镜录》不知谁作,然其书当在《天学初函》之后.知者,《同文算指》未有定位之法,而是书则有之,其为踵事加精,可见所立金法、双法,亦即借衰互征、叠借互征之用,然较《同文算指》尤觉简明.但写本殊多鲁鱼,因稍为之订”[14].据此说可知,其一,在1692年梅文鼎所熟悉的历算同仁圈子内都“不知谁作”,显然《西镜录》在写成后未刊印,也未署名,或者署名页丢失,只在私人之间流传,梅文鼎为其作了订注.其二,从对金法、双法和借衰互征、叠借互征之比较,梅文鼎注意到《西镜录》 “然较《同文算指》由觉简明”.其三,《同文算指》未载定位之法,而《西镜录》有之,而且“踵事加精”,故梅文鼎认为《西镜录》当在《天学初函》(1629年刊刻)之后,而非在《同文算指》(1613年刊刻)之后.《天学初函》分为“理编”和“器编”,《同文算指》被收入其“器编”中,加之“《天学初函》在明季流传极广,翻版者数本”[15].因此梅文鼎所读《同文算指》有可能属于《天学初函》本.
综上所述,《西镜录》作为西方笔算数学的传入之一,虽不似《同文算指》翻译完整的数学文本,但它是中国学者在传统数学的基础上吸收西方笔算方法的一部会通中西之作.
参考文献
[1] 欧罗巴西镜录 [M]// 郭书春.中国科学技术典籍通汇·数学卷:第4册.郑州:河南教育出版社,1993:279-302.
[2] 钱大昕,窦水勇,校点.竹汀先生日记钞 [M].沈阳:辽宁教育出版社,1998:105-106.
[3] 阮元.畴人传合编校注 [M].郑州:中州古籍出版社,2012:330.
[4] 李迪.梅文鼎评传 [M].南京:南京大学出版社,2006:432-433.
[5] 刘钝.少广拾遗提要 [M]// 郭书春.中国科学技术典籍通汇·数学卷:第4册.郑州:河南教育出版社,1993:409.
[6] 梅文鼎.少广拾遗 [M]// 郭书春.中国科学技术典籍通汇·数学卷:第4册.郑州:河南教育出版社,1993.
[7] 潘亦宁.梅文鼎对方程解法问题的研究 [J].西北大学学报(自然科学版),2012,42(4):698-702.
[8] 梅文鼎.少广拾遗 [M]// 郭书春.中国科学技术典籍通汇·数学卷:第4册.郑州:河南教育出版社,1993:718.
[9] 梅文鼎.历算全书 [M]// 《影印文渊阁四库全书》子部天文算法类:第794册.上海:上海古籍出版社,1987:843.
[10] 汪晓勤.中西科学交流的功臣:伟烈亚力 [M].北京:科学出版社,2000:39.
[11] 纪志刚,校点.《同文算指》 [M]// 周振鹤.明清之际西方传教士汉籍丛刊.南京:凤凰出版社,2013:28.
[12] 陈敏皓.《同文算指》之内容分析 [D].台北:台湾师范大学数学系,2002.
[13] 刘徽.九章算术注 [M]// 钱宝琮,校点.算经十书.北京:中华书局,1963:114.
[14] 梅文鼎.勿庵历算书目 [M]// 王云五.丛书集成初编:第20册.上海:商务印书馆,1939:33.
[15] 刘乃和.陈垣年谱 [M].北京:北京师范大学出版社,2002:29-30.
注释
1 何元锡(1766-1829),清代藏书家,金石学家.字梦华,又字敬祉,号蜨隐.钱塘(今浙江杭州)人.钱大昕(1728-1804)弟子.严敦杰《西镜录冥求》中误为“何梦锡”.
2(1)以下所录原文均见《欧罗巴西镜录》,载郭书春主编《中国科学技术典籍通汇·数学卷》第4册,河南教育出版社.1993,281-302
3(2)原文在“一百而一”的“百”字边上打一“△”,可能这个“百”字是梅氏所加,所以才有下面的“鼎按”.—感谢郭世荣教授的意见.
4(3)感谢郭世荣教授提示注意“依梅改”,并给出梅氏《笔算》中的类似注文.





