摘 要: 数学发展史上发生过三次重大危机,对数学的发展产生了巨大影响。就三次数学危机的产生以及危机的解决方面进行梳理,从数学史的视角给出了三次数学危机的启示。
关键词: 数学危机; 数学史; 危机解决;
Abstract: There have been three major crises in the history of mathematics development, which have a great impact on the development of mathematics. In this paper, the emergence and solution of the three mathematical crises are combed, and the Enlightenment of the three mathematical crises is given from the perspective of the history of mathematics.
Keyword: mathematical crisis; history of mathematics; crisis resolution;
0 、引言
经历几千年的发展之后,数学已发展成为一个庞大的学科体系。1868年还只有38个分支的数学学科,到了1979年就发展成拥有约3 400个分支的学科体系。在漫长的发展过程中,数学的发展道路并不平坦,出现了多次危机,而这些危机的解决,进一步促进了数学的发展。本文将就其中的三次重大危机进行梳理,探索这三次数学危机产生的历史根源、思想背景以及危机的解决过程,这对了解数学这门学科的发展脉络、领略数学的旖旎风光与思想方法无疑具有十分重要的意义。

2 、第一次数学危机
2.1、 第一次数学危机的产生
毕达哥拉斯是公元前5世纪古希腊哲学家、数学家、天文学家。相传毕达哥拉斯青年时代曾就学于泰勒斯,后到过亚洲和埃及旅行,特别是在埃及,学到了很多数学知识。约公元前530年,他返回故里,创立了自己的学派—毕达哥拉斯学派。
该学派是一个神秘的宗教组织,主要从事哲学和数学的研究,内部纪律严明,把一切发现归功于学派领袖,而且秘而不宣,以致后人无法得知这个学派的发现是何人在何时发现的。毕达哥拉斯及其学派的思想以及学说是在很久以后,该组织渐渐分散、保密的教条被放弃以后在一些公开讲述该学派教义的着作中逐渐出现的,所以我们今天看到的这个学派的传闻有着不同的版本。
毕达哥拉斯学派在数学上有很大的贡献,论证数学的成长、数学抽象的提出等都归功于该学派。特别是毕达哥拉斯定理,尽管各个文明圈都独立地发现甚至证明了该定理,但西方将之命名为毕达哥拉斯定理,可见世界对该学派数学贡献的认同。
这个学派信奉“万物皆为数”的理念,具体地有两个方面的内涵:(1)宇宙间的一切现象都能归结为整数或整数之比。(2)任意两条线段都是“可公度的”。这里两条线段a、b可公度是指总可以找到第三条线段t,使得a、b的长度都是t的长度的整数倍。
作为学派信条的“万物皆数”在当时一直能解释各种现象,但学派成员根据毕达哥拉斯定理,通过逻辑推理发现,边长为1的正方形的对角线长度既不是整数,也不是整数的比所能表示的,正方形的一边与该正方形的对角线是不可公度线段。
这一发现从根本上冲击了毕达哥拉斯学派的根基,对古希腊的数学观产生了巨大的冲击,引发了第一次数学危机。据传一开始只有毕达哥拉斯学派的成员知道这一结果,内部非常恐慌,极力掩盖事实,希望在内部化解危机。据说学派成员希伯索斯因泄露了这个秘密而被秘密处死(也有传闻说希伯索斯本人就是不可公度比的发现者)。
2.2 、第一次数学危机的解决
古希腊人解决这个问题的基本思路是:在数的领域仍然只承认证书(或整数比),只要在几何的研究中能解决几何量中出现的不可通约(不可公度)量问题就可以万事大吉了。也就是说,把数和量分开处理。
帮助古希腊人摆脱困境的关键一步是由才华横溢的欧多克索斯迈出的。欧多克索斯(公元前408—公元前355)是古希腊着名的数学家、天文学家与地理学家,被认为是古代世界最卓越的创新人物之一。约公元前370年,欧多克索斯天才地给出了“两个量的比相等”的新定义,这是欧多克索斯比例论的核心。他的着作已经全部失传,但幸运的是,他的比例论成果保存在欧几里得《几何原本》的第五卷中,从中可以看到其主要思想。欧多克索斯从这个新定义出发,推出了等25个有关比例的命题。在论证了比例的这些“通常”性质后,古希腊人就能够对几何量之比进行运算了,这与现在我们对实数进行算术运算的方式几乎相同。这样古希腊人部分地消除了危机。之所以说“部分地”消除了危机,是因为“一切都可以归结为整数比”这一命题的错误仍然没有办法消除,彻底解决这一危机是在19世纪,实数理论建立以后的事情。
3 、第二次数学危机
3.1 、第二次数学危机的产生
第二次数学危机则是由牛顿学派的外部、贝克莱大主教提出的,是对牛顿“无穷小量”说法的质疑引起的。16~17世纪,数学家对瞬时速度、切线、极值以及曲线所围图形面积等四大类问题的追究,经过许多数学家的多年努力,终于在17世纪晚期,形成了无穷小演算—微积分这门学科,其中贡献最大的是牛顿、莱布尼兹两位数学家。
但牛顿、莱布尼兹创立的微积分理论是不严格的,两人的理论都建立在无穷小分析上,但他们对作为基本概念的无穷小量的理解与运用比较混乱,推理过程中存在着明显的矛盾。以求自由落体的瞬时速度为例:
设自由落体在时间下落的距离为,有,其中是固定的重力加速度。我们要求物体在的瞬时速度,先求,我们有:
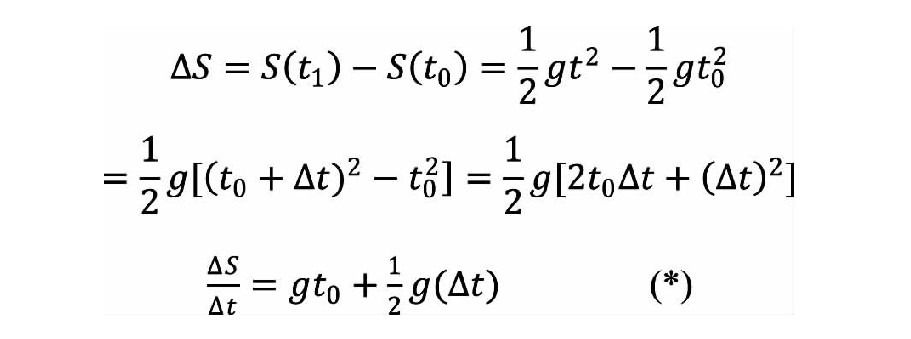

前面提到的其他三类主要问题也采用这样的无穷小分析方法,都得到了解决,这一方法也成功地用在解决过去大量的科技问题上,因而得到了广泛的认同,并得以迅速发展。
但是当时的微积分理论虽然在计算上能方便地解决许多的计算问题,可对作为基本概念的无穷小量的理解与运用却是混乱的,模糊不清的。围绕“无穷小”作为一个量,究竟是不是0?微积分理论的创立者在推导过程中对“无穷小”的属性的说明是不一致的。
对微积分理论发表文章进行猛烈攻击的是英国的贝克莱大主教。贝克莱指出,对于(*)式而言,当为0,左边没意义,若不为0,则右边的第二项不能任意去掉。从形式逻辑而言,这无疑是一个矛盾。贝克莱提出的这一问题数学史上称之为“贝克莱悖论”,在当时的数学界引起了一定的混乱,导致了第二次数学危机的产生。牛顿与莱布尼兹都曾试图完善微积分理论,解决这一引发数学界混乱的问题,但都没有获得成功。
3.2 、第二次数学危机的解决
为了补救第二次数学危机,数学家们开始严格化重建微积分。微积分的创立者牛顿、莱布尼兹自身也做了很多努力,但问题没有得到解决。此外,英国数学家泰勒在微积分创立之初也曾努力地去弥补被遗留的难题,但是尝试没有取得成功。
在贝克莱悖论提出后的7年,出现了30多种的小册子和论文试图消除悖论并回击贝克莱的批评,并把主要的努力投入到微积分基础的严密化尝试中。其中,英国数学家麦克劳林对贝克莱悖论做出了最重要的回应,他采取了拒斥无穷和无穷小量概念,用几何方法严格论证微积分的做法。
但这样的工作没有获得18世纪大多数数学家的认同,因为麦克劳林的方法退回到了古希腊人的烦琐方法,这样做就放弃了微积分理论的优点:迅速而有效地解决重要的计算问题。因此数学家需要寻找其他途径加固微积分基础。
18世纪更多消除贝克莱悖论的工作是由欧洲大陆数学家完成的。欧拉、达朗贝尔、拉格朗日、卡诺等做出了较大的贡献。其中达朗贝尔设法利用极限的方法给出微积分的理论依据,拉格朗日设法放弃无穷小量的概念,卡诺则采取了用事实证明和说明无穷小的现有算法。但整个18世纪,人们都试图为微积分找到合乎逻辑的理论基础,几乎每一个数学家也都做出了一些努力,虽然有一些发现,但所有的努力都没有获得圆满的结果。
微积分理论的严格化最终由19世纪的数学家来完成。挪威数学家阿贝尔,捷克数学家波尔查诺、法国数学家柯西、德国数学家魏尔斯特拉斯、戴德金、意大利数学家皮亚诺等做出了主要的贡献。其中贡献最大者首推法国数学家柯西,他写出了一系列着作,他在《分析教程》和《无穷小计算讲义》中给出了数学分析一系列基本概念的精确定义,例如:他给出了精确的极限定义,然后用极限定义连续性、导数、微分、定积分和无穷级数的收敛性。而魏尔斯特拉斯则创造性地使用语言,为数学分析奠定了严格的基础,使之达到今天所具有的严密形式。最后由戴德金、魏尔斯特拉斯、皮亚诺等数学家完成了严密的实数、有理数、整数理论体系的构建。至此,人们认为,数学基础的第二次危机已经克服,数学的整个结构已被恢复,数学建立在无懈可击的基础上了。
4 、第三次数学危机
4.1、 第三次数学危机的产生
19世纪末和20世纪初,数学迎来了空前兴旺发达的时期。首先是数理逻辑学科的诞生,实现了逻辑的数学化。19世纪70年代,德国数学家康托尔创立了集合论,旨在为数学学科奠定坚实的基础。19世纪末戴德金和皮亚诺对算术及实数理论进行公理化,希尔伯特则完成了初等几何的公理化。同一时期,现代数学的一些新兴分支,如抽象代数学、点集拓扑学、代数拓扑学、泛函分析、测度与积分理论等也得到蓬勃发展。
数学学科取得的一系列巨大成就,令数学家振奋。1900年,在巴黎召开的国际数学家会议上,法国大数学家庞加莱兴奋地宣布:“我们可以说,现在数学已经达到了绝对的严格”。但数学家们很快发现了集合论内部存在的问题,他们提出的多个数学悖论让数学大厦又一次受到强烈冲击,引发了第三次数学危机。这些悖论中包含了康托尔本人发现的悖论,但康托尔等人提出的悖论并未引起数学家的重视。一直到1902年罗素悖论的出现,终于引起了数学界的极大震动,围绕集合论形成了20世纪初数学基础的大论战。
罗素悖论可以这样描述:以M表示“是其本身成员的所有集合的集合”,以N表示“不是它本身成员的所有集合的集合”,问,集合N是否是它本身的成员?
我们可以通过推理得出:无论是哪种情况,都出现矛盾。
罗素悖论曾被以多种形式通俗化,其中最着名的是罗素于1919年给出的“理发师悖论”:某村有个理发师,宣布了这样一条原则:他给且只给村里不自己刮脸的人刮脸。问:理发师是否给自己刮脸?如果他给自己刮脸,他就属于自己给自己刮脸的人,按规则,理发师不应该给他自己刮脸,矛盾。如果他不给自己刮脸,他就属于自己不给自己刮脸的人,按规则,理发师应该给他自己刮脸,这又矛盾。无论是哪种情况,都出现矛盾。
罗素悖论比起之前的数学家提出的悖论以简单明了的方式揭开了集合论本身矛盾重重的盖子,震惊了整个数学界。法国数学家、数理逻辑先驱弗雷格当时正准备出版《算术的基本法则》第二卷,收到罗素的信后,只能把自己为难的心情写在新着的末尾:“对一位科学家而言,最难过的事情莫过于在他的工作即将结束时,其基础崩溃了。”提出算术公理完整系统的德国数学家戴德金也因此推迟了他的《什么是数的本质和作用》一文的再版。
4.2 、第三次数学危机的解决
危机产生后,数学家纷纷提出自己的解决方案。数学家开始了对康托尔集合论的改造,主要是通过对集合定义加以限制来排除悖论,这就需要建立新的原则。这些原则既要保证能排除一切矛盾,又能使康托尔集合论中一切有价值的内容得以保存下来。1908年,策梅罗在自己这一原则基础上提出第一个公理化集合论体系,后来经弗伦克尔的改进,形成了着名的Zerme-to-Fraenkel(ZF)集合论公理体系,之后在ZF公理体系的基础上添加了选择公理,形成ZFC集合论公理体系。这一公理化集合系统很大程度上弥补了康托尔朴素集合论的缺陷。除ZFC系统外,集合论的公理系统还有多种,如冯·诺伊曼、博内斯、哥德尔等提出的NBG系统等。公理化集合系统的建立,成功地排除了集合论中出现的悖论,从而比较圆满地解决了第三次数学危机。
尽管悖论可以消除,矛盾可以解决,然而数学的确定性却在一步一步地丧失。现代公理集合论中一大堆公理,简直难说孰真孰假,可是又不能把它们都消除掉,它们跟整个数学是血肉相连的。所以,第三次数学危机表面上解决了,实质上以其他形式更深刻地延续着。
在另一方面,罗素悖论对数学而言有着更为深刻的影响。它使得数学基础问题第一次以最迫切的需要的姿态摆到数学家面前,导致了数学家对数学基础的研究。而这方面的进一步发展又极其深刻地影响了整个数学。如围绕着数学基础之争,以罗素为代表的逻辑主义、以布劳威为代表的直觉主义、以希尔伯特为代表的形式主义三大数学哲学学派(数学基础的三大学派)应运而生,而各派之争又促进了数学的大发展等等。
5 、三次危机对我们的启示
三次数学危机能给人很多启示,本文从数学史的角度去思考,能得到以下启示:
(1)首先是理解无限并非易事。无理数的发现导致了第一次数学危机,而无理数实际上就是无限不循环小数;第二次危机,正像贝克莱指责的那样在“无穷小量”上,实际上要害的核心极限理论的逻辑基础不完善;而第三次危机,涉及无穷集合,也与无限有关。可以看到,三次危机都与无限有关。现代人在学习、理解涉及无限的概念或现象、解决涉及无限的问题是也常常发生困难,由于人们习惯于有穷情况下的思维,往往从有穷状况类比、推断无穷情况、认知未知情形、未知世界,而有穷与无穷有着本质的区别,因此一旦遇到无穷时要格外谨慎。
(2)数学发展的历史有助于深入理解数学。数学学习中我们经常遇到会有许多如下的疑惑:为什么古希腊数学家喜欢用几何方法研究处理数学问题?为什么把无限不循环小数叫做无理数?数学的理论或结构是如何建构的?为什么要进行证明?为什么有的教科书对平行线给出“同一平面内垂直与同一直线的两条直线”这样的定义,而不用“同一平面内永不相交的直线呢”?为什么要这样构建公理系统?戴德金分割和皮亚诺公理有什么意义?这些问题在教科书中找不到现成的答案,绝大部分教师也不会提及会解释这些问题。而通过前面的讨论我们对这些问题会在某种程度上找到答案。比如对教科书中平行线的两种定义,实际上是数学哲学三大流派中直觉主义与形式主义的“代表”,是否“永不相交”无法判别,形式主义给予认可,但直觉主义则希望能实实在在地进行判断,而采用垂直于同一条直线这样的说法。
6 、结语
通过对三次数学危机发生、发展史的考察,我们对数学的理解能得到提高。相对数学世界的瀚海大海,限于目前已知的狭隘知识面,我们对数学的认知目前还是冰山一角。如果我们能比较全面、系统地了解数学的发展史,无疑能提高我们对数学理解的高度以及深度。
参考文献
[1]韩雪涛.数学悖论与三次数学危机[M].北京:人民邮电出版社,2016.
[2]兰林世.三次数学危机与悖论[J].集宁师专学报,2003(4):47-49.
[3]李改杨.数学文化欣赏[M].北京:科学出版社,2011.
[4]宋述刚,谢作喜.试论数学危机与数学的发展[J].长江大学学报(社会科学版),2010(5):51-53.
[5]王保红.数学三次危机的认识论意义[J].山西教育学院学报,2001(4):106-107.
[6]王炳福.回顾与思考---试论三次数学危机及其启示[J].山东大学文科论文集刊,1984(2):167-180.
[7]王庚.数学文化与数学教育---数学文化报告集[M].北京:科学出版社,2004.
[8] 薛有才.数学文化[M].北京:机械工业出版社,2013.
[9]易南轩,王芝平.多元视角下的数学文化[M].北京:科学出版社,2007.





