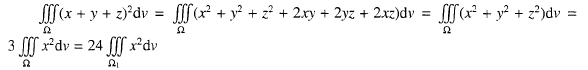本篇论文目录导航:
【题目】
中学数学教育中数学美的价值探究
【第一章】
我国中学数学教育美学问题研究绪论
【2.1】美学与数学美
【2.2】
数学美在中学数学教育中的作用
【2.3】
数学美对学生素质的影响
【2.4】
深化数学美的探究,全面推进素质教育
【3.1 】
中学数学教育中的审美教育
【3.2】
审美教育的意义
【3.3】
数学美在中学数学教学中的渗透
【3.4】
数学美融入中学数学教学中
【3.5】
教师是影响学生对中学数学美感受的关键因素
【3.6】
感受美,欣赏美的渠道
【参考文献】
数学美与中学数学教育的结合研究参考文献
第二章数学美在中学数学教育中的作用。
2.1美学与数学美。
2.1.1美学的概念。
1美是人类创造性实践活动的产物。所谓的数学美,是指利用审美的观念对数学的一种哲学研究。四〕美存在于文学,艺术中,社会生活中,我们称之为艺术美还有一种存在自然科学中的理论美,其内涵包括逻辑美,结构美和公式美,我们称之为科学美。数学美隶属于科学美,具有一般语言文学和艺术所共有的美的特点。数学在其内容结构上和方法上也具有自身的某种美,也称之为数学美。数学不但具有严密的逻辑性和一定的抽象性,同时也拥有至高无尚的美,美是数学的灵魂。数学美是自然美的客观反映,是科学美的核心。
数学中美的因素处处可见,无论数学中的公式,还是含义无不体现着数学的美。无论把数学比作诗歌,还是乐章,都是在说数学的美。所谓数学美的含义是丰富多彩的,如数学体系的完善,数学结构系统的协调,普遍性,数学概念的简洁而精确,数学定理的概括,数学公式的简洁,完整,数学思维的独特性和奇异性,数学图形的和谐性,对称性,数学方法的奇妙性等,都是数学美的表现形式。
2.1.2数学美学的产生与发展。
美学是一门古老的科学,社会的进步就是人类对美的追求的结晶。人类对于数学美的追求以及关于数学美的观念等,随着人类早期数学的出现就出现了。同样人类对数学美学的研究,也早在古代的时候就开始了。数学美的产生与发展的,经历了以下三个时期:
1.数学美的朦胧时期。
数学是一门抽象化,以逻辑推理为主的,有组织的、独立的学科,在很早的时远古时代,数学就己有了开端和萌芽。我们称之为早期数学。在那时,数学就已经伴随着一种朦胧而神秘之美了[11].早期时候,人们识数能力有一定的限制,差不多是不超过头十个的数,被认为是被神秘的气氛包围着,因而都具有神秘的色彩。
翻开古代四大文明古国的历史,就可以看到在这些文明古国的早期数学中,呈现出来一种朦胧而又神秘的美。在我国古代,太极八卦中,就已展示出数学的美。圆有无数条对称轴,是一切平面图形中最美的图形。而太极图的发明被认为那时的人对圆所呈现的美就已经有了初步的认识。相传由伏羲,文王所作的《周易》一书中,就己经有了阴阳奇偶的说法,即把奇数定为阳,那么偶数则为阴。同时在我国的童话中,又把奇数象征白、昼、夜、热、日、火、天偶数象征黑、夜、冷、物、水、地。
巴比伦人在公元前2000到1600年就已经感受到几何图形的美,巴比伦人已掌握直角三角形、长方形和等腰三角形等简单平面图形的面积,还有一些简单立体图形如长方体及特殊梯形为底的直棱柱等图形的体积的方法。巴比伦人对圆的图形上显示出来的对称美,和谐美感受更深,表现为他们知道直径的三倍为圆周,把圆周分成等分,圆周平方的1/12为圆的面积等等。
埃及人的数学并不比巴比伦数学高明,总的来说,他们的数学是简单而粗浅的。被称为“最伟大的埃及金字塔”的莫斯科纸草书的第个问题中的数值例题是埃及凡何学中最了不起的例子,因为它用具体数学写出的表达式呈现出对称美。无论埃及还是巴比伦,他们都认为数学本身有神秘的特征,并可以预卜未来,对自然界和人类社会中的现象作神秘解释。印度的数学和宗教、占星术有密切联系,带有深厚的宗教气味,公元前6世纪创造出一些原始数字。
综上所述,可以看出数学在早期时代就呈现了朦胧美,想要进一步发掘早期数学中的美,还需要我们进一步的研究。
2.数学美的萌芽时期。
古典数学时期,人们开始关注数学与美学的关系,是数学美的萌芽时期,这个时期的数学是属于常量、初等的数学范畴。在这个时期,人们开始注意到了数学与美学之间的关系,并对这种关系进行了有意识地探索与论述,促使了数学与美学关系的发展。之所以称它是数学美的萌芽时期,有二个原因第一,这一时期的数学美学思想仍明显的带有朦胧时期那种神秘主义的色彩。在古代,美学思想通常都以哲学论述的形式出现,而古代的科学和艺术是统属于哲学之中的,因而,很难把数学中的美学思想与哲学思想截然分开。人类进入文明时代之后,一直试图寻找各种自然现象的统一本原。对此,各古代民族几乎一致认为,世界存在着一个统一的本原。无论是东方还是西方,在古典数学的时期中,数学的美学因素,有形无形中仍与神学纠合在一起,蒙上了一层神秘的色彩。这正反映出数学美刚破土萌芽,显得幼弱而娇嫩,只有借助于神学的力量才能生存。
第二,这一时期的数学美的表现形式还是低层次的,外层次的,主要是表现数学理论,图形之中关系的定理和公式所呈现出来的形态美。古希腊的毕达哥拉斯学派的美学理论是西方古代美学的开端,认为美与事物形式所表现出来的均衡,对称,比例,和谐,多样统一分不开。认为美完全可以用严格的数来加以表达,数学的本原就是万物的本原。这大概是数学与美学之间的关系的最早的论述。毕达哥拉斯有句名言,凡是美的东西都具有一个共同的特征,这就是部分与部分之间,以及整体之间固有的协调一致。毕达哥拉斯学派把均衡与对称作为按照数学的秩序所构成的形式之一,视之为一种美。均衡是事物各部分、诸元素在数量关系上大致相等,分布匀称,有着一种合理的数量关系,因而能生成和谐之美。
在古典数学时期,无论是东方还是西方所表现出来的数学美主要是数学语言美以及以均衡、匀称、对称、比例、和谐等为特征的数学形态美。但仅仅都是外层次的、低层次的,很少涉及到数学的内在层次美。
3.数学美的发展时期。
数学的发展有赖于社会环境,17世纪的政治、经济和社会的发展,给予了数学巨大的推动。我们称世变量数学、高等数学的这一时期的数学为现代数学川。数学美的思想不在以毕达哥拉斯的以猜想为主,已经超越了那一阶段,进入到数学的理论体系的阶段。在那个时期,经典数学达到了数学形态美的发展高峰,继续向数学在内在结构美,数学逻辑美方向发展。
20世纪50年代以来,随着科学在分化与综合这两方面的迅速发展,一些传统美学思想开始有所突破。控制论、信息论、系统论的出现,为数学美学的发展开辟了新的广阔领域。模糊数学和突变数学的兴起,为数学美找到了新的起点。譬如数学中既有渐变之美,也存在突变之美,既有精确性的美,也有不精确的美。此外,科学语言与艺术语言的有机结合,抽象美感与美感直觉的相辅相成,逻辑思维与形象思维的相互补充,以及数学中真、善、美的统一问题,必将成为我们研究数学美学的新课。这些问题的解决,将会极大的丰富数学创造和数学美学的内容。
2.1.3数学美的分类及特征。
数学发展的历史处处闪耀着数学美。事实上,数学研究与数学美的联系源远流长,对数学美的探索已历时数千年[14].数学美是社会属性与物质属性的有机统一,其社会性构成了数学美内容方面的因素。其物质化构成了数学美形式方面的因素。因此,我们可以从内容与形式两方面对数学美进行分类,并分析其基本特征。
1.数学美的分类。
随着历史和科技的发展,数学美也随之变化和发展。但数学美的内容和基本特征却有它们的相对稳定性。数学美的内容和特征,就是数学家们所重视的理论和方法的优美。根据理论与方法这两个方面,我们将数学美分为结构美,语言美和方法美。数学结构美是一种内在的美,特别是在数学解题中存在很多结构美,通常表现为数学元素的完备整齐,式子结构的对称有序。数学结构美来自于各部分的和谐秩序。正是这种内在美给了满足我们感官的一个美丽的骨架,使我们面对一个秩序井然的整体,能够预见数学定理。
数学语言作为一种表达科学思想的通用语言和数学思维的最佳载体,它有一整套数学符号系统。数学符号系统有三个很大的优点确切性、经济性和通用性。数学相比起其他的学科来说,具有更完美的语言形式,它能够突破各民族语言的隔阂而成为全人类共同的统一的表述工具。对于全世界各民族的人来说,只要具备了一定的数学素养,对于同样的一个数学符号公式,大家都可以确切的理解它的复杂涵义。因此,可以说数学语言,以它的简洁、概括、富于形象化、理想化的特征和形式,给人们以美的感受。简洁和谐、有序就是数学语言美的基本特征。
2.数学美的特征。
数学是研究数量关系和空间形式的科学。数学特有的抽象概念,公式符号,推理论证都体现了数学美。数学方法的简洁性,典型性,和奇异性能给人们美的感受。无论从数学美的内容,还是从数学美的形式方面来讲,数学美的特征都表现为简洁性,统一性,对称性,整齐性,奇异性与思辨性这几方面。
(1)数学美的简洁性。
简洁性是数学形态美的基本内容。爱因斯坦说过“美,本质上终究是简单性。”他认为,只有借助数学,才能达到简单性的美学准则。[15]最简洁的数学理论最能给人以美的享受。数学美的简洁性,不是人为的简单规定,它刻画出大自然的内在属性。数学美的简洁性,并不是指数学内容本身的简洁而主要表现在逻辑结构,表达式的简洁。
数学理论的迷人之处在于能用简洁的方式和优美的方法对大量的彼此毫无联系的个别情况加以描述,并进行分类,揭示现实世界中的量及其关系的规律。如果一个数学理论本身的结构就很繁琐或累赘,人们都难以看下去,何谈用这个理论解决问题。
举几个数学中最简单的应用简洁性的例子,代数运算中乘法与幂的运算,就是加法与乘法的简化又如,出于对计算运算中简洁性之考虑,才导致了对数运算方法的产生。另一个典型的例子便是二进制的建立。二进制的产生是从逻辑关系的简洁性考虑的,并由此而导致了电子计算机的出现。
简洁性也是众多数学家追求的目标。当我们谈到一些数学大师们对简洁美的追求时,首先想到的是大数学家高斯。1817年3月,高斯把寻求一种最美和最简洁的二次互反律的证明过程,当成他研究的主要动力。莱布尼茨创立微积分时,引进简洁而方便的微分与积分的符号,获得数学界的普遍接受羡慕沿用至今。着名的数学家傅里叶说过,每一个函数,无论多么复杂,总可以表示为某些简单的基本的函数之和。他在创立“傅里叶级数”时,也进行了简洁性的考虑。
教师在数学教学中,如果能从简洁的角度出发,审视问题的结构,分析问题的特点,转化思考的方向,常常可以获得简洁明快的效果。
例如甲、乙、丙、丁4人互相传球,由甲开始发球,并作为第一次传球,经过4次传球后,球仍回到甲的手中,有多少种不同的传球方法。这样的题可以通过画树形图的方法得到答案,但我们更注重等价转化。用甲-乙表示“甲”把球传给“乙”,则甲-丁-甲-丙-甲,甲-乙-丁-丙-甲都是满足条件的一种传球方式。若用1, 2, 3, 4分别代替甲、乙、丙、丁,把“甲-丁-甲-丙-甲”看成是1, 2, 3, 4排在5个不同的位置上,它等价于用1, 2, 3, 4四个数字组成5位数,要求个位、首位只能排数字1,且任意相邻两位数字不相同,这样的5位数有多少个?此时,千位有3种排法,若百位排1,则十位有3种排法,此时有3×3=9种排法;若百位不排1,则有2种排法,则十位仍有2种排法,此时有3×2×2=12种,共有9+12=21种排法。
这是应用型的题型,它虽然没有考查太多的数学知识,如果没有想到一种简洁的方法去分析问题,初步接触时可能会使我们束手无策,但用字母或者对应相关的元素就把它化成我们熟悉的更为简单的问题,不失去本质,又令人心旷神怡。总之,数学的简洁性对数学发展具有极其重要的作用。
(2)统一性。
一切客观事物都是相互联系的,处在对立统一的矛盾之中,大自然是统一和谐的整体,反映客观事物的数学作为描述大自然的一种语言,必然也是和谐而统一的。数学的统一性正体现了数学知识的部分与部分,部分与整体之间的内在联系和共同规律所呈现的和谐一致性。数学中一些表面看来不相同的概念,定理,法则,在一定的条件下处于一个统一体中。许多不同类型的问题可以用统一的思想方法来解决。统一性是数学家追求的目标之一。从解析几何,微积分的诞生到近代数学的许多重大成果都体现出数学的统一性。例如,在微积分中的定积分,二重积分,三重积分,曲线积分,曲面积分,实质上都是一类特殊和式的极限,从极限理论的高度得以统一。
任何一个学过微积分的人都知道牛顿一莱布尼茨公式,
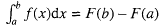
,它将不同的数学概念统一于一个公式,极大的展现了数学微积分这一数学分支内部的统一性。这个公式两边是不同的概念,公式左边
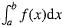
是定积分,它是黎曼和的极限,实质是曲边梯形的面积。而另一端是原函数在积分上下限的差,也是导数的逆运算。
这两边居然可以用等号连接起来,展现了微积分,定积分与不定积分几大运算之间强大的联系,把三者统一于一个公式中,充分体现了数学的统一性。
在讲课过程中,把解析几何与线性代数联系起来,对知识的理解也有很大的帮助,可以使学生对知识了解得更深、更透。如果把解析几何中的三个平面与代数中的三元一次方程组对应起来讲解几何中三个平面的有唯一交点对应用于代数中三元一次方程组的唯一的解。三个平面有唯一交点的条件是三个平面的三个法向量不共面,它对应用于代数中的三元一次方程组的系数行列式不为。这个讲解过程中体现了数学和统一性,展现了数学的和谐美。
运算、变换、函数分别是代数、几何、分析这三个数学分支中的重要概念,但在集合论中,便可统一于映射的概念。数学研究就是从对立统一到新的对立,再到新的统一,螺旋式的上升,不断创新,与时俱进。给我们一种欲穷千里目,更上一层楼的感觉。我们认识了数学中的统一性,就能捕捉住数学中的美点,因此统一性也就成为数学研究的重要方向。
(3)对称性。
对称性被认为是数学美的一个内容,是数学美的又一表现形式,它给人们一种圆满的匀称的美感与感受,其实质是数学中对立统一的概念、运算、命题、图形等在结构与形式方面的体现。对称性是组成某种事物或对象的两个部分的对等性。许多初中同学说,数实在是枯燥无味,计算起来不仅繁琐杂乱,还无聊至极。但事实上,数是在“数学百花园”中最奇妙魔幻的花。我们来看这样一组数据:13²=169, 31²=961;113²=12769, 311²=96721;1113²=1238769,3111²=9678321……同样的数还有一串,如12² = 144, 21² = 441, 112²= 12544, 211² = 44521……至今谁也不知道有多少这类的对称的数。还有一种数自身存在着对称,叫做回文数。99×19= 1881,999×19=18981,9999 × 19=189981, 99999× 19=1899981,99×91=9009, 99×28=2772, 99×82=8118……古希腊毕达哥拉斯学派主张:万物最基本的元素是数,数的和谐就是美。数通过运算让我们感受到简单、整齐、对称、和谐的组合美,令人神往。
着名德国数学家和物理学家魏尔也说过,美和对称紧密相连。数学中的对称性,不仅是一种思想,同时也是一种方法,表现为运用对称的思想来解决问题。使人们对数学的认识提升到另一个更高的层次。在二重积分,三重积分,曲线积分,曲面积分的学习中,如果能巧妙的运用对称性,能达到计算过程简捷的目的。例如,求两个底面半径相同的直交圆柱所围成立体的体积。我们就可以利用对称性,只要求出在第一卦限部分的体积,然后再乘以即得所求的体积。再比如,Ω∈R³,Ω是球心到原点,半径为的球体。计算三重积分
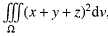
,如果将这个问题直接计算,相当的繁琐,几但如果运算对称性计算,则非常容易的:
这里Ω1为球体在第一卦限的部分,此处就运用了对称性。数学的对称美无处不在,互逆运算也可以看成是对称关系。
除法是乘法的逆运算,指数与对数互为逆运算,因式分解与整式的乘法互为逆运算,这些都可以看成是对称的关系。
(4)奇异性。
奇异性是数学美的另一个重要的特征,也是数学发现中的重要美学因素。任何一个极美的东西都在调和中包含着某种奇异性。奇异是一种美,奇异到极度更是一种美。
数学家看到一些奇异的结果时,如,处处连续不可微的函数等,与看到极其珍奇的艺术品一样震颤。数学领域中一些新概念的产生,都是来自于对奇异美的追求。举一个典型的例子,在1777年的某天,蒲丰邀请了许多朋友做了一个奇怪的试验。他在桌上铺了一张画好一条条等距离平行线的白纸,然后拿出一些质量均匀,长度相等且为平行线间距离一半的小针,让朋友们把这些针随便的扔在白纸上,他在一旁作记录。试验结束后,统计结果一共投了2212次,其中与任一平行线相交有704次。蒲丰发现,投的次数2212约是704的3.142倍,这个近似值是圆周率的近似值,他还说,这个值会随着投的次数的增多,结果越精确,会越来越接近圆周率。这种计算二的方法充分显示了数学方法的奇异美。
康托集也是一个奇异美的例子,集有许多奇异的性质,它是一个无处稠密集,即在任意一个实区间中都包含一个没有集合的元素的子空间。
数学美还具有客观实在性,它是随着人类数学实践活动的发展产生的,具体表现在主体在数学活动中审美心理和所创造的成果中。审美的基础是实践,主体产生审美感觉和人化了的自然界是分不开的。也就是说,人类在实践过程中,一方面,主体的感觉相应地被人化而产生审美感觉,同时,外部自然界被人化而成为美的对象。从人类历史发展来看,主体的审美感觉和客观世界的症状,是人类改造世界的实践成果在主体和客体,内在和外在两个方面的表现。数学美正像雕刻的美,它没有绘画或音乐的那些华丽的装饰,是一种冷而严肃的美。这里肯定了数学美的存在性,数学是真和美的统一。数学并不是唯美的追求美,或者说数学美并不是人为的,而是在逻辑的真假判断与实践的价值判断的统一中追求美。数学美的内容具有音乐,文学作品所具有的那种实在,不是物理世界的实在。从文化传统上看,数学美的实在性更明显。一方面人类文化传统对数学的发展产生极大的影响,人们出生在某种环境中,这种环境制约着他们接受某种特定的数学系统。另一方面,数学也积极的影响着人类文化的发展。例如,古希腊数学中的点、线、面、数,都是对现实的理想化和抽象,它们在文化中也留下了深深的烙印。从哲学,建筑,文学作品和雕刻艺术中,都可以看到数学美的这种实在性。
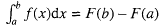 ,它将不同的数学概念统一于一个公式,极大的展现了数学微积分这一数学分支内部的统一性。这个公式两边是不同的概念,公式左边
,它将不同的数学概念统一于一个公式,极大的展现了数学微积分这一数学分支内部的统一性。这个公式两边是不同的概念,公式左边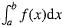 是定积分,它是黎曼和的极限,实质是曲边梯形的面积。而另一端是原函数在积分上下限的差,也是导数的逆运算。
是定积分,它是黎曼和的极限,实质是曲边梯形的面积。而另一端是原函数在积分上下限的差,也是导数的逆运算。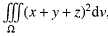 ,如果将这个问题直接计算,相当的繁琐,几但如果运算对称性计算,则非常容易的:
,如果将这个问题直接计算,相当的繁琐,几但如果运算对称性计算,则非常容易的: