洛必达法则论文范文第三篇:探讨一元函数微积分中洛必达法则的教学方式
摘要:探讨一元函数微积分中洛必达法则的教学方式。针对洛必达法则适用题型多, 但计算烦琐、易出错的特点, 举例并归类说明不同类型题目如何正确使用法则。
关键词:微积分;洛必达法则;未定式极限;
基金:上海电机学院学科建设项目资助 (16JCXK02);
一元函数微积分中求极限是很重要的一部分内容。求极限的几类方法中, 洛必达法则是其中很有效、适用范围较广的一类方法。该法则内容简单, 但数学题目千变万化, 在多年的教学实践中发现, 学生在应用洛必达法则求极限中依然存在很多问题。

一、洛必达法则介绍
定理 (洛必达法则) 设: (1) 当x→0时, 函数f (x) 及F (x) 都趋于零;
(2) 在点a的某邻域内 (点a本身可以除外) , f' (x) 及F' (x) 都存在且F' (x) ≠0;

当x→∞时, 以及x→a时, 该法则仍然成立。
洛必达法则本身表达简洁, 使用方便, 适用的题型较多。然而依据多年教学经验, 发现学生解题过程中依然有很多问题, 比如, 不知道和其他方法结合使用, 导致解题困难;不知道恰当整理每次的结果, 再次使用洛必达法则而导致解题失败等原因。举例如下:
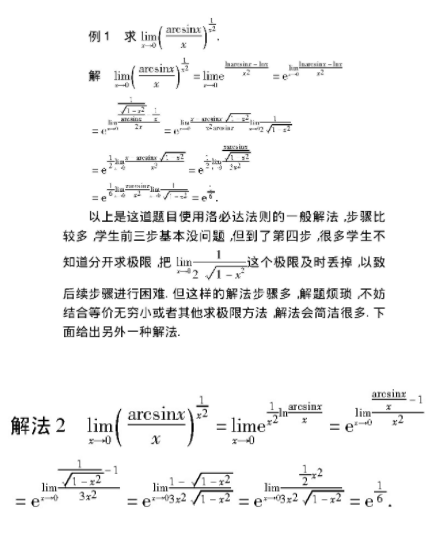
解法2先用等价无穷小代换, 再用洛必达法则, 相比解法1, 步骤明确简洁。因此, 洛必达法则需合理结合其他求极限方法使用。
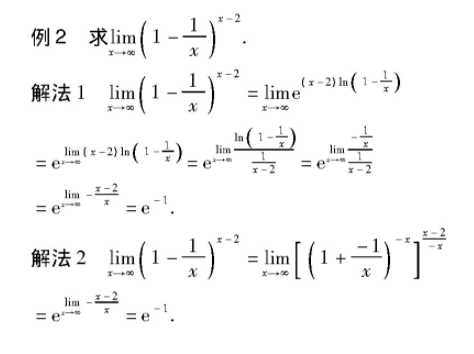
以上用两种基本方法求解了例2, 解法1是洛必达法则结合等价无穷小代换, 解法略烦琐;解法2是用两个重要极限公式求解, 非常简洁明了, 步骤很少, 易于看懂。因此, 例2就不适合用洛必达法则求解, 两个重要极限才是合适的选择。

通过上面的分析, 学生要会熟练灵活地运用洛必达法则求解函数的极限, 必须对其条件、结论全面地了解、掌握, 在学习过程中多加练习。学会结合其他求极限方法, 学会整理每一次求解结果, 知道有些题目即使满足洛必达法则的条件, 洛必达法则也不适用, 甚至无法求解。
参考文献
[1]同济大学数学系高等数学第7版[M].北京高等教育出版社, 2014.
[2]袁建军,欧增奇。高等数学中用洛必达法则求极限需注意的问题[J].西南师范大学学报(自然科学版), 2012 (6) :241-244.
[3]雛志江。应用洛必达法则中常见问题分析[J].山西大同大学学报(自然科学版) , 2008 (5):11-13.





