摘要:为了分析新三维离散系统的动力学行为,丰富混沌遮掩保密通信的理论成果,应用分岔理论和数值方法,绘出了系统随参数变化的分岔图,同时利用Metican小波函数对新三维混沌系统进行控制。发现系统具有丰富的动力学行为(周期运动、准周期运动以及混沌运动),并且小波函数能够将新三维离散混沌系统控制到不同的周期轨道。
关键词:三维离散系统; 动力学; 小波函数; 混沌控制;
Abstract:In order to analyze the dynamical behavior of a new three-dimensional discrete system and enrich theoretical results of chaotic masked secure communication,we apply the bifurcation theory and numerical method to draw out the system' s bifurcation diagram with parameter change,and the new three-dimensional discrete chaotic system is controlled by using the Metican wavelet function. We find the system has copious dynamical behavior( the periodic,quasiperiodic and chaotic motions),and wavelet function can control the new three-dimensional discrete chaotic system to different periodic orbits.
Keyword:a three-dimensional discrete system; dynamics; the wavelet function; chaos control;

0 引言
自1963年气象学家Lorenz提出著名的Lorenz系统[1]以来,大量的混沌系统相继被提出,其中具有代表性的连续系统有Chen系统[1]、Lü系统[1]等,离散系统有Logistic映射[2]、Hénon映射[2]等。对离散系统的研究目前主要集中在二维系统的动力学分析、同步控制及应用方面[3,4,5,6,7],对高维离散系统的研究较少,然而现实生活中,利用高维离散系统能够解决许多实际问题,尤其是在图像加密中具有重要的应用价值[8,9],为此研究高维离散系统的动力学及混沌行为是必要的。
混沌控制是混沌应用的前提。1990年,Ott等[10]提出了利用参数微扰法进行混沌控制,这种方法也被称为是OGY方法,但是此方法的缺点是以局部线性化为基础,控制过程中存在误差。此后,混沌控制问题一直是混沌研究的一个热点[11,12,13,14,15,16],一些混沌控制方法被相关学者提出,例如自适应控制法[13],滑膜控制法[14],模糊逻辑控制法[15],神经网络控制法[16],等等,这些方法为精确地实现混沌的控制与同步奠定了基础。
基于以上考虑,本文基于Hénon映射为基础,通过增加非线性项的方法,给出了一个三维离散系统,该系统共有12个项,其中含有7个非线性项,并研究了系统丰富的动力学行为,同时对系统的混沌行为利用Metican小波函数进行了控制,将系统的混沌运动控制到周期运动,本文的研究成果混沌遮掩保密通信技术具有重要的理论意义。
1 新三维离散系统
本文给出的新三维离散系统是一个三元二次迭代方程组,其动力学方程为

其中a、b为系统参数,取定参数b=0.3,当参数a∈[-0.3,0.4]时,绘制出系统(1)的分岔图,并通过分岔图分析系统的动力学行为,变量xn随参数a变化的分岔图如图1所示。
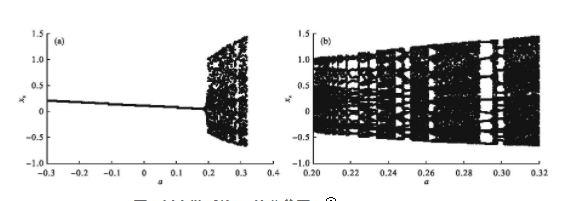
图1 新离散系统(1)的分岔图
从图1(a)可以看出,当参数a∈[-0.3,0.2)时,系统(1)处于周期运动,当a∈[0.2,0.32]时,系统(1)进入混沌区域,从图1(b)可以看出,在混沌区域内,有许多周期窗口,系统在混沌与周期运动之间交替运动。
取初值条件为x0=0.7,y0=0.3,z0=0.4,参数b=0.3时,给出了系统(1)在a的不同取值下的相图。
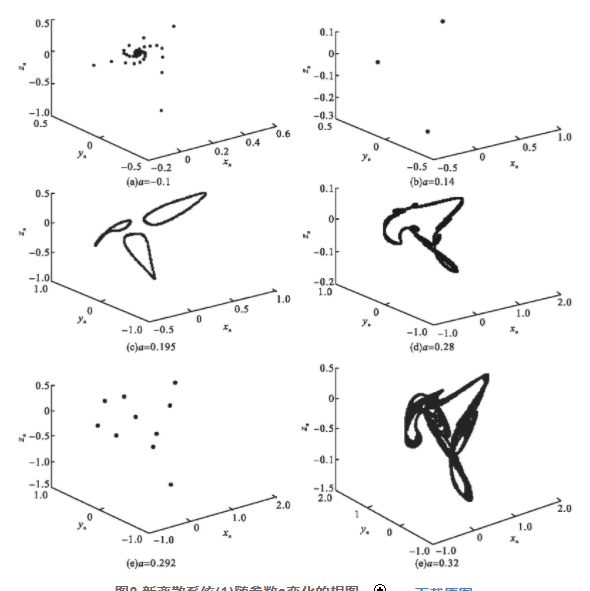
图2 新离散系统(1)随参数a变化的相图
从图2可以看出,当参数a=-0.1时,系统(1)稳定于平衡点,系统处于静止状态(如图2(a)所示);当参数a=0.14时,系统(1)稳定于周期三运动(如图2(b)所示);当参数a=0.195时,系统(1)的周期三失稳,出现三条闭合曲线(如图2(c)所示);当参数a=0.28时,系统(1)处于混沌运动状态,具有如图2(d)所示的混沌吸引子;当参数a=0.292时,系统(1)又处于周期十运动(如图2(e)所示),当参数a=0.32时,系统(1)处于混沌运动状态,具有如图2(f)所示的混沌吸引子。在混沌区内随着参数a的不断增大,周期运动与混沌运动交替出现,这与从图1所示的分岔图中得到的结论是一致的。
2 新三维系统的混沌运动
根据非线性系统的线性化方法,可得系统(1)的雅可比矩阵为
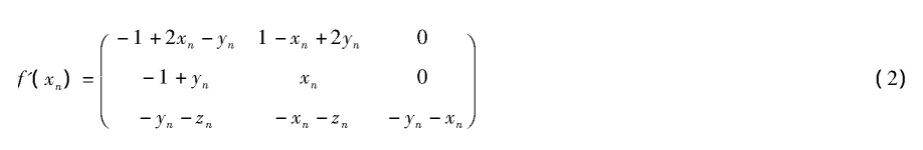
设

将矩阵J的3个特征值求模,得到由大到小的排列为

系统(1)的Lyapunov计算公式为

其中k=1,2,3.
根据系统(1)的Lyapunov计算公式为(5),当系统参数a=0.32,b=0.3,初值条件为x0=0.7,y0=0.3,z0=0.4时,系统(1)的Lyapunov指数谱为(0.167 0,-0.410 0,-0.428 3),有一个大于零的Lyapunov指数,说明系统(1)在参数a=0.32,b=0.3处于混沌运动状态。
同样在系统参数a=0.32,b=0.3时,针对两组不同的初值条件x0=0.7,y0=0.3,z0=0.4和x0=0.700 01,y0=0.3,z0=0.4,考察系统对初值的敏感依赖性。
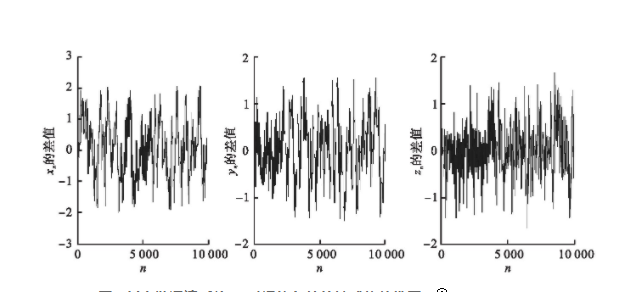
图3 新离散混沌系统(1)对初值条件的敏感依赖性图
从图3可以看出,对于初值条件的微小差异,系统的运动轨迹大相径庭,进一步说明当系统参数a=0.32,b=0.3时,系统(1)处于混沌运动状态。
3 小波函数迭代控制
小波函数具有振荡性,随着自变量在正负方向的不断延伸,小波函数快速衰减,因此其具有很强的收敛性,用小波函数进行混沌控制,能够抑制系统的混沌行为,Metican小波函数的数学表达式为
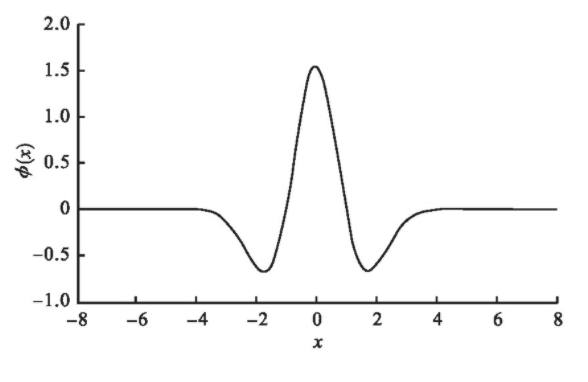
图4 Metican小波函数的图像
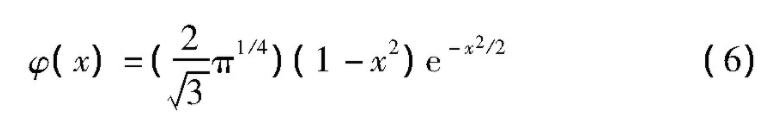
其图像如图4所示。Metican小波函数不具有正交性和尺度函数,但在时域和频域上具有很好的局部化性质,同时满足在全体实数区间上的无穷积分为零。
本文选择Metican小波函数对系统(1)进行混沌控制,为了得到更多的控制结果,将小波函数的系数设为增益系数k,通过调节增益系数k的值,实现对系统(1)的各种控制,用小波函数分别乘以第一个和第二个方程,得到受控的迭代方程组为
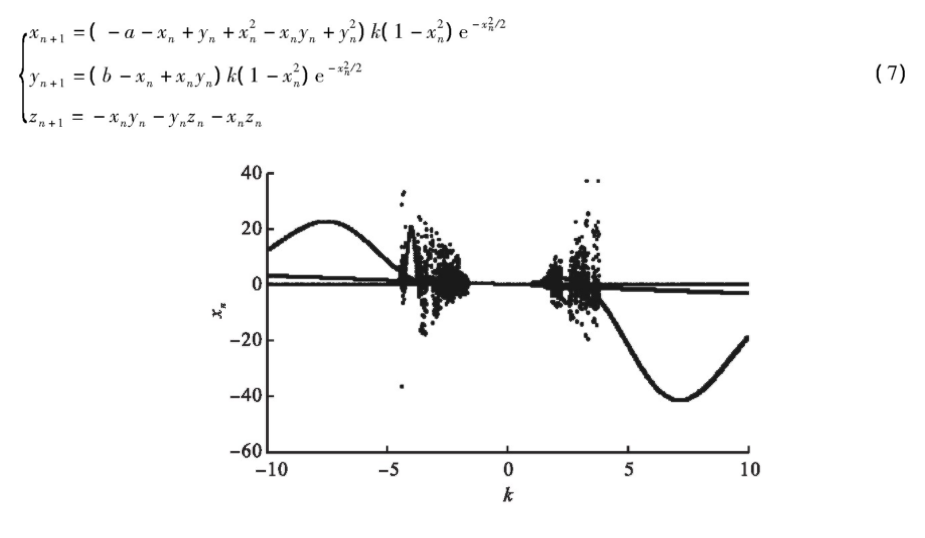
图5 Metican小波函数控制下系统(1)分岔图
将系统参数和初值条件取为a=0.32,b=0.3,x0=0.7,y0=0.3,z0=0.4时,系统(7)关于增益系数k的分岔图如图5所示。
从图5可以看出,通过小波函数,可以将系统控制到周期轨道,同时也能将系统控制到混沌轨道等,可以看出当k=0.1时,小波函数能将系统控制到周期一运动,当k=5时,小波函数能将系统控制到周期三运动,当迭代次数n=2 000时,打开控制开关实施控制,小波函数控制的结果如图6所示。
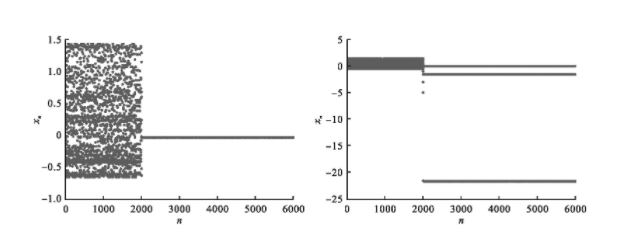
图6 小波函数控制下系统(1)的迭代次数序列图
4 结论
由于众多实际问题能够用高维离散系统来描述,所以研究高维离散系统的动力学行为及其混沌控制是非常必要的。本文给出的三维离散系统具有丰富的动力学行为:周期运动、准周期运动以及混沌运动等。通过Metican小波函数仅对三维离散系统的两个变量进行了控制,在不同的反馈增益系数下,能将三维离散混沌系统控制到不同的周期轨道。
参考文献
[1]陈关荣,吕金虎。Lorenz系统族的动力学分析、控制与同步[M].北京:科学出版社,2003.
[2]刘秉正。非线性动力学[M].北京:高等教育出版社,2004.
[3]刘晓君,李险峰,何万生,等。二维三次方离散系统的混沌控制与广义混沌同步[J].河北师范大学学报(自然科学版),2010,34(4):406-410,416.
[4]Gao J,Gu C G,Yang H J,et al.Prediction of spatial distribution of invasive alien pests in two-dimensional systems based on a discrete time model[J].Ecological Engineering,2020,143:105673.
[5]崔明章,王光义,任国瑞,等。新二维离散超混沌映射及其在图像加密的应用[J].杭州电子科技大学学报(自然科学版),2016,36(3):6-11,17.
[6]刘明明,夏铁成,王金波。带有三角函数的二维分数阶离散系统的混沌现象[J].上海大学学报(自然科学版),2019,25(2):222-226.
[7]Zhao D,Li Y Y,Ahn C K,et al.Optimal state and fault estimation for two-dimensional discrete systems[J].Automatica,2020,115:108856.
[8]王凤英。基于高维混沌离散系统的动态密钥3DES算法[J].微电子学与计算机,2005,22(7):120-123,126.
[9]潘勃,李骞,冯金富,等。一种新的离散混沌同步保密通信方案[J].计算机应用,2010,30(1):198-202.
[10]赵明成,朱洪波,贾琛霞。OGY法控制Henon系统混沌的研究[J].机械,2010,37(10):26-28.
[11]Liu W Y,Cai D H.Bifurcation,chaos analysis and control in a discrete-time predator:Prey system[J].Advances in Difference Equations,2019,2019(1):11.
[12]党红刚,刘晓君。一个混沌复系统的同步与混沌控制[J].四川大学学报(自然科学版),2013,50(5):1049-1052.
[13]Vaidyanathan S,Volos C.Analysis and adaptive control of a novel 3-D conservative no-equilibrium chaotic system[J].Archives of Control Sciences,2015,25(3):333-353.
[14]Singh J P,Roy B K.Second order adaptive time varying sliding mode control for synchronization of hidden chaotic orbits in a new uncertain 4-D conservative chaotic system[J].Transactions of the Institute of Measurement and Control,2018,40(13):3573-3586.
[15]Ahn C K.Fuzzy delayed output feedback synchronization for time-delayed chaotic systems[J].Nonlinear Analysis:Hybrid Systems,2010,4(1):16-24.
[16]Ahn C K.Neural network H∞chaos synchronization[J].Nonlinear Dynamics,2010,60(3):295-302.





