摘要:针对柔性空间索网天线的非线性特点,建立了基于参变量变分描述索网拉压非线性和共旋列式描述几何非线性的有限元控制方程,应用Lemke与改进牛顿法进行求解。通过对索网预张力平衡计算,证明改进牛顿法比Newton-Raphson法具有更强的收敛能力。进一步将力密度法迭代原理与有限元法结合应用于索网天线的非线性找形分析中,获得了理想的索网构型。本文的索网找形方法可广泛应用于空间索网天线结构的设计。
关键词:索网天线; 参变量变分; 共旋列式; 改进牛顿法; 找形分析;
Abstract:In view of the constitutive nonlinearity and geometric nonlinearity of the cable-network antenna, the parametric variational principle and a co-rotational formation were introduced to establish the finite element governing equation.The improved Newton method was employed to solve the governing equation.Firstly,the method was applied for pretension balance calculation of cable-network antenna.The analysis results show that the improved Newton method has a better convergence than Newton-Raphson method.Further,the iterative principle of force density method combined with this finite element method was applied for nonlinear form-finding analysis of the cable-network antenna and an ideal configuration was obtained.The output of this paper is expected to provide some valuable information for studying other similar structures in the future.
Keyword:cable-network antenna; parametric variational principle; co-rotational formation; improved Newton method; form-finding analysis;

1 引 言
空间可展开索网天线的设计中,需要面临众多的问题与挑战。其中,为适用高频率和宽频带的工作要求,需要索网天线在大口径的设计前提下同时具备较高的形面精度,因而索网天线的形面设计是天线设计中的一项重要工作[1,2,3].
国内外学者对索网天线的找形设计开展了大量的研究工作。力密度法[4]是应用最为广泛的线性找形方法,在力密度法基础上,Morterolle等[5]发展了等张力结构的迭代算法,Yang等[6]提出了基于力密度法的找形与找力相结合的优化迭代方法,Liu等[7]对力密度法进行了改进,提高了计算效率。一些学者还发展了其他线性找形方法,范叶森等[8]提出了索网天线等张力找形设计的坐标迭代算法,该方法可使索网张力具有较好的均匀性;杨东武[9]研究了以形找力的极小范数法;李刚等[10]基于平衡矩阵奇异值分解法和线性规划方法,求解了索网抛物面最优预拉力配置。
在线性找形过程中,通常假设索网与桁架连接节点为不动点,不考虑索网与桁架的变形耦合效应。事实上,桁架在索网预张力作用下会产生变形,桁架结构的变形又导致索网节点位置偏离理想位置,降低了索网天线的形面精度。有限元法可实现索网与桁架结构的一体化建模分析,狄杰建等[11]提出了将遗传算法与有限元法相结合的索段预张力优化设计与形面调整方法。谭述君等[12]针对索网天线中张拉索拉压非线性的特点,将参变量变分原理应用于周边桁架式索网天线[13]的有限元分析,提高了绳索数值计算的稳定性。上述有限元法在描述柔性索网结构的几何非线性时采用TL列式和NR迭代法进行求解,但TL法在大挠度下存在计算精度和收敛速度均不高的问题[14,15],而NR法具有收敛的性质,当给定的索网天线初始构型和预张力不够理想,迭代过程中的收敛性将难以保证。
本文基于参变量变分和共旋列式描述索网天线张拉索的拉压非线性和几何非线性,建立含预应力索网结构的非线性有限元控制方程,克服了TL列式在计算效率和精度上的不足,并保留了参变量变分计算张拉索稳定的特点。为提高索网天线计算的收敛性,采用改进牛顿法对控制方程进行求解。进一步,将力密度迭代原理与有限元法相结合,对索网天线进行找形分析。结果表明,所采用的方法具有较好的收敛性和找形精度,可应用于索网天线的形面设计。
2 有限元控制方程及求解理论
2.1 索网本构关系的参变量描述
索网天线的张拉索只能抗拉不能抗压,在存在初始预张力下,其本构关系可表示为
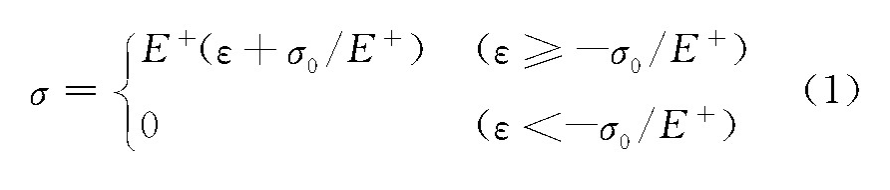
式中 E+为张拉索抗拉模量,ε为轴向应变,σ为轴向应力。
针对式(1)引入参变量λ,可将式(1)统一表述为
σ=E+(ε+σ0/E++λ) (2)
式中 λ满足
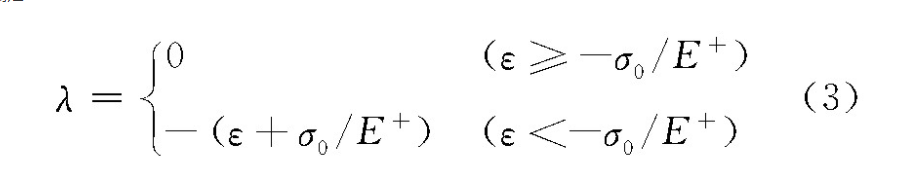
引入非负的松弛变量ν,可得绳索的拉压状态控制方程为
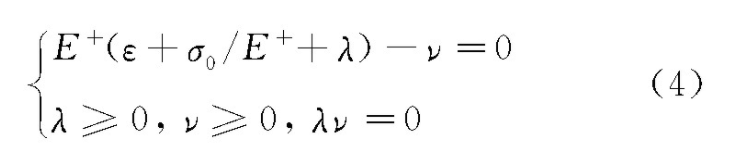
式中 λ ν=0是互补条件,当λ=0,ν=0时,绳索处于未变形状态;当λ>0,ν=0时,绳索处于受压状态;当λ=0,ν>0时,绳索处于拉伸状态。
2.2 参变量与共旋列式的统一描述
采用共旋列式描述索单元的几何非线性,共旋列式在大挠度、大转角、小应变分析时具有更简洁的列式和更高的计算效率。结合参变量与共旋列式的索单元切线刚度矩阵可表述为
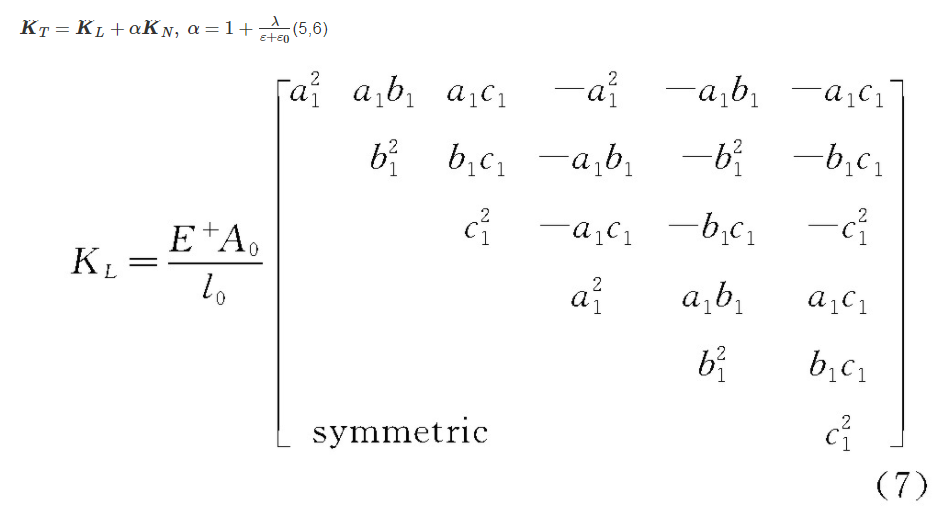
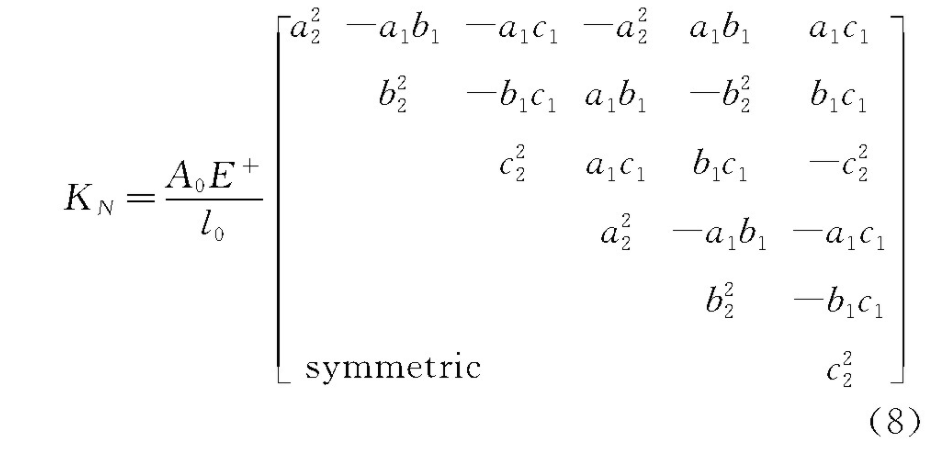
式中 ε为当前构型下的应变,ε0为绳索初始预张力下的应变。A0和l0是索单元的截面积和初始长度,定义α,β和γ为当前构型下单元与总体坐标系x,y和z轴的夹角,a1和a2是α的余弦和正弦,b1和b2是β的余弦和正弦,c1和c2是γ的余弦和正弦。
将各个索单元的刚度矩阵KT、参变量λ和互补变量ν等进行组装,可得索网非线性有限元的控制方程为
[ΔP]=[KT]{Δδ} (9)
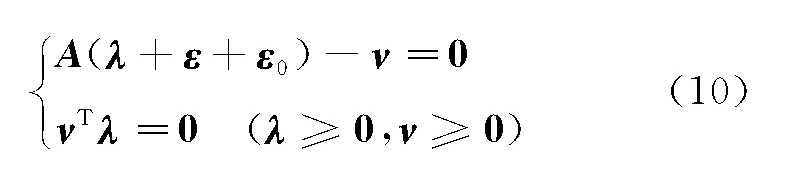
式中 A为diag(E+i),λ为diag(λi),ε为diag(εi),ε0为diag(ε0 i),ν为diag(νi),i为对应的第i索单元。式(10)是一个线性互补问题,本文采用经典的Lemke算法求解。
2.3 非线性有限元方程的改进牛顿法
NR法是求解式(9)最常用的迭代方法,通过线性逼近和反复迭代直至收敛于实际的平衡路径,其迭代格式为
[KT]i{Δδ}i +1={ΔP}i
{δ}i +1={δ}i+{Δδ}i +1 (11)
式中 [KT]i为第i次迭代时的切线刚度矩阵,{Δδ}i +1为第i次迭代时由节点不平衡力引起的位移增量,{ΔP}i为第i次迭代时的节点不平衡力,{δ}i为第i次迭代时的节点位移。
由于NR法是局部收敛的,当给定的初始预张力不在索网平衡状态附近时,迭代计算往往存在收敛困难。为了放宽对初始值的选择要求,将NR法与线性搜索方法结合使用,迭代公式为
{δ}′i +1=(1-2 -k){δ}i+2 -k{δ}i +1 (k=0,1,2,…) (12)
式中 k为松弛因子,k值的选取需满足
|{ΔPi??+1}|<|{ΔPi}| (13)
当k=0时,{δ}′i +1={δ}i +1,此时该方法退化为NR法;当k→∞时,{δ}′i +1={δ}i,此时迭代步长趋近于0.k值越大,收敛域就越大,可有效克服NR法初始值要求苛刻的缺点,但k值越大,迭代步长越短,将导致收敛的速度越慢。为了避免收敛速度过慢,本文在计算过程中给定了k值的上限,当k值达到上限且不满足式(13)时,仍然转至下一个迭代步。
3 索网预应力平衡的有限元计算
根据上述理论在Matlab平台编制非线性有限元程序,应用该程序对图1所示模块化天线单个模块的抛物面索网进行预应力平衡计算,单个模块的初始边长约为2600 mm.模型共有181个节点,408个单元。索网采用抗拉模量为20 GPa的凯夫拉绳,直径为1 mm;计算中约束背索网主径向的节点;为验证参变量变分与改进牛顿法相结合的有限元法在求解索网大变形下的计算稳定性,给定索网天线前后索网及纵向索网20 N张紧力;要求索网的收敛精度满足‖ΔP‖<0.1,分别采用NR法和改进牛顿法进行求解,为兼顾计算效率,改进牛顿法中k值上限取5.
经计算,NR法在迭代过程中无法收敛,而改进牛顿法经过215个迭代步计算后,达到‖ΔP‖<0.01的收敛要求。图2为两种方法在前215个迭代下的‖ΔP‖值,说明NR法的节点不平衡力在120 N附近振荡,始终无法收敛。而改进牛顿法虽然无法保证每个迭代步都是收敛的,但计算总趋势是收敛的。此外,改进牛顿法计算用时12.37 s,仍具备较高的计算效率。

图1 天线索网及整体结构
Fig.1 Structural configuration of cable -network antenna
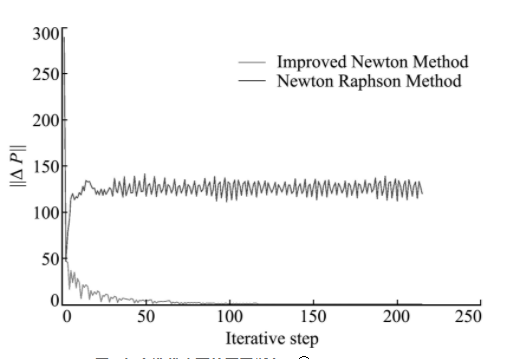
Fig.2 Unbalance force at each iterative step
图3为索网的内力云图,索单元的最大内力为40.9134 N,最小内力为0 N,说明在索网达到新的平衡态后部分索单元出现了松弛。
4 索网天线的找形分析
基于参变量原理的有限元法较强的收敛能力为应用于索网天线非线性找形设计提供了必要条件。索网找形设计还要求满足所有前索网节点均在理想抛物面上;索网单元不出现松弛,内部索段张力相等;索网的形面精度、垂跨比满足设计要求等。在等张力迭代力密度法中,对于给定成形张拉力T0和本次迭代所得的索段长度li情况下,可设定迭代力密度值为qi +1=t0/li.本文将该力密度法迭代思想与参变量变分有限元法相结合,实现给定张力下的找形设计。具体实施步骤如下。
(1) 设计初始索网拉力T0.
(2) 基于参变量变分有限元法计算索网节点坐标及索单元拉力。
(3) 修正索网节点坐标至抛物面上,并计算前索网节点坐标更新前后误差t ol、垂跨比ρ和形面精度δ。
(4) 判断ρ,t ol和δ等指标是否满足要求。是,输出节点位置和索网拉力,结束分析;否,更新索网坐标,并更新拉力至T0,返回至步骤(2)重新进行迭代。
给定索网天线前后索网中的边界索网90 N张紧力,内部索网10 N张紧力和纵向索网5 N张紧力。要求索网的垂跨比、形面精度和索网节点更新收敛误差分别满足ρ<0.1,δ<0.5 mm和t ol<0.001 mm的设计指标,其中形面精度定义为δ≈l2/f C2,l为前索网索段长度,f为天线焦距,C =7.872.在满足上述指标下,获得了图4所示的有限元法找形结果。将该有限元法的计算结果与传统的力密度法计算结果进行对比,两种方法下前索网和竖向索网的内力分布如图5所示,可见两种方法的索网内力一致性较好,说明本文所采用的计算方法是可行的,而且本文所采用的有限元法获得索网内力分布具有较好的均匀性。
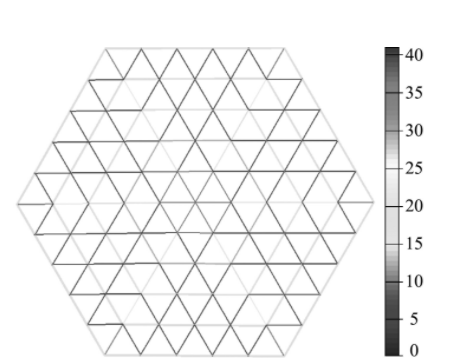
图3 索网内力云图
Fig.3 FEM analysis results of cable -network antenna
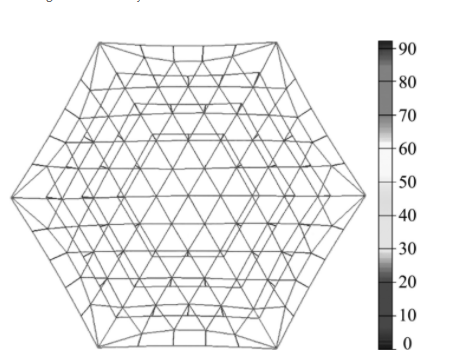
图4 找形后的索网构型
Fig.4 Internal force distributing pictures of form-finding results of cable-network antenna
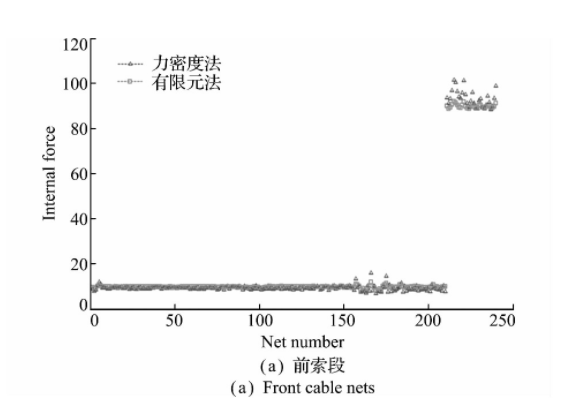
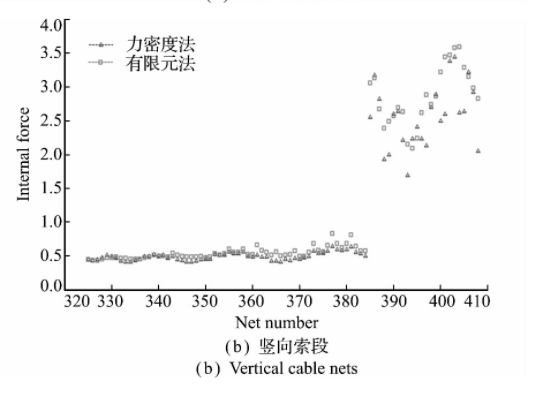
图5 前索网各索段内力分布
Fig.5 Distributing of internal force of front cable -network
5 结 论
针对大柔性索网天线拉压非线性和几何非线性的特点,为提高算法的稳定性和收敛效率,建立基于参变量变分和共旋列式结合的非线性有限元控制方程,采用Lemke算法和改进牛顿法进行求解。将该有限元法应用于索网的预张力平衡计算和索网的找形设计。通过分析,可得到如下结论。
(1) 本文所采用的改进牛顿法比NR法具有更好的收敛性,同时兼顾了计算效率,适用于大变形下的索网预张力平衡计算。
(2) 将有限元法与力密度法迭代原理相结合,应用于索网找形分析,获得了理想的索网构型,与力密度法计算结果进行对比,证明该找形方法是可行的。
(3) 本文的索网找形方法可进一步推广至柔性边界下的索网找形设计和预张力优化。
参考文献
[1] 段宝岩。大型空间可展开天线的研究现状与发展趋势[J].电子机械工程,2017,33(1):1-14.(DUAN Bao -yan.The state -of-the -art and development trend of large space -borne deployable antenna [J].Electro -Mechanical Engineering,2017,33(1):1-14.(in Chinese))
[2] Tibert A G,Pellegrino S.Review of form-finding methods for tensegrity structures [J].International Journal of Space Structures,2003,18(4):209-223.
[3] 寻广彬,吴志刚,彭海军,等。大型索网天线机电耦合动力学建模与主动变形控制[J].计算力学学报,2016,33(4):570-575.(XUN Guang-bin,WU Zhi-gang,PENG Hai-jun,et al.Electromechanical coupling dynamic model and active shape control of large cable-network antenna[J].Chinese Journal of Computational Mechanics,2016,33(4):570-575.(in Chinese))
[4] Linkwitz K.Formfinding by the "direct approach" and pertinent strategies for the conceptual design of prestressed and hanging structures[J].International Journal of Space Structures,1999,14(2):73-87.
[5] Morterolle S,Maurin B,Quirant J,et al.Numerical form-finding of geotensoid tension truss for mesh reflector [J].Acta Astronautica,2012,76:154-163.
[6] Yang G G,Duan B Y,Zhang Y Q,et al.Uniform-tension form-finding design for asymmetric cable -mesh deployable reflector antennas [J].Advances in Me -chanical Engineering,2016,8(10):168781401667236.
[7] Liu W,Li D X.Simple technique for form-finding and tension determining of cable-network antenna reflectors [J].Journal of Spacecraft and Rockets,2013,50(2):479-481.
[8] 范叶森,李团结,马小飞,等。一种等张力空间索网结构找形方法[J].西安电子科技大学学报(自然科学版),2015,42(1):49-55.(FAN Ye -sen,LI Tuan-jie,MA Xiao -fei,et al.Form-finding method of equal tension cable networks for space mesh antennas [J].Journal of Xidian University,2015,42(1):49-55.(in Chinese))
[9] 杨东武。星载大型可展开索网天线结构设计与型面调整[D].西安电子科技大学,2010.(YANG Dong-wu.Structure Design and Profile Adjustment of Large De -ployable Mesh Antenna for Satellite[D].Xidian University,2010.(in Chinese))
[10] 李刚,关富玲。环形桁架可展天线抛物面索网的预拉力优化[J].浙江大学学报(工学版),2005,39(10):1557-1560,1643.(LI Gang,GUAN Fu-ling.Pretension optimization in parabolic cable net of astromesh deployable reflector[J].Journal of Zhejiang University(Engineering Science),2005,39(10):1557-1560,1643.(in Chinese))
[11] 狄杰建,段宝岩,杨东武,等。索网式星载展开天线结构纵向调整索数计初始张力的优化[J].机械工程学报,2005,41(11):153-157.(DI Jie -jian,DUAN Bao -yan,YANG Dong-wu,et al.Optimization on initial cable tensions and number of cables for a cablenet deployable spaceborne antenna[J].Chinese Journal of Mechanical Engineering,2005,41(11):153-157.(in Chinese))
[12] 谭述君,侯健,吴志刚,等。索网天线的参变量变分及非线性有限元方法[J].力学学报,2014,46(5):770-775.(TAN Shu-jun,HOU Jian,WU Zhi-gang,et al.The parametric varational principle and non -linear finite element method for analysis of astromesh antenna structures [J].Chinese Journal of Theoretical and Applied Mechanics,2014,46(5):770-775.(in Chinese))
[13] Thomson M W.The astromesh deployable reflector,antenna and propagation scoiety[J].IEEE International Symposium,1999(3):1516-1519.
[14] Wempner G.Finite elements,finite rotations and small strains of flexible shells[J].International Journal of Solids and Structures,1969,5(2):117-153.
[15] Crisfield M A,Moita G F.A unified co -rotational framework for solids,shells and beams[J].International Journal of Solids and Structures,1996,33(20-22):2969-2992.





