投资风险分析探讨的是随机因素对经济评价指标所产生的作用关系,根据该结果围绕经济评价指标作出概率描述,是现阶段方案风险分析领域的重要途径。基于投资风险分析而衍生出的方法形式多样,其中蒙特卡罗模拟法则颇为典型,其具有适用范围广、结果精度高等多重优势。

一、蒙特卡罗模拟法概述
1. 概念叙述
蒙特卡罗(Monte Carlo)模拟法,又称随机抽样或统计试验方法,属于计算数学的范畴,最初为满足原子能事业的发展而形成,并逐步演变至今。传统的经验方法存在精准度不足的局限性,其难以逼近真实物理过程,所得结果缺乏参考价值。而蒙特卡罗模拟法通过以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解,可增强模拟结果与实际情况的一致性,有利于后续分析工作的顺利展开。为象征性地表明这一方法的概率统计特征,故借用赌城蒙特卡罗命名。
2. 优点
经验表明,投资经济效果指标受多方面因素的影响,各自的概率分布特征各异,例如存在不对称特性或是产生具有不规则特性的峰值,而采取传统的解析法,将明显增加分析工作量,复杂度也将随之提高。而基于蒙特卡罗模拟法的应用,可省去复杂的数学计算环节,经多次重复抽样试验后即可。
通过计算机技术的融入,赋予蒙特卡罗模拟法更为显著的功能特征:一是便捷性,即无需展开复杂的演算,降低了使用者的门槛;二是高效性,基于蒙特卡罗模拟法的优良应用机制,可以在短时间内完成相应操作,满足现代项目管理对于效率所提出的要求。
3. 适用范围
通常蒙特卡罗模拟通过构造符合一定规则的随机数来解决数学上的各种问题。一般蒙特卡罗模拟在数学中最常见的应用就是蒙特卡罗积分。
受惠于先进信息技术的支持,蒙特卡罗模拟的适用范围逐步扩宽,现阶段在金融工程、生物医学、计算物理学等领域均可见其"身影".
通过蒙特卡罗模拟法的应用能够兼顾多方面的风险因素,将各类因素所具有的不确定性进行转化,通过概率的方式呈现对成本的影响。蒙特卡罗模拟法可视为多元素变化法的代表形式,其各类元素均与风险的不确定性息息相关,突破了传统敏感分析方法的局限性。
二、蒙特卡罗模拟计算流程
蒙特卡罗模拟的实现以抽样理论为依托,对随机变量展开抽样统计,经计算后确定抽样统计特征值,此处所得的结果将作为待解决问题的数值解。基于此方法的应用可确定预测值的区间以及分布特点,对于多要素不确定的问题具有较好的应用效果。
蒙特卡罗模拟法应用于项目进度中,应充分考虑到各活动的时间问题,主要包含如下三方面:
最乐观持续时间(to):在最佳的条件下,保证某项工作可依据要求落实到位所需的最少时间。
最可能持续时间(tm):在正常条件下,保证某项工作可依据要求落实到位可能需要的时间。
最悲观持续时间(tp):在最不利条件下,保证某项工作可依据要求落实到位所需的最长时间。
确定估算值区间,假定所花费的持续时间在该区间呈三角分布的特点,此时可根据如下公式求得期望持续时间:
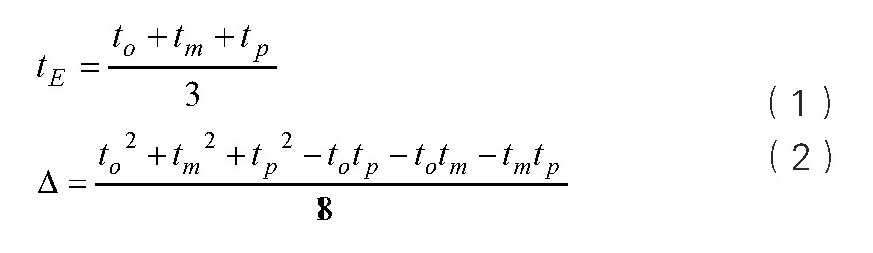
基于工程项目的风险分析本就具有较高的复杂度,若风险发生概率或风险损失的数学公式内还存在某些非初等分布函数时,将进一步增加问题的复杂程度,求解难度随之加大,此时传统方式的适用性将明显不足。而通过蒙特卡罗模拟法的应用,只需求解数学式描述项目风险的发生概率即可,利用计算机以高效率的方式组织多次试验后,所得结果的精度可有所保障,整个流程得以精简。主要按照如下流程依次执行:确定概率数值→生成随机数并抽样→结合数学模型获取结果→创建概率分布图→判断风险度。
三、蒙特卡罗模拟法的实际应用
1. 工程实例
为进一步分析蒙特卡罗模拟法的应用效果,此处结合工程实例展开分析。关于某投资工程项目的基本参数,具体内容为:投资均值100000元、标准差5000元、正态分布,寿命最大值16年、最小值6年、分布类型正态分布,预定利率均值10%,分布类型常数,残值均值1000元、分布类型常数,年度收益均值70000元、标准差4000元、分布类型正态分布,年度支出均值40000元、标准差2000元、分布类型正态分布。
该投资活动中的残值和预定利率为定值,而投资、年度收益、年度支出、寿命期均服从其相关参数的概率分布,本例以净现值(NPV)作为项目经济评价的指标。根据净现值的计算公式应用蒙特卡罗模拟法,经过随机重复抽样试验后取得净现值的抽样分布结果,其能够反映估算的概率密度函数,进而创建频率直方图,根据该图形展开有关于净现值累积概率分布状况的判断。
蒙特卡罗模拟法的应用主要采取计算机工具,以较为自动化的方式高效模拟丰富的随机数,首先将形成具有均匀分布特征的随机数,在此基础上产生服从某一分布的随机数,此后即可进入到随机模拟试验环节。依托于EXCEL工具中的BAND()函数,能够得到随机变量的观测值。若需确定其它形式的概率分布随机变量,此时较为合适的是应用反函数变换技术以及VLOOKUP()等相关函数。模拟法中所罗列出的相关参数性质具有一致性,即反映的是复合投资项目参数概率分布特点的结果。
利用EXCLE产生随机数,主要利用了以下函数:
BAND()放回0≤及<1的均匀分布随机数;
BAND()*(b-a)+a生成a与b之间的随机实数;
INT(BAND()*(b-a)+a)生成a与b间的随机整数(a,b为整数);
NORM INV (RAND(),μ,σ)返回制定平均值和标准差的正态累积分布函数的反函数。
净现值的公式:B 1 2-P V (1 0%,C 2,D 1 2)+P V (1 0%,C 1 2,D 1 2)-PV(10%,C12,1000)
用以上各个公式便可模拟出结果:最大值部分为投资114405、寿命16、年度收益83366、年度支出45507、净现值252445,最小值部分为投资81982、寿命6、年度收益56945、年度支出23723、净现值-8987,均值部分为投资99952、寿命11、年度收益70012、年度支出40001、净现值96463,标准方差部分为投资4920、寿命3、年度收益3906、年度支出1991、净现值45594.
2. 本投资项目的蒙特卡罗模拟分析结果
(1)试验次数及误差。通过对投资、年度支出等相关指标的分析可知,误差均稳定在±3%以内。
(2)经济评价指标分析。净现值是案例工程中所采用的重点经济评价指标,对此创建其分布柱形图。最终可知,净现值呈现出正态分布的特点,而通过对净现值相关数据的分析可知,其均值为96463,标准方差符合正态分布要求。
3. 项目的风险分析
投资盈利(NPV≥0)的概率为92.5%,亏损(NPV<O)的概率为7.5%,大于零的累积概率为0.97.由此说明,该投资项目具有较为良好的抗风险能力。
四、结论
通过蒙特卡罗模拟法的应用,可确定项目经济评价指标在期望值和概率分布方面的具体表现,从而进一步对投资方案的风险情况作出较为科学的判断,作为投资者的重要决策依据。





