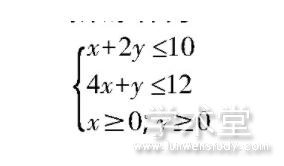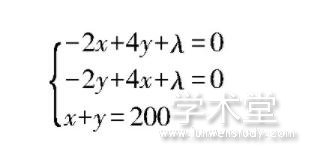生活就像一个大舞台,里面包含万象。而数学知识原本就比较抽象,它不像语文那样具有描述性,也不像美术那样具有观赏性,体育那样具有活动性。数学的各种概念的描述既枯燥又无味,要想使抽象的内容变得具体,易懂,就得从生活中挖掘素材,在日常生活中发现数学知识,利用数学知识,来提高学习的兴趣。下面是数学与生活论文8篇,供大家参考阅读。
数学与生活论文第一篇:日常生活中最优化方法的运用探析
摘要:作为一种理论性、实践性极强的解决问题工具,最优化方法在实际生活中受到广泛应用,具有重要意义。本文在对最优化方法进行论述的基础上,分别从不同学习阶段列举抛物线顶点法、线性规划最值法以及拉格朗日乘数法在实际生活中应用的例子,以期促进最优化方法的应用。
关键词:最优化方法; 实际生活; 应用;
追求最优结果是人人都期待的,最优化方法的出现为人类从大量备选项中找出最优答案提供了一种思路,因而加强最优化方法学习,培养最优化方式思考问题,具有重要意义。随着社会经济的发展,最优化方法受到普遍关注,并被广泛应用于企业经营管理、物流运输网络等各个领域。在实际生活中,利用最优化方法解决问题的例子比比皆是,例如管理人员在企业经营过程中确定合适的商品价格和产量,以追求效益或利润最大化目标,又如消费者购买商品时通过不同的商品组合,以最大程度满足自身期望。最优化方法对实际生活的突出指导意义,要求人们进一步增强对最优化方法的学习了解与实践应用。因此,本文用三种不同例子介绍最优化方法在实际生活中的应用。
1 最优化方法概述
随着现代管理科学的日臻完善,最优化方法作为数学学科中的一项重要内容,在其中扮演着重要理论基础的角色。最优化方法是指决策者为实现人力、物力以及财力的效益最大化,综合运用各种数学工具对待解决问题的众多方案展开深入研究,并做出选择,从而为其做出科学合理的决策提供理论依据。在实际生活中,被广泛应用于经济管理、交通设计等领域。
在具体应用时,最优化方法是在既有约束条件下,找到最佳选择使目标函数取得最大值或最小值,即可分为两种情形:第一,通过寻找最佳的资源要素投入,实现产量最大或利润最高的目标;第二,为达到某一目的,使投入资源要素控制在最少状态。[1]在利用最优化方法解决具体问题时,一般分为四个步骤,即明确求解问题和已知信息、建立相应数学模型、分析求解数学模型、检验结果是否为最优解。
2 最优化方法的实际应用
本文分别列举三个从不同学习阶段习得的最优化方法知识(抛物线顶点法、线性规划最值法、拉格朗日乘数法)在实际生活中的例子,增加人们对最优化方法的应用了解,促进对最优化方法的应用推广。
举例1:抛物线顶点法。
一商店销售某种品牌洗衣液,已知该品牌洗衣液进价为每瓶10元,根据以往销售数据,该品牌洗衣液每天销售量与售价呈以下线性关系,即:Q=40-2X,求商店每天以什么价格销售该品牌洗衣液时利润最大?对应销售量是多少?
利润为收入和成本之差,根据题意可知,设销售价格为X,即可得到关于利润的关系式,即:y=(x-10)(40-2x)。
经过化简后,即得y=-2x2+60x-400,根据抛物线相关知识,不难得到该抛物线开口方向向下,对称轴为x=15,此时求解得到y=50,即该抛物线的顶点坐标为(15,50)。
由此可以知道当商店将该品牌洗衣液定价为每瓶15元时,可获得最大利润50元,此时对应的销售量为10瓶。
举例2:线性规划最值法。
某人以制作A、B两种手工艺品谋生,其中制作1件A手工艺品需要用1个小时,同时用掉2件方木,每件可获利8元;制作1件B手工艺品需要用4个小时,同时用掉1件方木,每件可获利12元。该手工艺者每天工作10个小时,每天方木固定供应12件,求该手工艺者每天制作A、B两种手工艺品各多少件时获利最高?最高可获利多少元?
假设该手工艺者每天制作手工艺品A为x件、手工艺品B为y件,获利为z元。根据题意可知,需要求解获利得公式为:z=8x+12y。对应的线性约束条件为:
由此,本题线性规划求解数学模型已经建立。通过建立平面直角坐标系及研究分析后,不难发现当x=2,y=4时,获利z可取最大值64元。经过验证分析,该解是最优解,即有当该手工艺者每天分别制作A、B两种手工艺品件2件、4件时,可以获得最高收益64元。
举例3:拉格朗日乘数法。
某企业以生产甲、乙两种商品为主,其中每生产1件甲商品可获利2元,每生产1件乙商品可获利3元。根据以往历史生产数据分析,当生产x件甲商品、y件乙商品时,生产总成本C(x,y)与生产甲和乙两种商品的件数具有以下关系:C(x,y)=x2+y2-4xy+2x+3y(元)。已知该企业每天生产甲和乙两种商品的产能之和控制在200台,求当甲、乙两种商品分别生产多少台时企业利润最大?最大利润为多少?
由题意可知,两种商品200台的产能控制即为约束条件,所以约束条件函数为x+y=200。
由此可得到拉格朗日函数F(x,y),进而通过求导求解本题,即F((x,y)=2x+3y-(x2+y2-4xy+2x+3y)+λ(x+y-200),求偏导结果为:
不难解得x=100,y=100,λ=-200。通过进一步计算,可得此时企业利润为20000元。经过分析验证,当甲、乙两种商品均生产100台时,企业可获得最大利润20000元。
通过对上述三个实际例子的讲解说明,更加深入了解了最优化方法在实际生活中的作用,且最优化方法不只局限于这三种,诸如运筹学中最大流等问题的解法都是最优化方法的一种。
3 总结
本文以三个实际例子说明了最优化方法的实践意义,随着科学技术的进步,大量最优化方法可以通过计算机技术求解最佳答案,例如Matlab等软件,这也是未来最优化方法与计算机技术有效结合发展的趋势。[2]同时,本文激励学生加强对最优化方法的学习,培养解决实际问题能力,对未来发展具有重要作用。
参考文献
[1]李顺杰.运筹学与最优化课程教学研究[J].高教学刊,2015(21):64-65+67.
[2]陈征,沈丹红.基于Matlab软件的《最优化方法》教学[J].宁波工程学院学报,2011,23(03):101-103.
数学与生活论文第二篇:生活中数学的趣味性浅析
摘要:数学大师陈省身说,数学是一门有着独特魅力的学科,是一门好玩的学科.数学蕴藏在我们生活的角角落落,帮助我们解决实际生活中的许多问题.数学从来就不是冷冰冰的公式和定理,更不是拒人于千里之外的证明和推导.从初等数学到高等数学的过渡,数学历史背景的融会贯通和数学内涵的点滴渗透,在我脑海中慢慢搭建起数学大厦,作为数学专业的学生,发现数学、思考数学、探究数学是我们的使命也是我们的责任.数学的趣味性在生活中随处可见,自然身边的一些数学现象也能引起我深刻的思考.让我们一起感悟数学学习中一些趣味性思考的快乐.
关键词:数学思考; 趣味数学;
在现实生活中有很多被我们忽视的数学存在,比如,吹出来的气泡为什么是圆的?为什么露水珠不是方形的?生活中这些很小的问题有没有引起你的思考呢?
在通读数学家图灵新知《数学思考法:解析直觉与谎言》一书中,谈到“井盖为何是圆形的”引起我强烈的思考,人们常说圆形井盖不容易掉到井里.真的是这样吗?那其他形状的井盖就真的容易掉下去?面对这种情况,大多数人都会不假思索地认为它本身就是圆的,就像人生下来都两个眼睛一个鼻子一样.人们的思维固定化,总将先入为主这种思想灌入脑后,很少有人静下来深究其原因.因为人们一旦被“井盖是圆形的”这种固有观念植入脑海中,就很难将其剔除掉,思维将很难摆脱其控制.而图灵一步一步分析,得出真相.在书中先以正方形证明,再以长方形证明,后又用等边三角形,图灵将在每一个顶点处将圆规的针尖放置在正三角形的一个顶点上,画出连接另外两个顶点的扇形,得到所谓的“勒洛三角形”这种等宽性满足条件,从而达到目的.书上的每一步具体证明都充满了说服力.图灵的一步步严谨推导和假设,先举特例,继而验证,再得到的“勒洛三角形”,一步步接近完美,因此,井盖是圆的证明油然而生.
而在没有读到这篇文章之前,我对圆形井盖的理解仅仅停留在初中的思维,我相信大部分的人也一样,不会再用已知的知识去推导它,仅仅认为井盖做成圆形更节省材料,便于运输,却没有深入地思考过,也没有严谨证明.这个弊端不得不承认是大部分数学专业学生的诟病.所以平时常见的井盖也蕴含着它的数学规律!作为当今大学生应觉得惭愧的是我们虽然每天学习数学,看似掌握数学.而在生活中我们却很少用数学思维去思考事情,这是当今大学生中普遍存在的现象,也是数学人才培养的弊端.
就拿一个简单的例子,年轻人都爱听歌,耳机对我们来讲并不陌生,使用耳机时每个人都可能遇到过这样的困惑,从包中十有八九会拿出缠成一个疙瘩的耳机.这些看似很寻常的事情,很少有人留心注意.而在一次阅读时我了解到:耳机线在自然状态下由于长而柔软,会自发地形成许多不同的构型,它们总是倾向于自我缠绕,最终结成一团,难以解开.一旦打结,从能量角度上来说就不太可能自动解开了,而且绳子的结只会越来越多.这也难怪我们稍不注意就会遇到这种困惑,经过我的阅读,我又了解到:在大约50%的概率下,耳机线就会打一个结.而影响这一结果的主要因素之一就是耳机线的长度:一般长度小于0.45米打结的情况较少;而随着长度增加,打结的概率也增大.然而这也有上限,当绳子的长度达到1.5米时,它就会充斥整个盒子,一般在超过50%的情况下,都不会打结.
这也间接地告诉我们这种打结问题是可以人为避免的.然而如何减少这种缠绕现象呢?我们可以使用较硬的耳机线,增加它的硬度,打结的概率自然就会减小了;还可以选择较小的容器,就会降低它自发地缠绕.了解了这个原理后,就可以轻松地根据耳机的长度,根据大学所学的概率论知识计算出一个大致的打结概率,既能合理地避免打结现象的发生,也增强了我们的数学专业素养,提高数学应用意识.这些日常现象与数学有着密不可分的联系,而数学家的伟大之处在于面对这些问题时没有回避,用智慧化解,这种学习精神正是值得我们当代青年学习的目标,数学家对数学的浓厚情怀也鞭策我在大学学习中面对问题多思考、勤动脑.
当然,打结可不是一个简单的问题,数学家们为了深入研究它,专门在拓扑学上引入一个分支学科叫作纽结理论,就是用来研究纽结的数学特性.纽结的数学定义是:处在三维空间里的任何简单封闭曲线.耳机线问题迎刃而解,再面对这种纽结问题时便可以见招拆招.
由此可见,生活处处有数学,数学处处得真理.数学就在生活里,生活处处有真理.有次课外阅读时,无意间读到一篇哲理性很强,而又充满数学韵味的故事.正好联系上大学期间正在学习数学分析的内容.故事是这样的,青年问禅师:“大师,我很爱我的女朋友,她也有很多优点,但是总有几个缺点让我非常讨厌,有什么方法能让她改变?”禅师浅笑,答:“方法很简单,不过若想我教你,你需先下山为我找一张只有正面没有背面的纸回来.”青年略一沉吟,掏出一个莫比斯环.禅师拿着青年的莫比斯环说:“正面亦是反面,反面亦是正面.优点和缺点,只是看待的角度方式不同罢了.施主既然知晓这莫比斯环的深意,又何必在意她的小缺点呢?”故事中提到的莫比乌斯环就是在大学数学分析教材中所提到的莫比乌斯带,它的定义为:“只要将一个长方形纸条ABCD的一端AB固定,另一端CD扭转180度后,把AB和DC黏合在一起就可得到一条莫比乌斯带.”
试想学过高等数学的人对它的名字并不陌生,如果沿这个带子上的任一处出发涂以一种颜色,则可以不越过边界将它全部涂遍,当然,这也就说明了它的单侧特征.明明是两个面,却变成了一个面,它真的是一个神奇的存在.这个现象后来被人们称为“怪圈”,然而这个怪圈不仅仅只是具有单侧性这么简单.它蕴含的力量是无限大的.正是因为这个怪圈具有一些奇异的性质而成为数学珍品之一.在生活中莫比乌斯带也发挥着无可比拟的作用.
在生活中,如果巧妙地运用这个“怪圈”,那它的力量是必深不可测.我们常见的普通传动都带有两个面,平时操作时只能用到一面,很多了解过莫比乌斯带的人就考虑用莫比乌斯环来做传动带,因为它具有单侧性,在使用时损耗就相对较平均了,从而可延长传送带的使用寿命,提高利用率.实验证明,用莫比乌斯带做的传送带性价比和实用性都高于普通传送带.认识了莫比乌斯带,就会发现游乐场的轨道也是如此.还有一些人常常模拟蚂蚁在莫比乌斯圈循环上往复行走来证明它的几何特征,它蕴含着永恒、无限的意义,因此,常被人们用于设计各类有意义的标志.包括垃圾可循环的标志,留心观察正是莫比乌斯带,它所赋予的伟大力量还需要年轻的我们不断发掘,不断创造.
当然,大学期间的数学学习虽严谨,但正缺少这种趣味性学习和思考,也缺少数学的应用意识和创新.这也难怪很多学生学完每学期的课程后,基本忘得差不多.我想如果打破传统的数学被动认知教学,对学生的数学理解会不会更有帮助.就像数学分析,刚开始学很零散.学完就会发现,它是将极限这条线把一颗颗零散的珍惜串起来,它们是在实数集的范围内以极限的思想思考问题.大学生在刚接触一些高等数学时难免会吃力.在一些难以理解的内容上,以学生的角度,如果教师加上一些很形象的动图——以极限为例,或者一些数学家在思索这个规律的一些人物故事——以牛顿莱布尼兹公式为例.牛顿莱布尼兹公式的命名正所谓是一波三折,数学书上的昙花一现,可是花了十几世纪,多少数学家的争论才得来的,实属不易,他们智慧而伟大,令人敬仰.包括印度数学家拉马努金,他对代数公式,无穷级数的变换能力惊人惊讶,可天妒英才,他在剑桥学习也仅仅几年,却病逝而终!但他留给后代的数学知识却是永恒的.因此,我们要尊重每一个数学公式、数学定理,每一位数学家,他们平凡而伟大.
我所谈及的也不过是数学中的冰山一角,数学的魅力远远不止这些,作为新时代的大学生,我们要持之以恒地深造自身专业素养.数学的魅力是无穷无尽的,只要你愿意去钻研总会感受到它的力量.生活中还有很多值得我们思考的数学,类似清华学霸用微积分证明的薯片相切可吃定理,希望这些数学可以启发我们每一个人的思维,用数学的眼光看问题、解决问题,用数学的思维研究问题,学习数学家身上的精神.将数学思维方法和数学家们的钻研精神铭记在心,不断鞭策自己前行!这些让我感同身受的数学魅力,希望也同样能启迪到热爱数学的你!
参考文献
[1] 邵倩.语域理论视角下的“禅师体”特征探析[J].太原大学学报,2013(2):68-70.