
0 引言
房地产业在国民经济中起着举足轻重的作用,它牵动着相关产业的发展,同时也蕴含着巨大的金融和社会问题,房地产业一直是一个研究热点.在房地产市场中,房价是房地产市场的外在表现,它是诸多因素影响的结果,因此房地产市场的供需是否平衡,结构是否合理,行业是否稳定,可持续发展是否健康,这些都引起了广大学者的关注和研究.国家政府出台很多政策来保障市场的稳定.但是由于一方面房价远远超出大多数居民的支付能力,另一方面公共住房的建设又由于资金链中断等原因供应量非常有限,居民自有住房需求远不能满足,各地普遍存在结构性供需严重不平衡的状况,这不仅导致社会资源的严重浪费;同时在这种严重的不平衡结构下,由于房地产资金过度依赖银行贷款,隐含着严重的金融危机;再者房地产供需不平衡,还会带来由于房地产投资过热而形成严重的资产泡沫问题,从而进一步引发经济危机.本文运用直觉模糊数和博弈论的知识建立了开发商之间的矩阵博弈模型并求解,为开发商投资的开发项目方案提供了理论依据,从而避免开发商盲目投资,降低经济危机的风险.
1 开发商之间的博弈模型
1.1 模型建立的背景
博弈论是研究决策主体的行为在发生相互作用时,人们如何进行决策以及这种决策的均衡问题,即假设局中人是理性人,选择相应策略是自己的支付达到最大.在房地产市场中,在各个房地产市场主体之间存在多个博弈模型.同时房地产市场是一个模糊系统,影响房地产市场稳定的诸多因素在相互关系、作用程度、数据收集方面均符合模糊系统的概念,与此同时由于社会经济市场环境的日益复杂性和不确定性,各种风险的存在下市场主体在做决策过程中,往往存在着不同程度的犹豫或表现出一定程度的知识缺乏,从而使得决策结果表现为肯定、否定或介于肯定和否定之间的犹豫性.直觉模糊信息集成理论正是研究这种带有犹豫度的模糊系统,即直觉模糊集同时考虑了隶属度、非隶属度和犹豫度这三个方面的信息.在房地产市场中,房地产市场主体主要有开发商、政府,消费者三个,本文主要研究开发商之间的博弈,开发商主要以追求利益最大化为目标,为市场占有率为最大目标.
为了更好更完整的说明首先介绍一下住宅房屋的特点 和 性 质 ,2011 年 修 订 的《 住 宅 设 计 规 范 》(GB50096-2011)规定:住宅(residential buildings),指供家庭居住使用的建筑.住宅是指专供居住的房屋,包括别墅、公寓、职工家属宿舍和集体宿舍、职工单身宿舍和学生宿舍等,但不包括住宅楼中作为人防用、不住人的地下室等,也不包括托儿所、病房、疗养院、旅馆等具有专门用途的房屋,按产品性质分类:普通住宅,别墅,公寓,花园洋房,经济适用房.
普通住宅,是指按所在地一般民用住宅建筑标准建造的居住用房屋.目前,多为多层住宅和高层住宅,多层住宅是指2-6层(含6层)的楼房;高层住宅是指6层以上的楼房,高层住宅多安装电梯,现在这个寸金寸土的时代,小高层有多层亲切安宁、房型好、得房率高的特点,又有普通高层结构强度高、耐用年限高、景观系数高,污染程度低等优点,很受购房人欢迎.同时,小高层对土地的利用率提高,土地成本相对下降,投资利润大,风险相对较小很受房地产开发商的青睐,所以,近年来中心城区小高层如雨后春笋,越来越多.
国土资源部对别墅的定义:是指独门独户独院,两至三层楼形式;占地面积又相当大,容积率又非常低.而土地资源的不可再生,决定了别墅产品相对其它住宅产品而言,更能保值增值.同时投资别墅的利润高,但别墅的需求是有限的,风险也就相对较高.
经济适用住房是指已经列入国家计划,由城市政府组织房地产开发企业或者集资建房单位建造,以微利价向城镇中低收入家庭出售的住房.它是具有社会保障性质的商品住宅.1994年由建设部、国务院房改领导小组、财政部联合发布的《城镇经济适用住房建设管理办法》指出,经济适用住房是以中低收入家庭、住房困难户为供应对象,并按国家、住宅建设标准(不含别墅、高级公寓、外销住宅)建设的普通住宅,这种住房成本低,开发商没有权利更改房(限价房),同时经济适用房项目大部分均位于城乡结合地区,交通不便,购买者需符合要求才能购买,房屋空置率不高,但利润小.
1.2 矩阵博弈的建立
基于以上假设和分析,在房地产开发商博弈中,设局中人是开发商甲、乙;策略集是开发项目方案,其中开发商甲有 m 个方案,乙有 n 个方案.由于双方不进行价格之争,故以双方占领市场的相对可能性作为对策的支付值.每一个开发商投资时都会以往年市场的房地产的销售情况作为参考并且结合当前政策进行开发和投资,但是开发商在投资过程中都是有个人风险偏好,同时也会考虑一定的社会风险因素,考虑到数据的可获得性以及可预测性,本文以往年各类房地产项目类型的市场占有的相对可能性作为开发商甲的支付值,以销售率和风险系数的乘积作为犹豫参数建立模型,如图1所示:
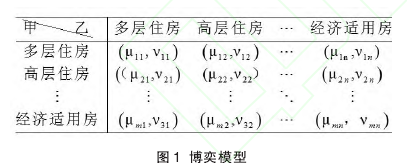
其中 μ11是近年来一类住宅销售面积数/所有商品房总得销售面积数,即表示开发商甲和开发商乙同时投资这类住房时,开发商甲可能占有市场的最小可能性;用字母ω 表示近年来这类住宅的销售面积/这类住宅的开发面积,γ 是房地产开发商的投资风险系数,即 ωγ 就是开发商甲的投资犹豫系数;ν11=1-μ11-ωγ 表示此时甲不能占有市场的最大可能性.
1.3 模型的求解
在经典矩阵对策的求解过程中,每个局中人获得的支付的多少不仅取决于自己所采取的策略,还受其他人采取策略的影响,这样每个局中人都需要针对对方的策略选择做出对自己最有利的反应对策.因此假定局中人是理性的,遵循“从最坏处着想,从最好处入手”的对策原则,即局中人甲选取混合策略 x 使其期望支付值 E(x,y)=(x^T)A y 最大,而局中人乙则选取混合策略 y 使其期望支付值E(x,y) = (x^T)A y 最小,即局中人甲按照最大最小准则选取策略,局中人乙按照最小最大准则选取策略.但是在直觉模糊集矩阵对策中由于开发商的支付值是带有两标度(隶属度和非隶属度)的直觉模糊集,所以在求解时就是将转换为双目标线性规划,即目标函数开发商甲的最小赢得为:
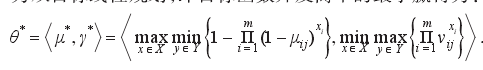
而求解多目标线性规划通常用到Pareto最优解的概念,进一 步 根 据 线 性 加 权 方 法 将 目 标 函 数 变 为min{ λμ* +(1-λ)ν*} ,λ∈[0,1]是偏好权重.通过一系列的数学变换进一步转为下面非线性规划,其中 λ∈[0.1]
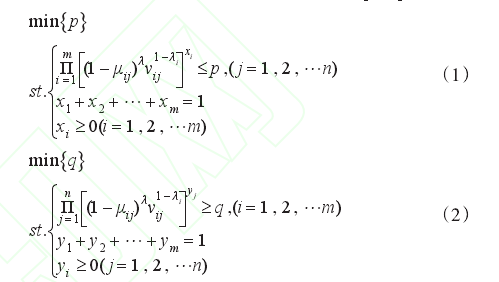
则式(1)和式(2)得到解 (x*,p*)和(y*,q*) 即为直觉模糊集矩阵对策的最优策略,此时开发商甲和乙达到市场占有相对可能性的均衡.
2 实例分析
《2009年浙江房地产市场形势分析》一文中认为2009年浙江房地产市场仍将处于调整期,指出房地产融资环境较紧,市场环境是供大于求,在这样的环境中开发商该怎么样投资才能保证降低风险的基础上实现自己的利益最大化,下列本文就以浙江省为例,具体说明.根据需要假设条件:
假定1:各个参与者(即开发商)都是理性人;假定2:开发商之间竞争的是市场占有率,而非价格之争;假定3:某地区只有两个开发商,且每个开发商的能力是相同的;假定4:开发商项目定位在住房,市场需求是稳定的.
在假设的条件下,我们根据近年来浙江省的新开工的房屋面积和销售情况做出分析.
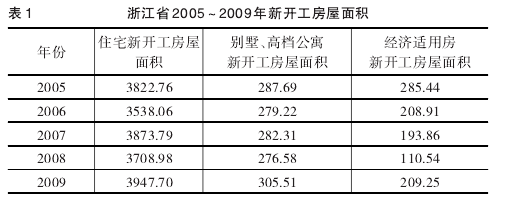
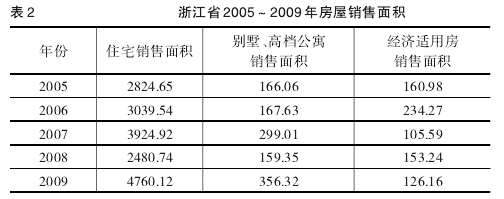
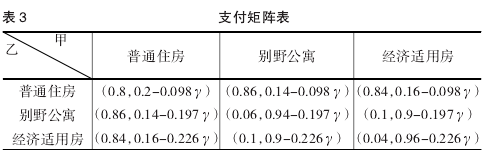
根据以上分析结果和表格数据我们得到支付矩阵见表3所示.
则直觉模糊集混合策略矩阵为.

其中 γ 是风险系数,但是由于直觉模糊集信息集成理论中有隶属度和非隶属度之和是小于等于 1,所以0.84 + 0.16 - 0.226γ ∈ 1 和 0.86 + 0.14 - 0.197γ ∈ 1 有 γ ∈0.701 .
根据式(1)和式(2)得到两个非线性规划模型,运用lingo和matlab软件求得不同情况下的均衡策略最优解如表4所示.

结果说明:当 γ=0.7,λ=0.9时 ,开发商按照(0.90520.0948 0)的比例混合使用三个策略,乙开发商按照(0.7063,0,0.2937)的比例混合使用三个策略时,矩阵对策达到均衡.开发商甲占领市场的最小可能性为0.7952;不能够占领市场的最大可能性为 0.1297;不确定指数为0.0751.表格4中的其他结果可做类似地解释.
3 结论
本文针对房地产市场开发商之间展开的占有市场竞争进行了博弈均衡分析,找到了基于不同风险系数和投资偏好时的投资均衡策略,为房地产项目投资提供科学而符合实际情况的决策.本文认为,在开发商互相联盟不进行价格竞争的情况下,研究其开发方案之间的竞争可以降低房屋的空置率,可以缓解供求不平衡的困境.同时,在博弈过程中,发现市场占有的相对可能性是权重系数和风险系数共同作用的具体投资方案可以参考表(4).开发商投资时不能盲目,要知己知彼,才能使利益达到最大化的同时保证房地产市场的可持续发展.
参考文献:
[1]李晓娟.房地产投资项目的风险厌恶博弈及其应用[J].湖南大学学报(社会科学报),2012,26(4).
[2]虞晓芬.2009年浙江房地产市场形势分析[J].浙江统计,2009,(2).
[3]王进,李准,曹升元,基于博弈论的房地产开发商行为决策研究[J].建筑经济,2007,(6).
[4]刘文,王骏,王晓银.基于多角度的我国房地产行业数学模型的建立与分析[J].数学的实践与认识,2012,15(42).
[5]陈创泉,林慧欣,欧温暖,房少梅.基于房地产行业发展现状的数学模型[J].数学的实践与认识,2012,15(42).
[6]Li Deng-feng, Nan Jiang-xia. A Nonlinear Programming Approach toMatrix Games with Payoffs of Atanassov's Intuitionistic Fuzzy Sets[J].Int J. of Uncertainty, Fuzziness and Knowledge-based Systems, 2009.





