
1、 引言
中介变量(mediator)在心理、教育、社会和管理等研究中扮演着重要的角色。如果自变量 X 通过某一变量 M 对因变量 Y 产生一定影响,则称 M 为 X和 Y 的中介变量或 M 在 X 和 Y 之间起中介作用(如图 1 所示,其中的圆圈表示变量可以是显变量或潜变量)。中介研究的意义在于帮助我们解释自变量和因变量关系的作用机制,也可以整合已有变量之间的关系(罗胜强,姜嬿,2012; 温忠麟,刘红云,侯杰泰,2012; MacKinnon,2008)。
在心理、行为和其它一些社科研究领域,研究情境复杂,经常需要多个中介变量才能更清晰地解释自变量对因变量的效应(Mackinnon,2008)。近年来,越来越多的中介研究采用多重中介(multiple me-diation) 模型。不过,多数研究是将一个多重中介模型拆解为多个简单中介(即只含一个中介变量)模型,相继进行多个简单中介分析。建立结构方程模型(Structural Equation Model,SEM)进行多重中介分析,不仅可以同时处理显变量和潜变量,还可以同时分析多个自变量、多个因变量和多个中介变量的关系,是比较好的方法。本文探讨如何正确地利用SEM 进行多重中介效应分析。在简介多重中介效应模型后,讨论了多重中介模型的 SEM 分析现状及存在的问题;接着,总结出一套多重中介效应的 SEM分析方法;然后,用一个例子说明如何进行多重中介效应的 SEM 分析,并给出了 MPLUS 和 LISREL 程序;最后对相关问题进行了讨论和拓展。
2、 多重中介模型
多重中介模型即存在多个中介变量的模型。根据多个中介变量之间是否存在相互影响,多重中介模型可以分为单步多重中介模型(single - step mul-tiple mediator model) 和多步多重中介模型( multiple- step multiple mediator model) ( Hayes,2009 ) 。单步多重中介模型是指多个中介变量之间不存在相互影响(图 2 中去掉 M1→M2路径便是一个单步多重中介模型),又称为并行多重中介模型。多步多重中介模型是指多个中介变量之间存在相互影响,多个中介变量表现出顺序性特征,形成中介链(如图 2 中的 X→M1→M2→Y路径),又称为链式多重中介模型(柳士顺,凌文辁,2009)。

以图 2 所示的含有两个中介变量 M1和 M2的多重中介模型为例(其中的圆圈表示变量可以是显变量或潜变量),此时的多重中介效应分析可以从三个角度进行,(1)特定路径的中介效应(specific mediationeffect),如 a1b1、a2b2和 a1a3b2,(2)总的中介效应(total mediation effect),即 a1b1+ a2b2+ a1a3b2,(3)对比中介效应,如 a1a3b2- a2b2、a1b1- a2b2和 a1a3b2- a1b1( 柳 士 顺,凌 文 辁,2009; Hayes,2009;MacKinnon,2008; Preacher & Hayes,2008) 。
多重中介模型相对于简单中介模型具有三大优势。首先,可以得到总的中介效应。其次,可以在控制其他中介变量(如控制 M1)的前提下,研究每个中介变量(如 M2)的特定中介效应。这种做法可以减少简单中介模型因为忽略其他中介变量而导致的参数估计偏差。第三,可以得到对比中介效应,使得研究者能判断多个中介变量的效应(如 a1b1和 a2b2)中,哪一个效应更大,即判断哪一个中介变量的作用更强。这样,对比中介效应能使研究者判断多个中介变量理论(如 X→M1→Y和 X→ M2→Y)中,哪个中介变量理论更有意义。因此研究多重中介模型更具理论和实践意义(Preacher & Hayes,2008)。
3 多重中介模型的 SEM 分析现状目前大多数研究者在利用结构方程模型进行多重中介分析时,往往只从某个角度分析了多重中介效应。例如,使用 LISREL 软件进行多重中介分析时,大多数研究者会在输出指令“OU”中加入“EF”选项,只能得到总的中介效应估计值及其标准误和 t值(邱皓政,林碧芳,2009; 温忠麟,张雷,侯杰泰,刘红云,2004);使用 AMOS 软件进行多重中介分析时,大多数研究者会在分析属性(Analysis Proper-ties)→结果(Output)对话框中击选“indirect,direct& total effects”选项,也只能得到总的中介效应估计值(李茂能,2011; Cheung & Lau,2008; Lau &Cheung,2012; Preacher & Hayes, 2008 ) ; 使 用MPLUS 软件进行多重中介分析时,大多数研究者会使用“MODEL INDIRECT”命令,可以得到特定路径的中介效应和总的中介效应估计值,但还是得不到对比中介效应的分析结果(邱皓政,林碧芳,2009;王济川,王小倩,姜宝法,2011; Cheung,2007;Muthén & Muthén,2010;Preacher & Hayes,2008)。
另外,大多数研究者常用结构方程软件默认的中介分析方法进行中介效应检验,例如 LISREL、A-MOS 和 MPLUS 软件都默认使用 Sobel 检验来判断中介效应是否显著(邱皓政,林碧芳,2009)。但现有研究发现,即使在简单中介效应检验中,Sobel 检验都有局限(方杰,张敏强,邱皓政,2012; Hayes,2009; Mackinnon,2008)。在多重中介模型中,Sobel检验的局限有增无减。首先,Sobel 检验统计量的推导基于正态假设,而特定中介效应、总的中介效应和对比中介效应估计值都涉及参数的乘积,因而通常都不满足正态假设,因此 Sobel 检验的结果是不准确的,检验力不高。其次,Sobel 检验需要大样本,Sobel检验在小样本的表现并不好。第三,在多重中介模型中,Sobel 检验统计量公式的分母是中介效应估计值的标准误,而这个标准误常用多元 delta 法(multi-variate delta method) 计算,公式十分复杂 ( 邱皓政,林碧芳,2009; MacKinnon,2008; Taylor,MacKin-non,& Tein,2008 ),且需要手工计算,使用不便(Cheung,2007; Macho & Ledermann,2011)。截至目前,国内研究者仅有刘亚(2012) 使用多元 delta法,手工计算了神经质→情绪→自尊→生活满意度的链式多重中介的标准误。
综上所述,目前多重中介效应分析的存在问题包括:(1)分析不完整;(2)使用 Sobel 检验的局限;(3)Sobel 检验统计量计算复杂,且需要手工计算。
4、 多重中介效应的 SEM 分析方法
针对上述多重中介效应分析中已存在的各种问题,方法学研究者从不同角度提出了各自的解决办法。本文要做的是综合利用各种方法,试图总结出一套能一举解决全部三个存在问题的方法,为应用研究者在进行多重中介分析时提供有益的参考。
4. 1 增加辅助变量进行完整多重中介效应分析
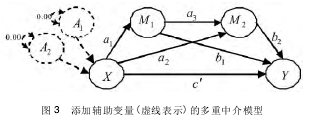
针对当前多重中介效应分析不完整的问题,Cheung(2007)提出在结构方程模型中加入辅助变量(auxiliary variable)的方法可以进行完整的多重中介效应分析。辅助变量是一个方差为 0 的潜变量(见图 3 中的虚线圆圈)。由于辅助变量的方差为 0,因此多重中介模型中新增加的辅助变量不会影响原有参数的估计值和模型的拟合程度,所以辅助变量又被称为幽灵变量(phantom variable)(李茂能,2011;叶宝娟,温忠麟,2012; Cheung,2007; Macho & Le-dermann,2011)。Cheung(2007)将没有任何实质意义的辅助变量加入模型中,目的仅在于通过非线性约束(nonlinear constraint)来进行中介效应估计。具体地说,将辅助变量作为自变量的预测变量(见图3),此时的回归系数(即辅助变量到自变量的路径系数)被约束为研究者想得到的中介效应值。在同一个结构方程模型中,可以同时增加多个辅助变量(见图 3 中的 A1和 A2。例如,LISREL 软件只需要在输入指令“DA”的结尾处加入“AP”选项(李茂能,2011; Cheung,2007),MPLUS 软件只需使用“MOD-EL CONSTRAINT”命令( Muthén & Muthén,2010),就可以便利的设置多个辅助变量。这样,通过设置多个辅助变量,使得研究者可以同时得到特定、总的和对比中介效应值,实现完整的多重中介效应分析。
4. 2 多重中介分析的 Bootstrap 方法
通过增设辅助变量(解决了分析不完整的问题),结构方程软件(例如 LISREL 和 MPLUS)会自动输出中介效应的估计值、相应的标准误和 t 值,根据这些信息就可以判断中介效应的显著性了(解决了Sobel 检验统计量计算复杂,且需要手工计算的问题)。但是,Sobel 检验需要正态性、大样本的问题还没有得到解决。解决的办法是彻底弃用 Sobel 检验法,改用 Bootstrap 方法,因为 Bootstrap 方法即不需要正态性假设,也不需要大样本,进行中介效应区间(如果区间不包括 0,表示中介效应显著)估计时更无需标准误。
Bootstrap 方法是由 Efron 最早提出的一种重复抽样方法(resampling methods)。Bootstrap 方法是将原始样本当成 Bootstrap 抽样的总体,通过有放回的重复抽样,抽取大量 Bootstrap 样本并获得统计量的过程,其实质是模拟了从总体中随机抽取大量样本的过程。Bootstrap 方法的唯一要求是原始样本可以反映研究总体,但不需要知道研究总体的具体分布。常用的 Bootstrap 方法包括百分位 Bootstrap 方法(Percentile Bootstrap Method)和偏差校正的(Bias -Corrected)百分位 Bootstrap 方法。有关 Bootstrap 方法的具体步骤,请参阅相关文献(方杰,张敏强,李晓鹏,2011; 温忠麟等,2012)。
Cheung(2007)模拟比较了在增加辅助变量的前提下,Bootstrap 方法和 Sobel 检验法在链式多重中介a1a3b2和对比多重中介 a1b1- a2b2(见图 3)分析中的表现,发现当中介效应值和样本量都很小的情况下,Bootstrap 方法明显优于 Sobel 检验法,这和其他研究的结果一致(参见方杰等,2011)。大量的研究还表明,偏差校正的百分位 Bootstrap 方法优于百分位 Bootstrap 方法(方杰等,2011),因此推荐研究者使用偏差校正的百分位 Bootstrap 方法进行中介效应分析。Cheung 和 Law(2008)指出使用偏差校正的百分位 Bootstrap 方法需要注意两点,一个是至少抽取 1000 以上的 Bootstrap 样本,以确保结果的一致性和稳定性;二是利用交叉验证(cross validate)的方法,即利用百分位 Bootstrap 方法良好的第Ⅰ类错误率表现来控制偏差校正的百分位 Bootstrap 方法可能高估第Ⅰ类错误率的问题。
目前,SEM 分析软件比较常用的有三种:A-MOS、MPLUS 和 LISREL。AMOS 软件在分析属性(Analysis Properties)→Bootstrap对话框就可以进行Bootstrap 方法的设置,但是 AMOS 软件无法同时提供辅助变量的设置。MPLUS 软件在“ANALYSIS”命令中就可以进行 Bootstrap 方法的设置,也能设置多个辅助变量,因此能使用 Bootstrap 方法进行完整的多重中介分析(Muthén & Muthén,2010)。但是 Lau和 Cheung(2012)指出,由于 MPLUS 软件不允许将所有内生潜变量(endogenous latent variable)的方差约束成一样,因此不能给出多重中介效应的标准化解,使用 LISREL 软件进行 Bootstrap 分析才能得到多重中介效应的标准化解。
LISREL 软件进行 Bootstrap 分析的步骤分为六步(程序见附录 1)。
第一步,使用 LISREL 软件中的 PRELIS 程序从原始样本中抽取至少 1000 个 Bootstrap 样本。
第二步,设置辅助变量,采用固定方差法编写可以分析多个样本的 LISREL 程序(如果采用固定负荷法编写 LISREL 程序将得到中介效应的非标准化解)。
第三步,运行 LISREL 程序分析 1000 个 Boot-strap 样本,得到研究者感兴趣的特定、总的和对比中介效应系数估计值各 1000 个,保存为 PRELIS 数据文件(* . psf)。
第四步,将 PRELIS 数据文件导出为 EXCEL 文件(* . xls)。
第五步,在 EXCEL 中将 1000 个中介效应估计值从小到大进行排序,将 1000 个中介效应估计值的均值作为中介效应估计值的标准化解;用第 2. 5 百分位数和第 97. 5 百分位数来估计 95% 的中介效应置信区间,如果置信区间不包括 0,说明中介效应显著,百分位 Bootstrap 方法的中介效应检验完成。
第六步,对第五步得到的中介效应置信区间进行校正,得到偏差校正的百分位 Bootstrap 方法的中介效应置信区间,如果置信区间不包括 0,说明中介效应显著,偏差校正的百分位 Bootstrap 方法的中介效应检验完成(温忠麟等,2012; Lau & Cheung,2012) 。
如上所述,三种主流结构方程软件在利用 Boot-strap 方法进行多重中介效应分析时,各有利弊。A-MOS 软件的优点是方便实施 Bootstrap 方法,缺点是无法设置辅助变量;MPLUS 软件的优点是方便实施Bootstrap 方法,能设置辅助变量,缺点是无法得到中介效应标准化解;LISREL 软件的优点是能设置辅助变量,可以得到中介效应标准化解,缺点是执行Bootstrap 方法的步骤比较繁琐。应用研究者可以根据自己的研究需要和对软件的熟悉程度对软件进行选择。
4. 3 多重中介效应的 SEM 分析流程
面对一个多重中介效应分析任务,研究者应当如何进行呢? 根据前面的讨论,我们总结出一个多重中介效应的 SEM 分析流程如下:
1. 确定多重中介模型。由于中介模型是一种验证性模型而不是探索性模型,因此必须首先根据理论确定自变量、中介变量和因变量,以及变量之间的因果顺序。
2. 设置辅助变量。根据第 1 步确立的多重中介模型和使用的 SEM 软件,设置相应的辅助变量。
3. 偏差校正 Bootstrap 的 SEM 分析。如果 SEM模型的拟合程度可接受,则根据偏差校正 Bootstrap得到的中介效应区间估计进行中介效应显著性判断(判断方法是,对要检验的中介效应(如特定中介效应),如果其置信区间不包含零,则相应的中介效应显著);如果 SEM 模型的拟合程度不可接受,则停止分析。
5、 多重中介模型的 SEM 分析示例。
接下来用一个实际例子演示如何用多重中介效应的 SEM 分析流程检验多重中介效应。本例要研究的是(积极和消极)应对方式( M1和 M2)对初中生感戴状况(X)与学校生活满意度(Y)关系的并行多重中介效应(见图 4)。变量及其数据(839 人)均来自孙配贞等人的研究(孙配贞,郑雪,余祖伟,2010)。采用 MPLUS6. 0 软件进行并行多重中介效应分析,由于“MODEL INDIRECT”命令无法得到对比中介效应 a1b1- a2b2,因此将其设置为辅助变量。使用偏差校正的 Bootstrap 方法进行分析(MPLUS 程序见附录 2)。
首先需要检验模型的拟合程度。MPLUS 软件得到的模型拟合结果是 χ2= 156. 29,自由度 df =32,χ2/ df = 4. 88,CFI = . 96,TLI = . 94,RMSEA =. 07,模型拟合程度良好。偏差校正的 Bootstrap 方法对并行多重中介效应(见图 4)的分析结果见表 1。
结果显示,(积极和消极)应对方式( M1和 M2)的特定中介效应都显著,总的中介效应也显著,但两个特定中介效应之间的差异不显著,表明积极应对和消极应对的中介效应相当。另外,由于对比中介效应设置为辅助变量,因此只能得到对比中介效应的非标准化解。

6 、小结与讨论
针对当前多重中介效应的 SEM 分析中存在的多重中介效应分析不完整和常用中介分析 Sobel 检验法有局限等问题,本文建议通过增加辅助变量的方法进行完整的多重中介效应分析,并使用不需要以正态性、大样本作为前提假设的 Bootstrap 方法进行检验。我们总结出一个多重中介效应分析的 SEM流程,并通过一个例子演示了如何进行多重中介效应的 SEM 分析。但是,本文仍然存在一些不足,尚需进一步深入讨论和拓展。
6. 1 辅助变量
本文使用辅助变量进行完整的多重中介分析,但这并不是唯一的方法。Preacher 和 Hays(2008)提出利用似然比(Likelihood Ratio,LR)检验的方法执行对比中介效应 a1b1- a2b2检验。似然比检验的原理是,首先产生一个约束模型,即在原模型的基础上增加一个非线性约束(a1b1= a2b2);然后对原模型和约束模型的 χ2值的差异 Δχ2进行检验,如果Δχ2达到统计上的显著程度,就表示 a1b1和 a2b2的大小存在显著差异。Preacher 和 Hays(2008)指出似然比检验法与 Sobel 检验法会得到相似的结论,Lau 和Cheung(2012) 使用偏差校正的 Bootstrap 方法和似然比检验法对同一数据进行多重中介效应分析,也发现结果一致。但是,似然比检验法仍然存在两个问题。Preacher 和 Hays(2008)明确指出,似然比检验法在多重中介效应中的表现没有通过模拟研究进行考察,因此仅凭几个实例分析结果还不能对似然比检验法在多重中介效应中的表现做出令人信服的结论。Lau 和 Cheung(2012)也指出,似然比检验法与提供区间估计的方法(Bootstrap 和贝叶斯方法)相比,存在信息量少的缺点,例如似然比检验法只能给出显著性 p 值,无法给出标准误。
Macho 和 Ledermann(2011) 认为辅助变量法仍然存在不足。第一,具备强大图形界面功能的 A-MOS 软件不能执行辅助变量所要求的非线性约束,因此难以使用 Bootstrap 法进行完整的多重中介分析。第二,如果模型十分复杂,在多重中介效应分析中需要检验的代数表达式也会比较复杂,容易出错。
因此 Macho 和 Ledermann 提出幽灵模型法(phantommodel approach)进行极复杂模型的多重中介效应分析。幽灵模型法无需用代数表达式来表示研究者感兴趣的中介效应大小,也就无需辅助变量进行非线性约束。幽灵模型法的原理是将研究者感兴趣的中介效应表征为幽灵模型总的中介效应。幽灵模型可以通过对主模型(main model,即包含所有变量和所有路径的模型)进行约束得到。值得注意的是,幽灵模型法也不能得到中介效应的标准化解。
6. 2 其他方法介绍
本文涉及的 Sobel 检验和 Bootstrap 法都属于频率统计(frequentist statistic) 的范畴。贝叶斯方法(Bayesian method) 是和频率统计相对应的统计方法。二者的区别主要在于,频率统计将待估参数(例如中介效应值)看成是一个常数,而贝叶斯方法则将待估参数看成是一个变量(李锡钦,2011; Muthén,2010; Muthén & Asparouhov,2012)。贝叶斯方法是结合研究者在数据未收集之前对于待估参数的先验信息(prior information) 与来自观测数据的似然函数,以获得待估参数的后验分布(描述待估参数取值的概率分布和可靠程度),再进行统计推论的数据分析方法。贝叶斯方法同样具有无需正态性假设,不需要大样本,中介效应区间估计时无需标准误的优点。近年来,由于马尔科夫链蒙特卡罗 (Markovchain Monte Carlo,MCMC) 算法( 可得到待估参数的后验分布)的成功实现,使得贝叶斯方法便利地应用到中介分析等领域中。有关使用马尔科夫链蒙特卡罗算法执行贝叶斯方法的具体步骤,请参阅相关文献(方杰等,2011)。目前,多款结构方程软件(如AMOS 和 MPLUS 的 6. 0 以上版本) 都可以使用贝叶斯 SEM 方法进行中介效应分析(都只能得到中介效应的非标准化解)。贝叶斯 SEM 方法进行多重中介分析的具体例子,可参见李茂能(2011)。但是,贝叶斯方法仍处在发展阶段,还存在一些函待解决的问题。例如,贝叶斯方法的一大优势是将先验信息整合到中介效应分析中,从而得到更准确的中介效应点估计和区间估计,然而如何获得先验信息呢? 目前学界仍在讨论中,尚无定论。又如,已有研究发现,无先验信息的贝叶斯方法和 Bootstrap 法的中介效应分析结果十分相近(方杰,张敏强,2012; 李茂能,2011; Biesanz,Falk,& Savalei,2010; Yuan &MacKinnon,2009),优势并不明显。
另外,本文涉及的 Sobel 检验和 Bootstrap 法都属于使用系数乘积(products of coefficients)进行中介效应检验的类型,实际上还有另外两类中介效应检验方法,包括依次检验法和系数差异法(differencein coefficients)。但依次检验法不适用于检验对比中介;至于系数差异法,在简单中介模型中的表现就不好(方杰,张敏强,邱皓政,2012),因此这两种方法不在本文的讨论范围之内。
第三,Bootstrap 法和贝叶斯方法虽然都适用于小样本,但是测量工具(量表) 的信效度与样本大小、样本代表性仍然会严重影响参数的正确估计。
尤其是原始样本如果太小或不具有代表性,不管是Bootstrap 法或贝叶斯方法都无法有效改善参数估计的正确性(李茂能,2011)。那么,在确保统计功效足够大(常用 . 8)的前提下,原始样本最少需要多少样本量呢? Fritz 和 Mackinnon(2007)用模拟研究比较了统计功效为 . 8 时,Sobel 法和 Bootstrap 法在简单中介分析中所需样本量的情况,但是没有涉及贝叶斯方法,也没有涉及多重中介模型。统计功效为. 8 时,多重中介效应分析中,Bootstrap 和贝叶斯法所需样本量的情况是一个具有显著实际意义的课题。
以中国期刊网全文数据库为数据源进行搜索,截止 2013 年 1 月 1 日,国内心理学期刊仅有 10 篇利用 Bootstrap 方法进行中介效应分析的应用研究,其中使用 SEM 软件进行潜变量的多重中介效应分析的应用研究仅有 2 篇(尤方华,陈志霞,2012; 赵晶晶,孔风,王勇惠,2012),还未发现使用贝叶斯方法进行中介效应分析的应用研究。希望本文能起到抛砖引玉的作用,相信随着多重中介效应研究的深入,会不断增加我们对多重中介问题的理解,更全面、有效的挖掘数据中的信息,特别是对比中介效应的信息,使得心理学的研究方法更具有解释力。
参考文献:
1.方杰,张敏强. (2012). 中介效应的点估计和区间估计: 乘积分布法、非参数 Bootstrap 和 MCMC 法. 心理学报,44 ,1408 – 1420.
2.方杰,张敏强,李晓鹏. (2011). 中介效应的三类区间估计方法. 心理科学进展,19 ,765 – 774.
3.方杰,张敏强,邱皓政. (2012). 中介效应的检验方法和效果量测量: 回顾与展望. 心理发展与教育,28 ,105 – 111.
4.李茂能. (2011). 图解AMOS 在学术研究中的应用. 重庆: 重庆大学出版社.
5.李锡钦. (2011). 结构方程模型: 贝叶斯方法 (蔡敬衡,潘俊豪,周影辉译). 北京: 高等教育出版社.
6.柳士顺,凌文辁. (2009). 多重中介模型及其应用. 心理科学,32 ,433 – 435.
7.刘亚. (2012). 神经质与生活满意度的关系: 情绪和自尊的链式中介作用. 心理科学,35 ,1254 – 1260.
8.罗胜强,姜嬿. (2012). 调节变量和中介变量. 组织与管理研究的实证方法. 北京: 北京大学出版社.
9.邱皓政,林碧芳. (2009). 结构方程模型的原理与应用. 北京: 中国轻工业出版社.
10.孙配贞,郑雪,余祖伟. (2010). 初中生感戴状况与学校生活满意度的关系: 应对方式的中介作用. 心理发展与教育,26 ,67 –72.
11.王济川,王小倩,姜宝法. (2011). 结构方程模型: 方法与应用. 北京: 高等教育出版社.





